快速傅里叶变换FFT：效率提升与算法解析

"快速傅里叶变换(FFT)是离散傅里叶变换(DFT)的一种高效算法，主要分为时间抽取法和频率抽取法，通常适用于序列长度为2的幂的情况。此外，还存在组合数基四FFT算法来处理一般长度的序列。FFT通过巧妙的分解和重排计算，显著减少了所需的复数乘法和加法次数，从而提高了计算速度。" 在数字信号处理和许多其他领域，快速傅里叶变换(FFT)是计算离散傅里叶变换(DFT)的关键工具，因为其极大地降低了计算复杂性。DFT对于分析周期性和非周期性信号的频谱特性至关重要，但其直接计算方式需要大量的计算资源。当处理大数据量时，直接方法的效率非常低。 首先，我们来看DFT的运算量。给定一个长度为N的复数序列x(n)，其DFT定义为： \[ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j2\pi kn/N} \] 反向的逆离散傅里叶变换(IDFT)则是： \[ x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \cdot e^{j2\pi kn/N} \] 对于复数乘法和加法，计算机实现时通常需要四个实数乘法和两个实数加法来完成一个复数乘法，以及两个实数加法来完成一个复数加法。如果直接计算N点的DFT，那么需要\( N^2 \)次复数乘法和\( N(N-1) \)次复数加法。这在计算大N值时变得非常耗时。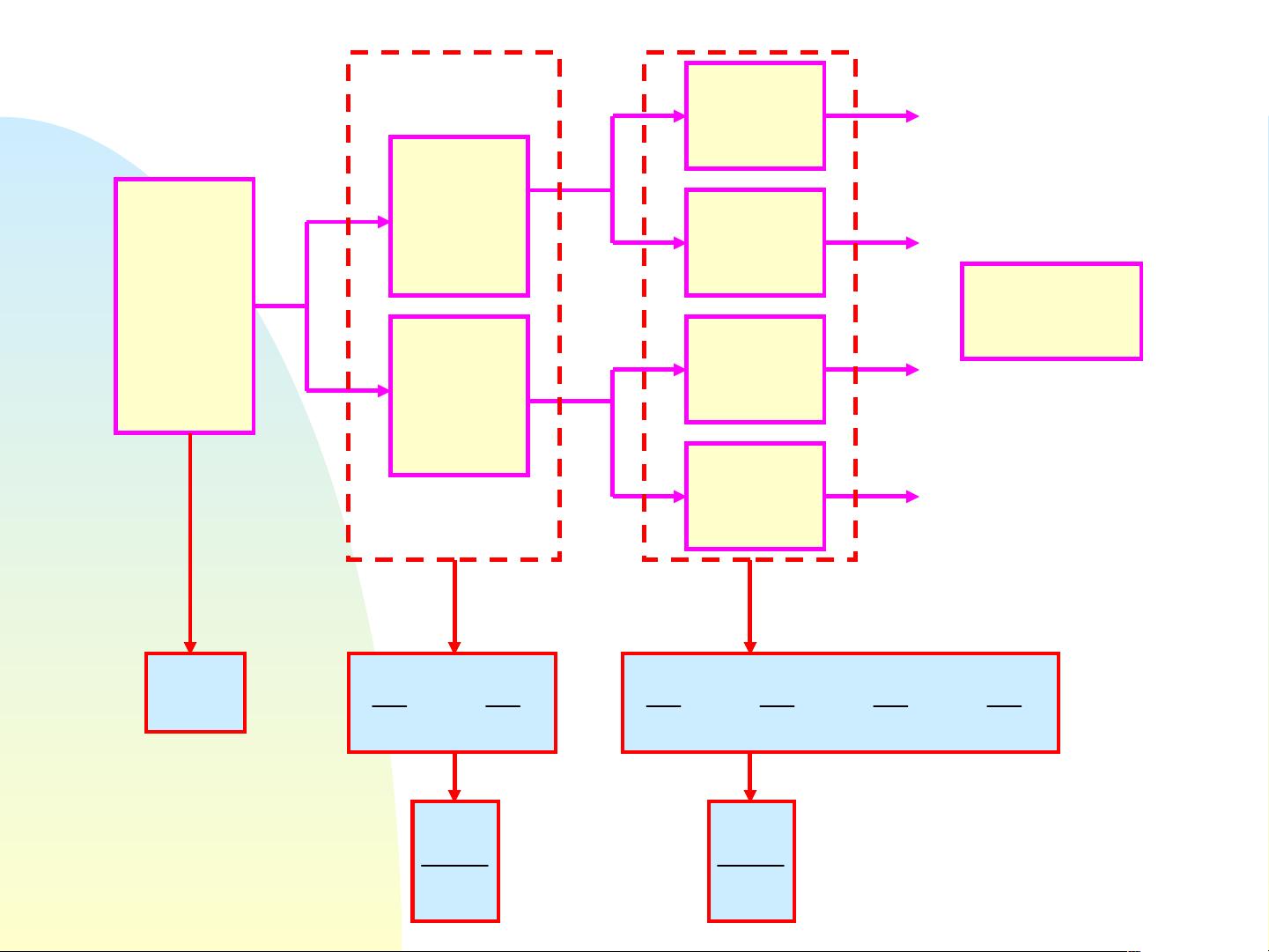 FFT算法的出现解决了这个问题。它将DFT分解为更小的子问题，然后利用对称性和分治策略减少计算量。基本的FFT算法包括Cooley-Tukey算法，它分为两大类：蝶形结构的时间抽取法和频率抽取法。这两种方法均基于分解DFT矩阵为对角线和反交换子矩阵的乘积，从而减少乘法数量。 时间抽取法（如radix-2 FFT）是针对序列长度为2的幂的情况，它通过交错和折叠操作将DFT分解为较小的DFT。而频率抽取法则是在计算完DFT后进行，通过选择特定频率的输出来重建整个DFT。虽然这两种方法在实现上有所不同，但它们都显著减少了计算量。 对于不满足2的幂的序列长度，可以使用混合基或组合数基四FFT等算法，这些算法结合了不同的分解策略来处理任意长度的DFT。 FFT的高效性使得它成为信号处理、图像分析、数字滤波、通信系统等多个领域的标准工具。通过优化的FFT实现，可以快速有效地处理大量数据，极大地提高了计算效率，使得实时分析和处理大型数据集成为可能。