EVIEWS软件时间序列分析实验教程

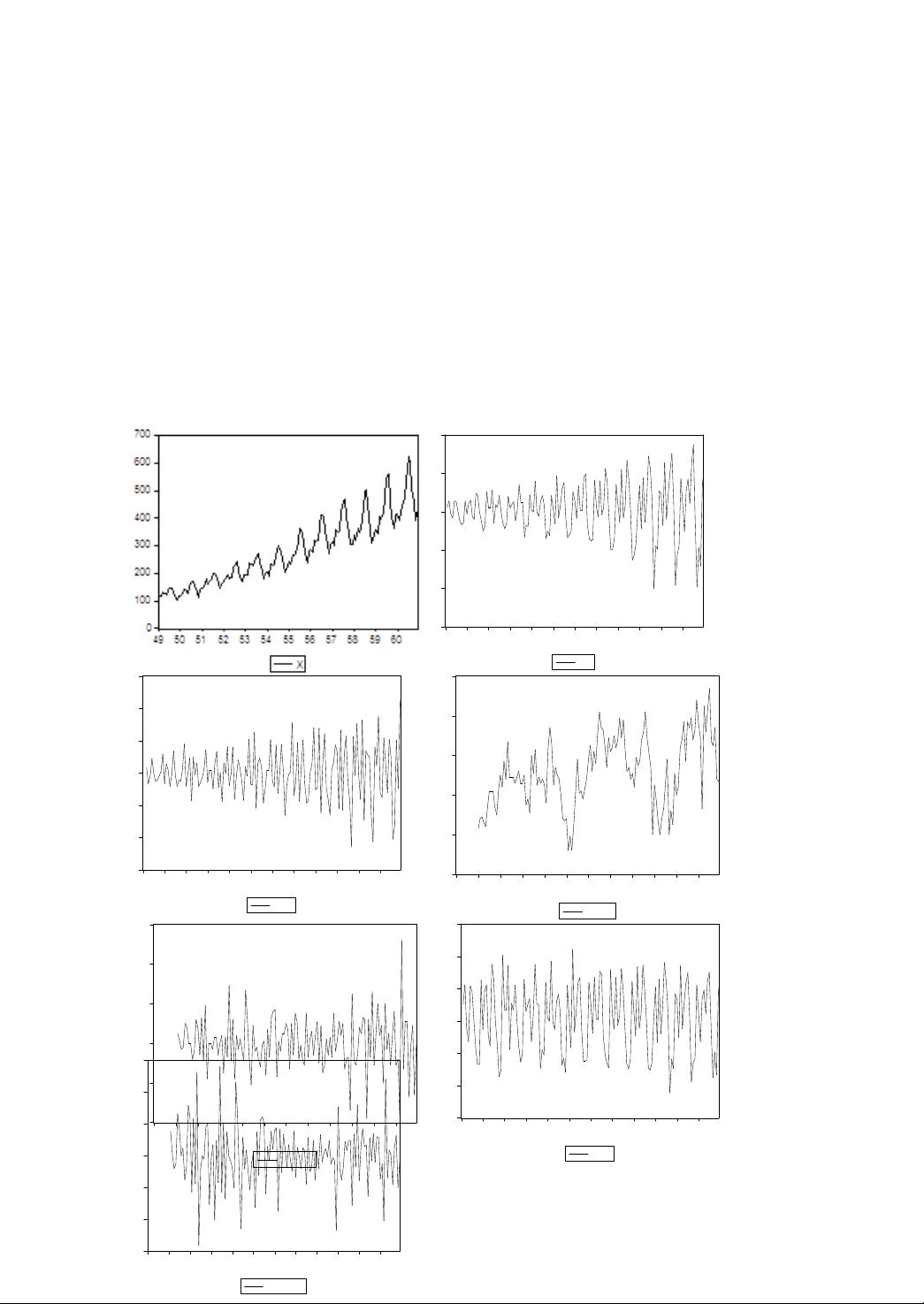
"时间序列分析实验指导" 时间序列分析是一种统计方法，用于研究和预测按时间顺序排列的数据序列。在本实验中，重点是利用EVIEWS软件对不同类型的平稳时间序列模型进行拟合分析。EVIEWS是一款强大的经济学和统计学应用软件，常用于数据分析、回归分析、时间序列建模等任务。 实验内容涵盖了多个关键环节： 1. **平稳时间序列模型**：平稳时间序列是指其统计特性（如均值、方差和协方差）不随时间变化的序列。这类模型对于预测和建模非常重要，因为它们假设未来数据的概率分布与过去相似。 2. **AR(p)模型**：自回归模型（AR模型）描述了当前观测值与过去若干期观测值的线性组合。AR(p)模型中，p表示过去观测值的数量。这个模型用于捕捉序列的自相关性。 3. **MA(q)模型**：移动平均模型（MA模型）则考虑了当前观测值与过去的误差项的线性组合。在MA(q)模型中，q是误差项的数量。这种模型用于处理残差序列的自相关性。 4. **ARMA(p,q)模型**：自回归移动平均模型（ARMA模型）结合了AR和MA模型的特点，它同时包含自回归项和移动平均项。ARMA(p,q)模型中的p是自回归项的阶数，q是移动平均项的阶数，用于捕捉更复杂的序列结构。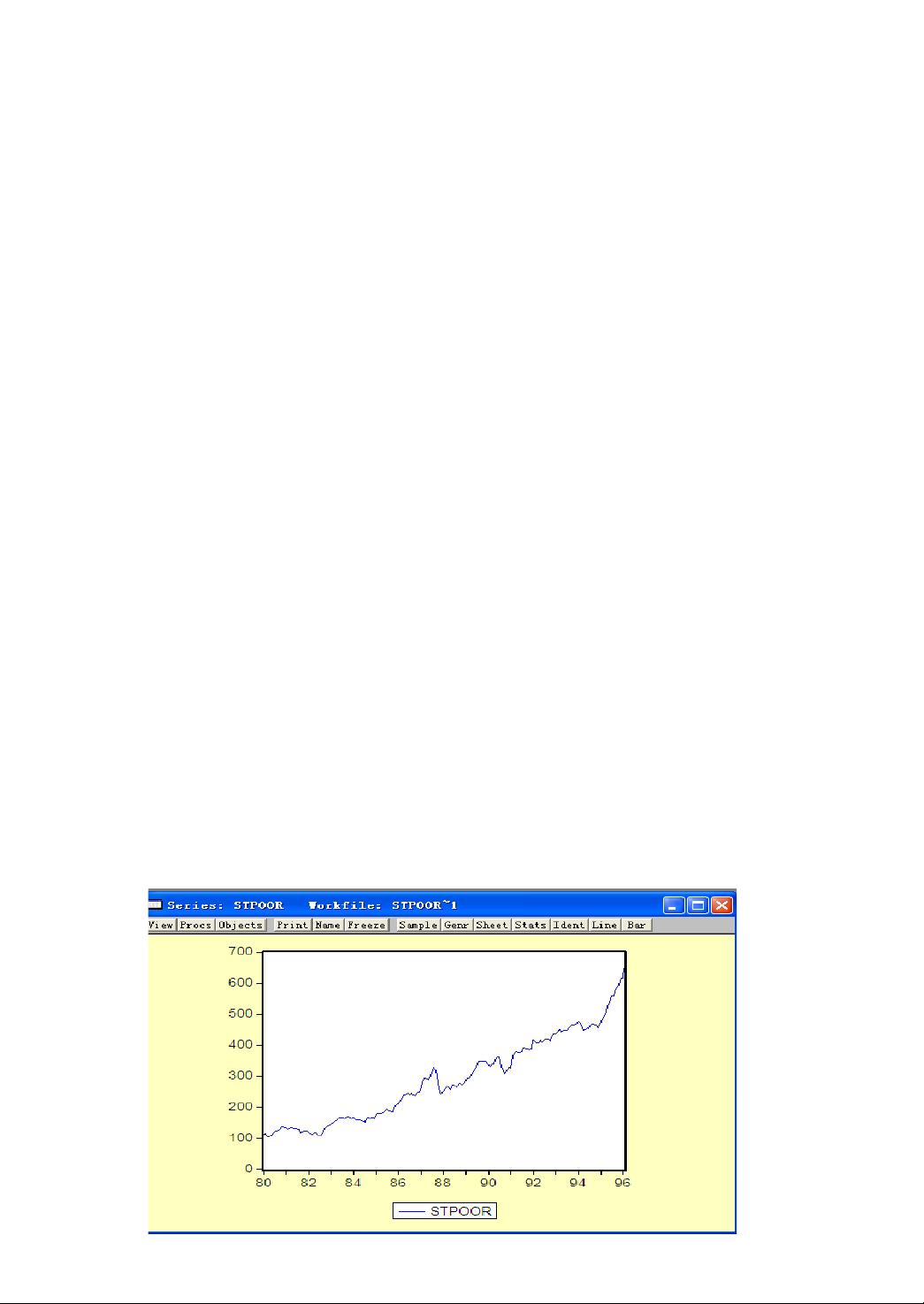 实验中，学生将通过以下步骤学习和应用这些模型： - **相关函数操作**：了解Eviews的菜单和命令方式，这包括创建工作文件、输入数据以及执行各种时间序列分析操作。 - **时间序列的差分**：差分是将序列转化为平稳的过程，包括简单差分和季节性差分，有助于消除趋势和季节性。 - **自相关和偏自相关图**：通过这些图形可以识别序列的自相关性和滞后效应，帮助确定AR和MA模型的阶数。 - **模型识别、检验和诊断**：建立ARMA模型后，需通过AIC、BIC准则选择最佳模型，并进行拉格朗日乘子检验（Lagrange Multiplier Test）和残差诊断，确保模型的有效性和无自相关性。 - **预测**：利用选定的ARMA模型进行未来数据的预测，这是时间序列分析的重要应用之一。 - **非平稳性检验**：如ADF（Augmented Dickey-Fuller）检验，判断序列是否为非平稳，以便采取适当的差分或转换。 这套实验教学指导书强调理论与实践的结合，通过实际案例和应用软件操作，提升学生的分析能力和模型建立技能。此外，还介绍了其他统计软件，如SPSS、SAS、MATLAB，旨在拓宽学生的视野，提高他们解决实际问题的能力。实验旨在逐步引导学生理解时间序列分析的全过程，从数据预处理到模型构建、检验和预测，从而更好地理解和应用时间序列分析方法。