tortion. Therefore most high
quality audio measurement
equipment includes a provi
-
sion for a dedicated analog
oscillator which is used for
THD+N testing.
Digital sinewaves may be
generated in several different
ways. The most common are
table look-up and polynomial
approximation. The table
look-up method is fast but
suffers from time resolution
limitations driven by the lim
-
ited length of the table. Com
-
mercial direct digital synthesis
chips are implemented this
way. Theoretical analyses (for
example Tierney et al, 1971)
have shown that the sine rom
length should be at least 4
times the data width output
from the rom. This makes the
distortion introduced by
quantization in the sample
timing equal to the distortion
introduced by quantization in
the data word. Both of these
errors may be converted to
white noise through proper
use of dither or error feedback
techniques. The polynomial
approximation technique yields sine
accuracies dependent on the number
of terms in the power series expansion
used. Arbitrarily accurate signals may
be obtained at the expense of compu
-
tation time.
Finger (1986) has shown that
proper signal generation in digital sys
-
tems requires that the generated fre
-
quencies be relatively prime to the
sample rate. If frequencies are used
which are submultiples of the sample
rate, the waveform will exercise only a
few codes of the digital word. For ex
-
ample, generating 1 kHz in a 48 kHz
sample rate system will require only 48
different data values. This may leave
large portions of a converter untested.
If frequencies are used which are
prime to the sample rate then eventu
-
ally every code in the data word will be
used. Using 997 Hz instead of 1 kHz
will result in all codes of a digital sys
-
tem (operating at standard sample
rates) being exercised. This frequency
makes a good “digital 1 kHz” since it is
also prime to the 44.1 kHz consumer
standard sampling frequency.
Dither is one of the most misunder-
stood aspects of digital signal genera
-
tion. When a signal is created in a finite
word length system, quantization
distortion will be introduced.
Vanderkooy and Lipshitz (1987) have
shown that the proper addition of
dither to the signal before truncation to
the final word width will randomize the
distortion into noise. This comes at a
3dB (overall) increase in the back
-
ground noise level. However, it allows
the generation of signals below the
system noise floor, and it frees large
amplitude signals of any distortion
products far below the system noise
floor. This is illustrated in Fig. 4 which
shows two FFTs of a 750 Hz tone over
-
laid on the same axes. The first is with
16 bit resolution, but no dither. The
second is with correct amplitude trian
-
gular dither. Dither randomizes the
distortion products into a smooth
noise floor below the peak level of the
distortion.
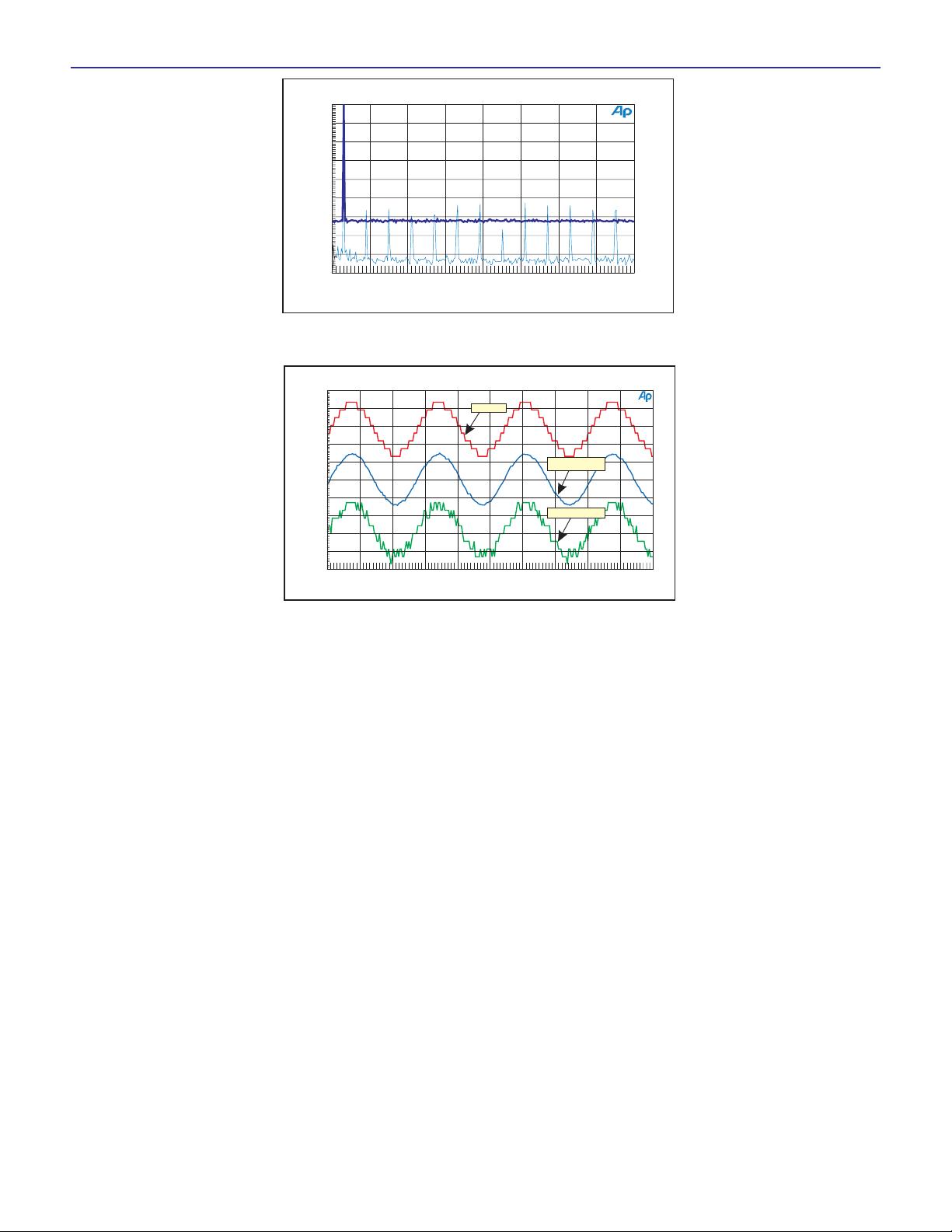
A smaller amplitude ver
-
sion of this same signal is
shown in the time domain in
Fig. 5. The upper trace shows
the sinewave with no dither.
The samples are limited to 16
bit resolution, which results
in the familiar digital stair
step waveshape. Note that
each cycle repeats the same
sample values. The lower
trace shows the same
sinewave with triangular
dither. The sample values are
different on each cycle,
though they still are re
-
stricted to the 16 bit system
resolution. The middle trace
shows the average of 64 of
the dithered sinewaves. The
same sample values now av
-
erage out to values between
that limited by the 16 bit sys
-
tem. Dither randomizes the
limited resolution of the 16
bit system into a smooth
waveform with resolution
much better than the sample
resolution permits.
Complex Signal
Generation
The multitone techniques discussed
later require a means of generating mul-
tiple sinewaves simultaneously. For
small numbers of sines this may be done
with real-time computation of each sine
in a dsp and subsequent summation.
For larger numbers of tones rom or ram
based waveform generation is normally
used. For analog applications this is
passed through a D/A converter. The
rom size sets the waveform length be
-
fore repeating, and therefore sets the
minimum spacing of tones. The typical
size in commercial equipment is 8192 or
16384 points which gives an approxi
-
mately 6 or 3Hz spacing respectively at
a 48 kHz sample rate.
Other waveforms such as those
used for monotonicity testing of A/D
converters may be created using table
look-up techniques, or they may be
computed in real time. For signals
which do not need control of their pa
-
rameters such as repetition rate or fre
-
quency, the look-up table approach
has a speed advantage. It does how
-
Fundamentals of Modern Audio Measurement
-180
+0
-160
-140
-120
-100
-80
-60
-40
-20
d
B
F
S
0
20k
2.5k 5k 7.5k 10k 12.5k 15k 17.5k
Hz
Fig. 4. Illustration of distortion reduction in return for higher noise
floor with the addition of dither.
Audio Precision 04/17/97 14:16:46
-0.05
0.05
-0.04
-0.03
-0.02
-0.01
0
0.01
0.02
0.03
0.04
%
F
S
0 5m500u 1m 1.5m 2m 2.5m 3m
sec
UNDITHERED
TRIANGULAR DITHER,
64 AVERAGES
3.5m 4m 4.5m
TRIANGULAR DITHER
Fig. 5. Effectiveness of dither illustrated with 16 bit quantized signal.









