优化医院选址：最小化城市中最远路程

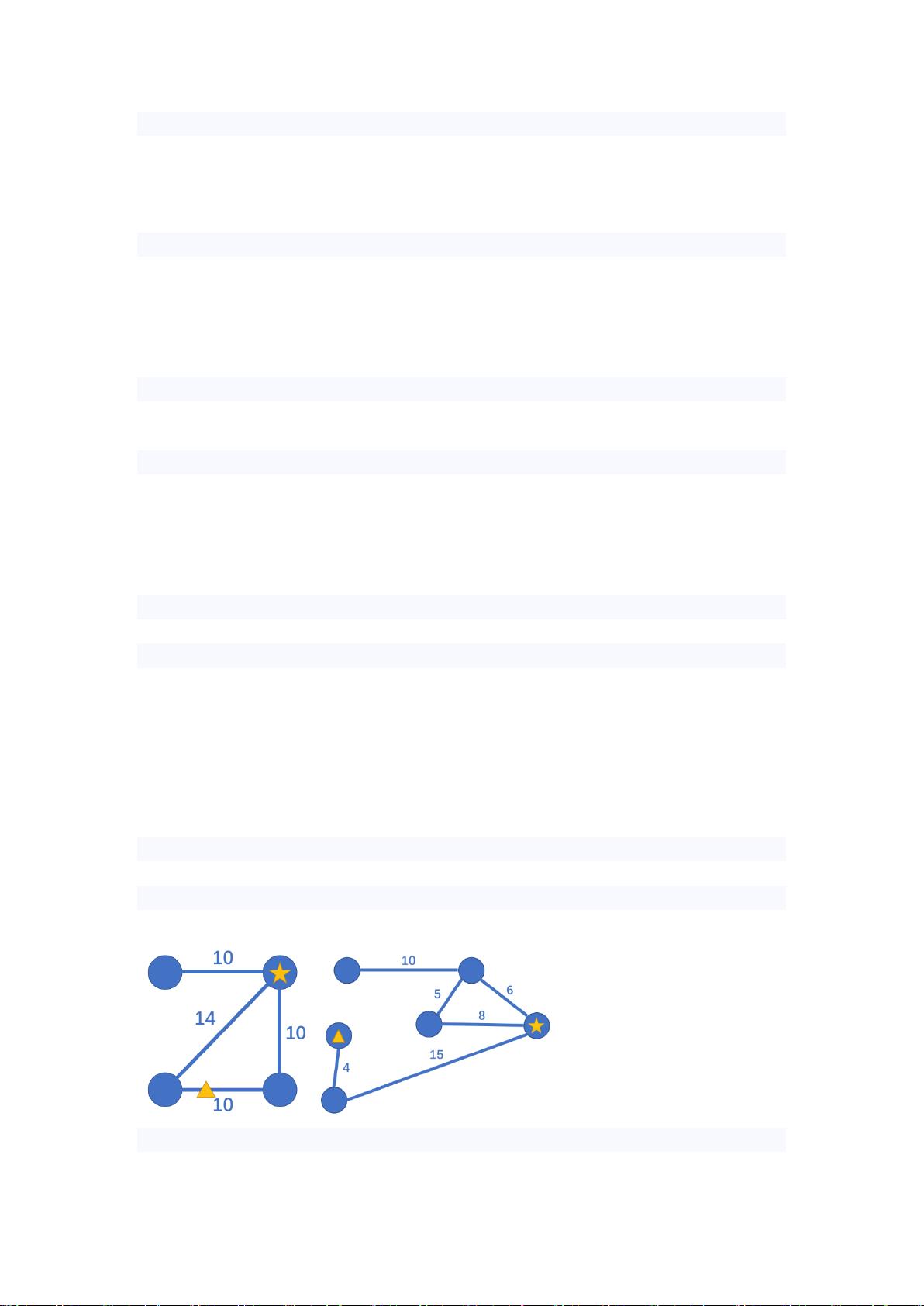
"实验题目1" 本实验涉及的是图论中的经典问题，目标是在给定的城市道路网络中找到一个位置建立医院，使得所有居民到医院的最长时间尽可能短。这个问题可以被解释为寻找图的中心点或者最小生成树的中心节点，以确保覆盖范围最广。 首先，我们需要理解输入格式。输入包含两个整数N和M，分别代表城市中的交叉路口数量（节点数）和道路数量（边数）。接下来的M行描述了每条道路，每行包含三个正整数x、y和t，表示从节点x到节点y有一条需要时间t的道路。保证图是连通的，没有重复的边或自环。 对于输出，我们需要计算出在最佳医院位置选定后，城市中任意一点到医院的最长时间，并保留两位小数。 样例输入一和样例输入二展示了不同规模的问题实例，给出了相应的最优解。例如，样例输入一中，当医院建在特定位置时，最远的居民到医院的时间是17.00分钟；而在样例输入二中，这个时间是19.00分钟。 解决这类问题的方法可以是使用最短路径算法，如Dijkstra算法或Floyd-Warshall算法，找出所有点到其他点的最短路径，然后分析这些路径以确定最小最大时间。另一个可能的策略是使用Prim或Kruskal算法构建最小生成树，然后找出树的中心节点。 在实际编程实现中，由于C#语言标签的提示，我们可以使用C#的图数据结构库，如`System.Collections.Generic`中的`Dictionary`或`LinkedList`来表示图，用`Queue`或`PriorityQueue`来辅助实现最短路径算法。同时，需要注意优化算法效率，例如，使用优先队列（堆）可以提高Dijkstra算法的性能。 在解决这类问题时，还需要考虑数据规模，如本题中N≤100，M≤500或M≤150，以及边权的范围0<边权≤100，确保算法能在合理的时间内完成计算。在实际应用中，可能需要进行复杂度分析并考虑更高效的算法，例如使用启发式方法或近似算法来处理大规模数据。