维纳滤波器详解：最小均方误差估计应用

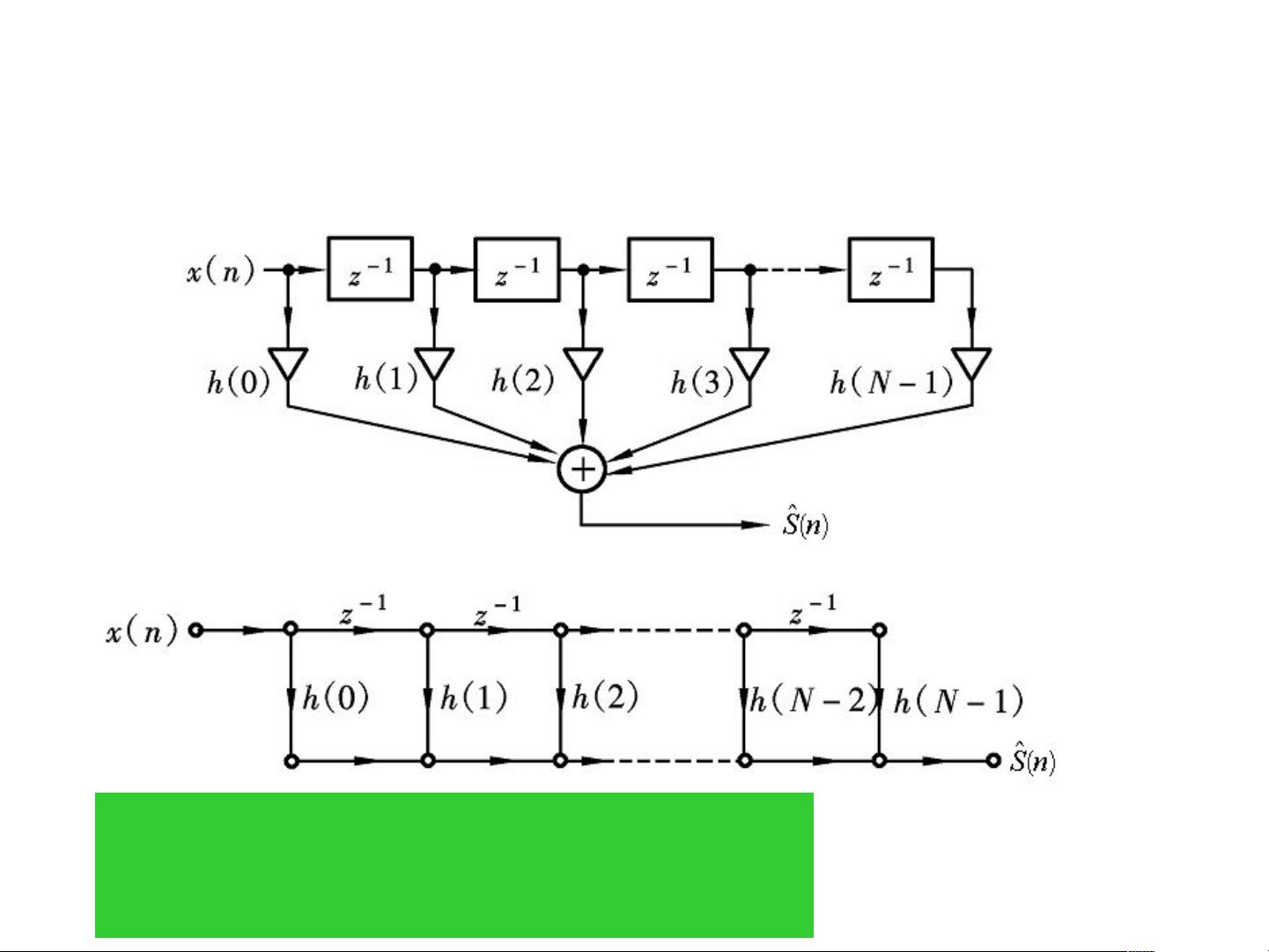
"本文主要介绍了维纳滤波器的基本概念、类型及其在数字信号处理中的应用，特别是作为最小均方误差估计的一种方法。内容涵盖了维纳FIR滤波器、非因果IIR滤波器、因果IIR滤波器以及维纳预测器的设计和计算示例。" 维纳滤波器是一种在信号处理领域广泛应用的滤波技术，它主要用于通过最小化均方误差来估计真实信号。在信号处理中，我们常常面临的问题是，由于各种噪声或干扰，我们只能观测到被污染的信号，而无法直接获取原始信号。维纳滤波就是解决这一问题的有效工具，它提供了一个线性滤波器，可以对测量数据进行平滑处理，以尽可能接近真实信号。 1.1 维纳滤波问题描述：维纳滤波的核心是寻找一个滤波器，该滤波器能将观测数据转换成对真实信号的最小均方误差估计。这种滤波问题可以应用于信号平滑、滤波和预测等多个场景。 1.2 维纳FIR滤波器：有限 impulse response (FIR) 滤波器是一种线性时不变系统，其输出是输入信号的历史样本与一组固定系数的线性组合。在维纳滤波器的上下文中，FIR滤波器的设计目标是找到最佳的系数集，以最小化误差平方和。 1.3 维纳非因果IIR滤波器：无限 impulse response (IIR) 滤波器允许反馈，因此可以使用较少的系数实现更宽的频率响应。非因果IIR滤波器则假设未来的信息可用于当前的估计，这在实际应用中通常是不可能的，但理论分析有价值。 1.4 维纳因果IIR滤波器：在实际应用中，我们通常需要的是因果滤波器，即只有过去的和当前的输入信号才能影响当前的输出。维纳因果IIR滤波器满足这一条件，同样寻求最小化均方误差。 1.5 预备知识：理解和设计维纳滤波器需要掌握线性代数、随机过程和优化理论等基础知识。 1.6 维纳IIR滤波器计算例子：通过线性代数的方法，可以求解滤波器的单位脉冲响应（h(n)），从而实现滤波器的设计。这通常涉及到解正交方程来确定滤波器参数。 1.7 维纳预测器：预测器是一种特殊的滤波器，用于预测未来的信号值，基于过去和当前的观测数据。在维纳滤波框架下，预测器也遵循最小均方误差原则。 维纳滤波器是一种强大的数学工具，它在信号处理和控制理论中有着广泛的应用，如图像处理、通信、声音恢复等领域。通过理解和应用维纳滤波器，工程师们能够设计出高效的滤波算法，以提高信号质量并减小噪声的影响。