MATLAB实现蒙特卡洛方法详解：概率与随机变量应用

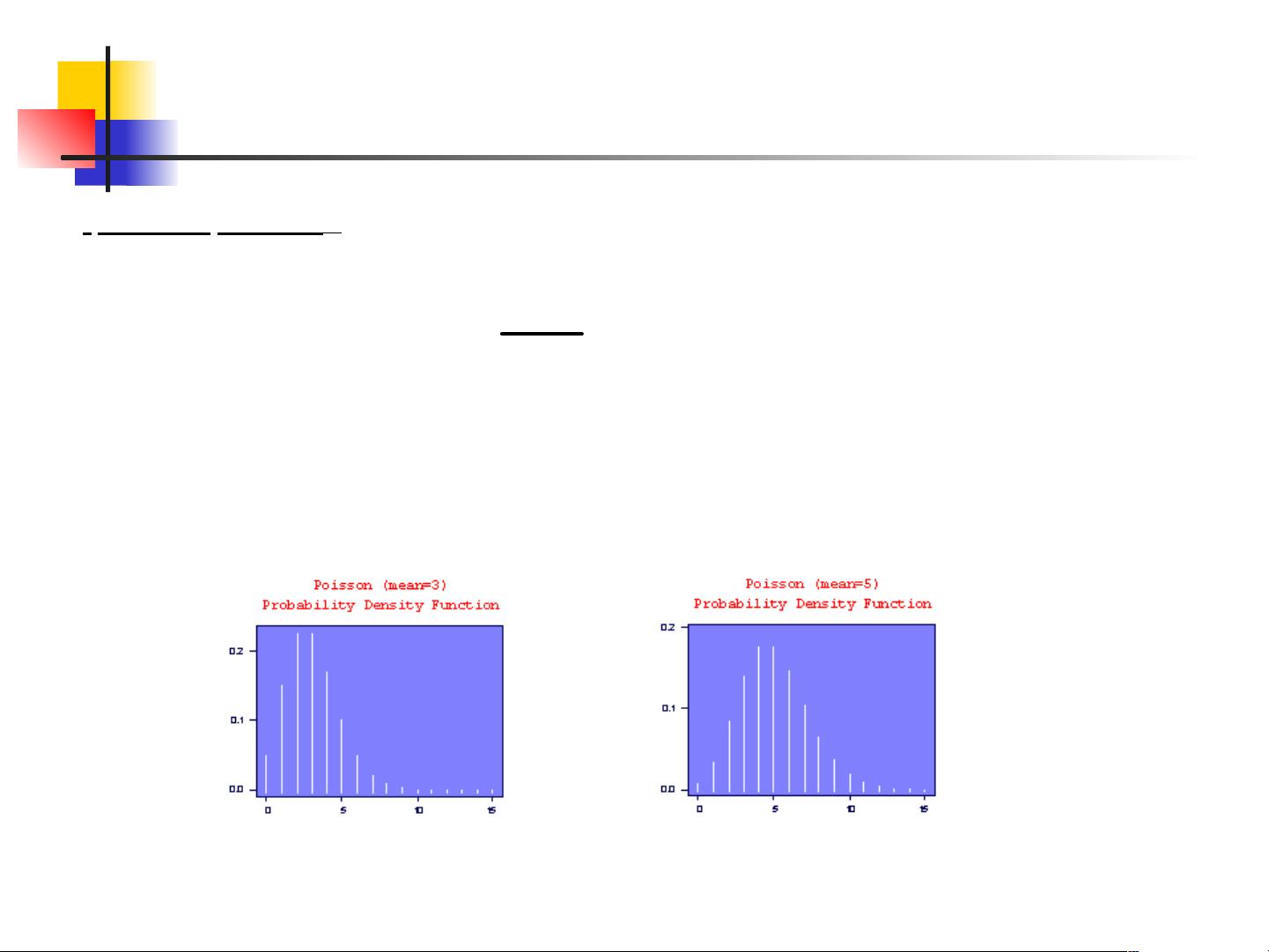
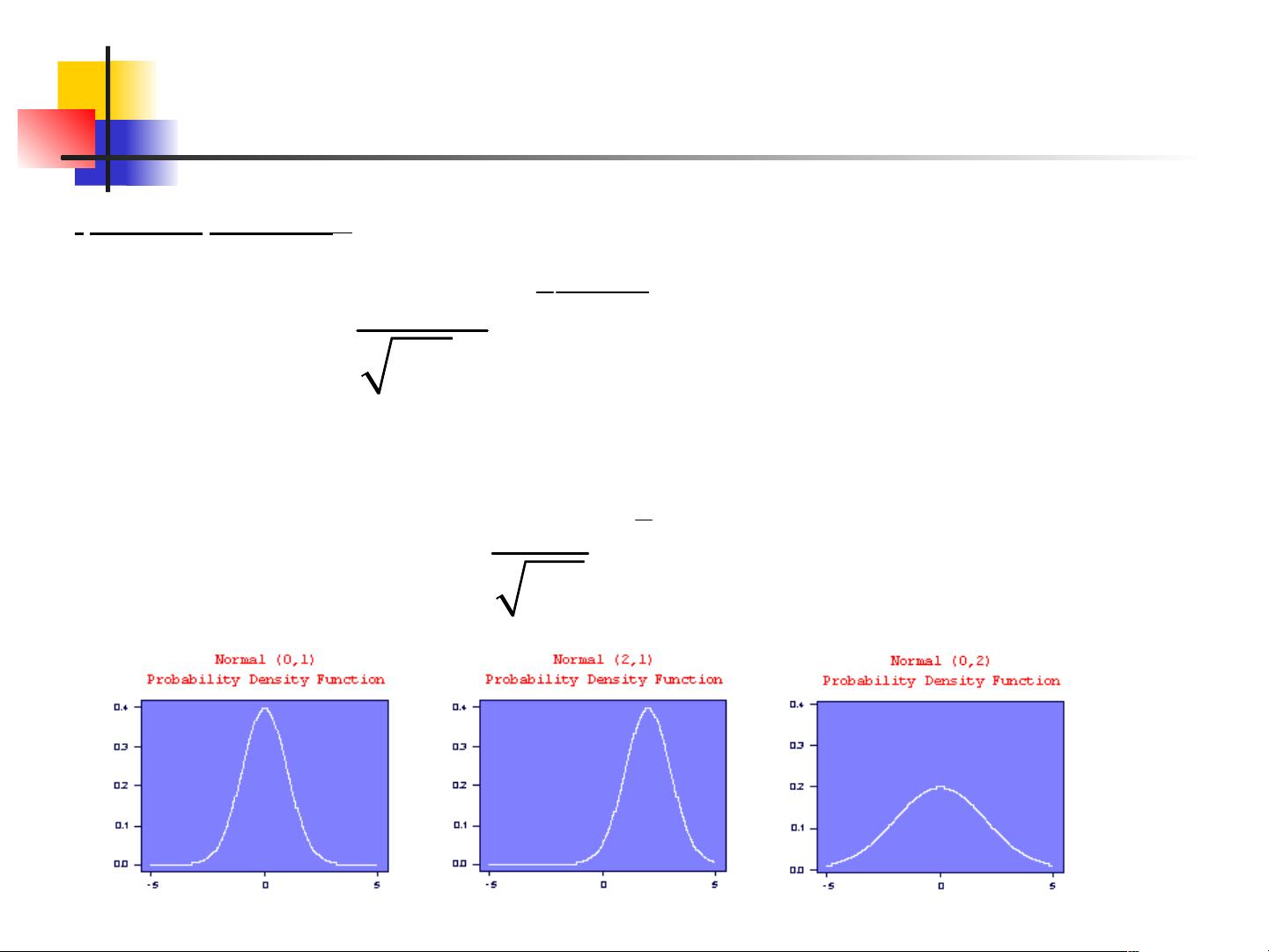
本资源是一份关于MATLAB中的蒙特卡罗方法的学习资料，它通过PowerPoint形式呈现，详细介绍了蒙特卡罗方法的基本概念和应用。主要内容包括以下几个部分： 1. 第二章 - 蒙特卡洛方法 - 概率与统计基础：这部分讲解了基本的概率论概念，如概率的加法原理（A OR B）、乘法规则（A AND B），以及条件概率和互斥事件、相互独立事件的概念。通过古典概率的介绍，阐述了随机事件在相同实验条件下发生的概率。 2. 全概率公式和贝叶斯公式： - 提供了如何通过全概率公式计算事件B在事件A已知情况下的概率，以及贝叶斯公式，用于更新先验概率为后验概率，适用于随机事件集合的情况。 3. 随机变量： - 区分离散随机变量和连续随机变量，前者如光电效应、Compton散射等反应过程的反应几率，后者则涉及分布函数和概率密度函数的计算。 - 分布函数和联合分布密度的概念，以及随机变量之间相互独立时的密度函数关系。 4. 函数的分布密度和随机变量的特征值： - 讲解如何通过随机变量的密度函数计算函数值的期望和方差，以及变量变换（例如Jaccobi变换）对概率分布的影响。 5. MATLAB的应用： - 提供了利用MATLAB实现蒙特卡罗模拟的方法，这些方法通常用于解决复杂问题，如数值积分、随机模拟和估计，因为它们能够处理难以解析求解的问题，依赖大量随机样本来逼近真实结果。 这份资料不仅适合初学者了解蒙特卡罗方法的理论，也对MATLAB用户在实际项目中应用蒙特卡罗技术具有指导意义。通过学习，读者可以掌握如何运用MATLAB进行概率分析和模拟，提升对随机现象的理解和处理能力。