MATLAB一维插值详解

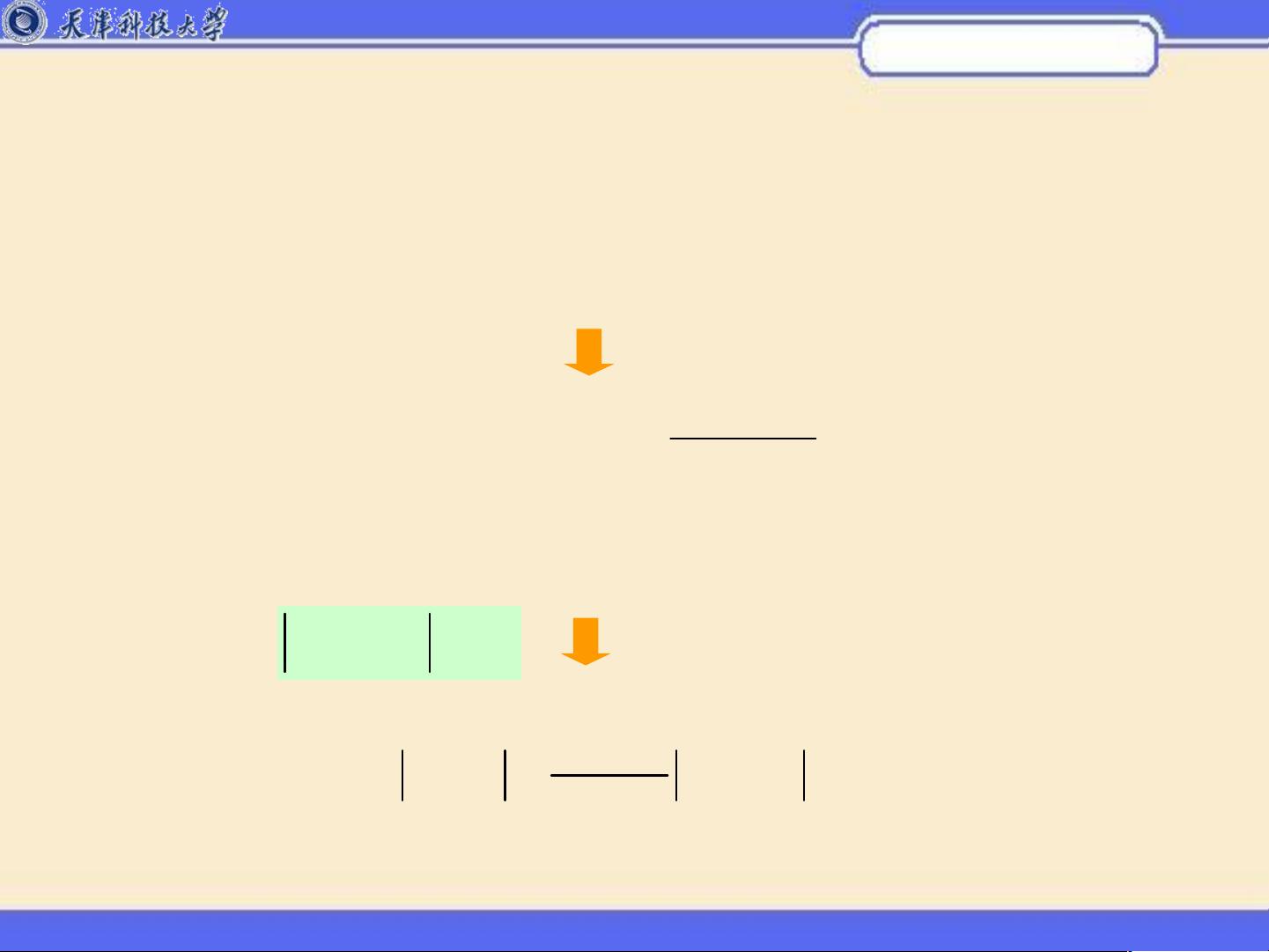
"MATLAB插值PPT学习资料，讲解了从一维到高维的插值方法，适合学习和参考。" MATLAB插值是一种在给定数据点之间构建连续函数的技术，常用于数据拟合、数据分析和科学计算中。在MATLAB中，插值可以帮助用户估计未知数据点的值，尤其是在数据点稀疏或不连续的情况下。本资源主要涵盖了三个维度的插值方法：一维插值、二维插值和高维插值。 一、一维插值 一维插值问题通常涉及到寻找一个简单且易于计算的函数，该函数通过已知的n+1个数据点（节点），使得在这些点上的函数值与实际数据相匹配。一维插值的基本思想是构建一个次数不超过n的代数多项式来逼近原函数。例如，如果n=1，我们可以使用线性插值；如果n=2，我们可以使用二次插值。 1. 数学描述：假设我们有一系列数据点 (x0, y0), (x1, y1), ..., (xn, yn)，目标是找到一个n次多项式f(x) = a0 + a1x + ... + anxn，满足f(xi) = yi，对于所有的i从0到n。 2. 多项式插值：利用拉格朗日插值公式或者牛顿插值公式，可以构建出一个满足所有节点值的插值多项式。然而，当n较大时，由于插值多项式的计算量增加，这种方法可能会变得复杂且效率低下。 二、二维插值 二维插值扩展了一维插值的概念，适用于处理平面内的离散数据集。在MATLAB中，可以使用如`griddata`函数来实现二维插值，它允许用户在不规则的数据网格上进行插值。例如，如果你有一个网格状的数据点，你可以找出任意坐标点的函数值。 三、高维插值 在多于两个自变量的情况下，高维插值更加复杂，但MATLAB提供了如`interpn`函数来处理这类问题。高维插值通常用于处理复杂的多变量数据，如图像处理和多参数数据分析。 在学习MATLAB插值时，理解插值的基本原理、选择合适的插值方法以及熟悉相关的MATLAB函数是关键。此外，掌握如何评估插值的精度以及避免过插（即插值函数过于复杂导致过度拟合）也是重要的实践技巧。 MATLAB插值的应用广泛，包括但不限于工程计算、物理模拟、图像处理、信号处理等领域。通过PPT学习资料，可以深入理解插值的各种方法，并通过实际案例提高应用能力。建议结合提供的链接资源，如MATLAB天空论坛和ILoveMATLAB论坛，进行更深入的学习和交流。