数学建模常用算法解析：神经网络、遗传算法与模拟退火

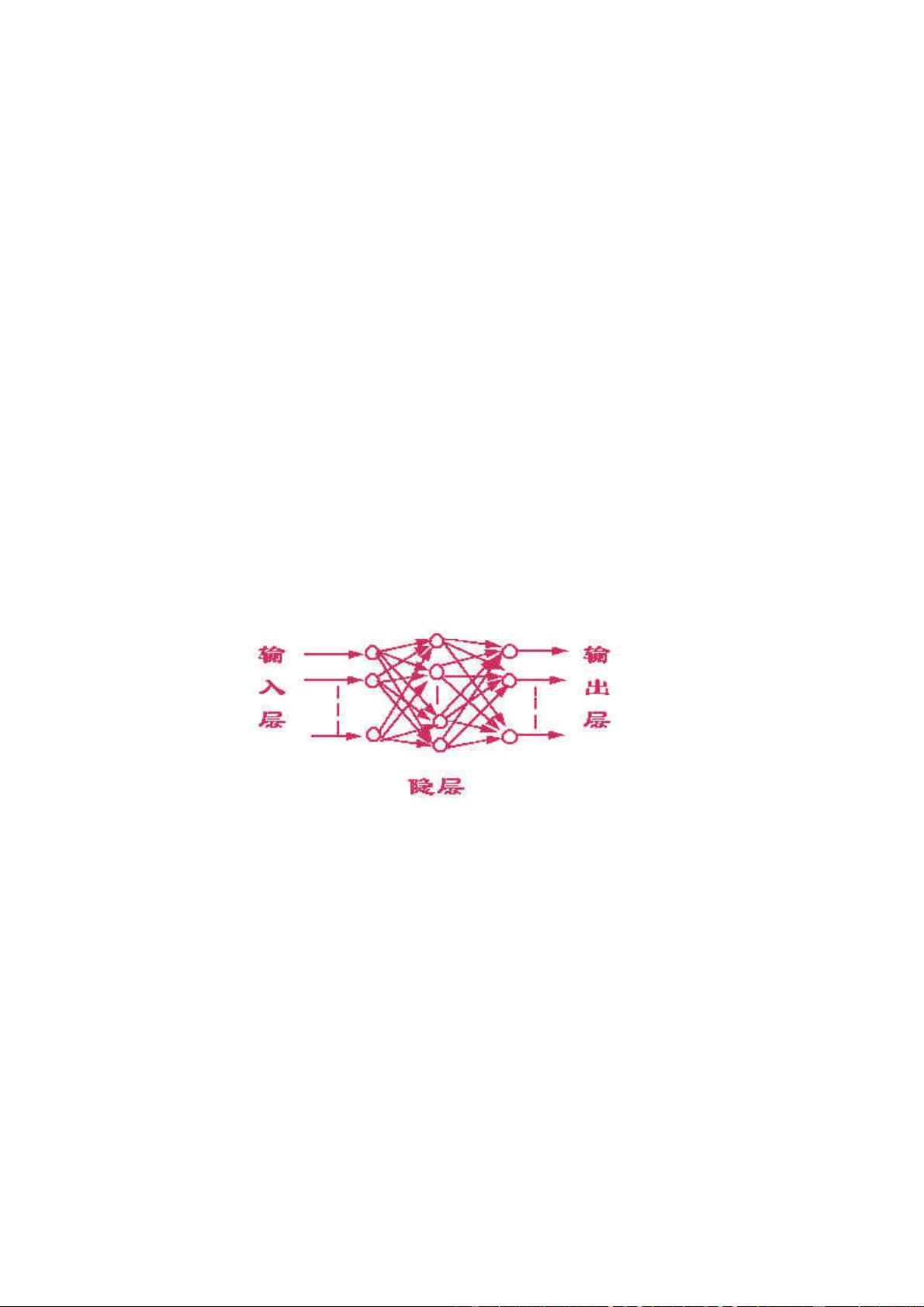
本讲义主要探讨了在处理复杂事务时可以采用的几种经典算法，包括神经网络算法、遗传算法、模拟退火算法和模糊数学方法。这些算法在解决复杂问题，尤其是那些传统方法难以解决的问题时表现出高效性。讲义的重点是应用而非深入理论，旨在帮助读者理解算法的基本原理，识别它们能解决的问题类型，并提供了可以直接使用的程序代码。 1. **神经网络算法**： - **基本原理**：神经网络模仿人脑认知过程，通过训练（调整权重）以适应输入输出关系，使得给定输入时能够预测输出。 - **结构**：神经网络通常包含输入层、输出层和隐藏层，层数决定精度与计算时间，需根据实际需求设计。 - **神经元**：每个节点代表一个人工神经元，有多个输入和一个输出，激活函数影响网络性质和用途。 - **分类**：讲义提到了感知器和反向传播（BP）网络。 - **感知器**：最简单的神经网络，使用阶跃函数，主要用于分类问题。 - **BP网络**：最常用且重要的神经网络，多层结构，通常使用S型激活函数（如正切或对数函数），能用于函数逼近、模式识别和分类等任务。 2. **其他算法**： - **遗传算法**：基于生物进化原理的搜索算法，通过模拟自然选择和遗传操作来优化问题解决方案。 - **模拟退火算法**：灵感来自固体冷却过程，用于全局优化，避免在局部最优解中停滞。 - **模糊数学方法**：处理不精确或不确定信息的工具，适用于处理模糊逻辑和不确定性问题。 在面对复杂事务时，选择合适的算法至关重要。例如，如果问题是分类问题，可以考虑使用感知器；如果是需要逼近复杂函数或进行非线性问题解决，BP网络可能更为适用。同时，遗传算法和模拟退火算法在处理全局优化问题时表现出色。理解这些算法的工作原理和应用场景，能帮助开发者更有效地解决实际问题。提供的程序代码则可以直接应用于实践中，简化问题求解的过程。