November 10, 2008 / Vol. 6, No. 11 / CHINESE OPTICS LETTERS 871
Size measurement of nano-particles using self-mixing effect
Huarui Wang (
uuu
HHH
)
1,2
and Jianqi Shen (
!!!
ïïï
jjj
)
1
1
University of Shanghai for Science and Technology, Shanghai 200093
2
Xuzhou Normal University, Xuzhou 221116
Received February 27, 2008
In this letter, the technique of laser self-mixing effect is employed for nano-particle size analysis. In
contrast to the photon correlation spectroscopy (PCS) and photon cross correlation spectroscopy (PCCS),
the main advantages of this technique are sensitive, compact, low-cost, and simple exp erimental setup etc.
An improved Kaczmarz p rojection method is developed in the inversion problem to extract the particle
size d istribution. The experimental results prove that nano-particle size can be measured reasonably by
using the self-mixing effect technique combined with the improved projection algorithm.
OCIS codes: 290.5820, 290.5850, 290.1350, 290.3700.
doi: 10.3788/COL20080611.0871.
The characteristics of many modern materials are often
determined by the properties of nano-particle, especially
the size of the particle. This fact is responsible for the
fast-growing demand for analysis on the nano-particle
size. Different kinds of techniques for nano-particle anal-
ysis app e ar in succession. Among them, the well-known
techniques are photon co rrelation spectro scopy (PCS)
and photon cross correlation spectroscopy (PCCS)
[1]
.
However, in the PCS and PCCS measurements, the
alignment is necessary where the laser and the detector
are placed at differ e nt locations, which suffers from the
complexity of preparation work before measurement. In
addition, in the P CS and PCCS principles, the c orrela-
tion function of the signal is analyzed by the expensive
correla tor, which leads to a rather high production cost.
Recently, the self-mixing effect technique is introduced
into the nano-particle size analysis
[2,3]
. The self-mixing
effect is an optical phenomeno n observed when light
emitted from a laser cavity reflects off an object and
re-enters the laser cavity after an external r ound trip
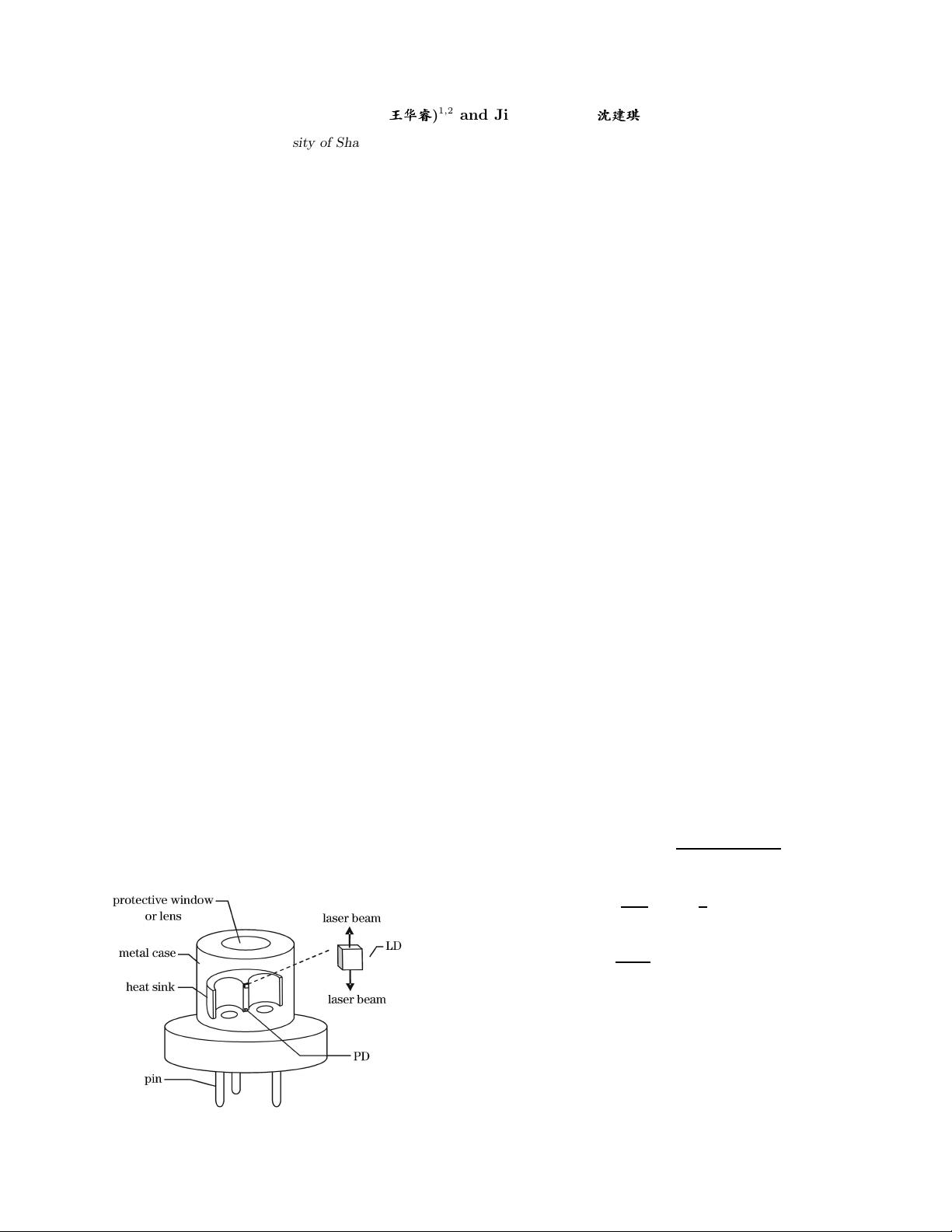
time. According to the apparatus shown in Fig. 1 in
which the laser diode and photodiode are integrated, the
self-mixing effect technique is very convenient to align.
Besides, it can avoid using the expensive corre lator. The
power spectrum is got through fast-Fourier transform
(FFT) instead and is analyzed for the restor ation of parti-
cle size. Therefore, the main advantag e of this technique
Fig. 1. Laser configuration.
is that it offers a sensitive, compact, low-cost, and sim-
ple experimental setup and hence it is very hopeful for
online applications. However, similar to the PCS and
PCCS techniques, the inverse problem in this technique
is ill-posed. Small errors in the measurement may give
rise to large spurious oscillations in the solution. In this
letter, the nano-particle size measurement bas e d on the
self-mixing effect is studied with a combination o f an im-
proved projection method in the data processing.
The principle of particle size measurement using self-
mixing effect is that the light e mitting fr om the laser
hits nano -particles with the Brownian motion and is scat-
tered back into the laser cavity. This causes the periodic
change of las e r light output frequency, linewidth, thresh-
old gain, and output power, all of which relate to the
phase of the backscattering light. The standard internal
monitoring photodiode, which is built into the co mmer-
cial las e r diode (LD) package, can be utilized to detect
the output sig nal and to observe the output linewidth.
The linewidth of the output power spectrum is related
closely to the particle size. Due to their higher average
velocity, small particles cause a greater sp e ctrum broad-
ening than la rge particles do. The intensity spectrum of
self-mixing effect follows from the Lorentz function
[2−4]
:
I(ω) = 2α
2
π
−1
n
p
κ
2
D (x)
ω
2
+ [κ
2
D (x)]
2
, (1)
κ (θ) =
4πn
λ
sin
θ
2
, (2)
D (x) =
k
B
T
3πηx
, (3)
where α is the polarizability of particle, n
p
is the average
number of particles in scattering volume, ω is the angu-
lar frequency, κ is the magnitude of the scattered wave
vector, n is the refractive index of the liquid medium,
D (x) is the self-diffusion coefficient, θ is the scattering
angle (θ = π in the self-mixing effect technique), k
B
T is
the B oltzmann factor, x is the particle diameter, and η
is the viscosity of the solvent.
Despite the advantages of self-mixing effect technique,
1671-7694/2008/110871-04
c
2008 Chinese Optics Letters









