八皇后与八数码问题：局部搜索算法详解

局部搜索算法是一种在搜索过程中只关注当前解状态而不关心具体搜索路径的方法，适用于许多领域，如八数码和八皇后问题，以及作业空间调度、自动程序设计等。在这些问题中，目标是找到满足条件的最佳解，而非搜索路径本身。 首先，我们来看几种常用的局部搜索算法： 1. 爬山法（hill climbing）：这是最基本的形式，每次迭代时选择具有最好评价函数值（如错误放置的棋子数量）的相邻解。然而，爬山法存在局限性，如可能导致局部最优而非全局最优，陷入高地或山脊，导致搜索效率下降。例如，在八数码问题中，爬山法可能会在某个状态停滞不前，因为找不到更好的邻接状态。 2. 随机重启爬山法：为了解决爬山法的局部最优问题，可以定期随机重置搜索过程，从不同的起点开始，增加找到全局最优解的概率。 3. 模拟退火算法：模拟金属冷却过程，允许搜索在低于当前最优解的温度下接受较差解，通过一定的概率机制跳出局部最优，增加了全局优化的可能性。 4. 遗传算法：模仿自然选择和遗传机制，通过生成并组合多个解（个体），通过适应度函数评估其优劣，从而逐步改进解决方案。遗传算法通常用于解决复杂问题，如八皇后问题，通过交叉和变异操作来生成新的解。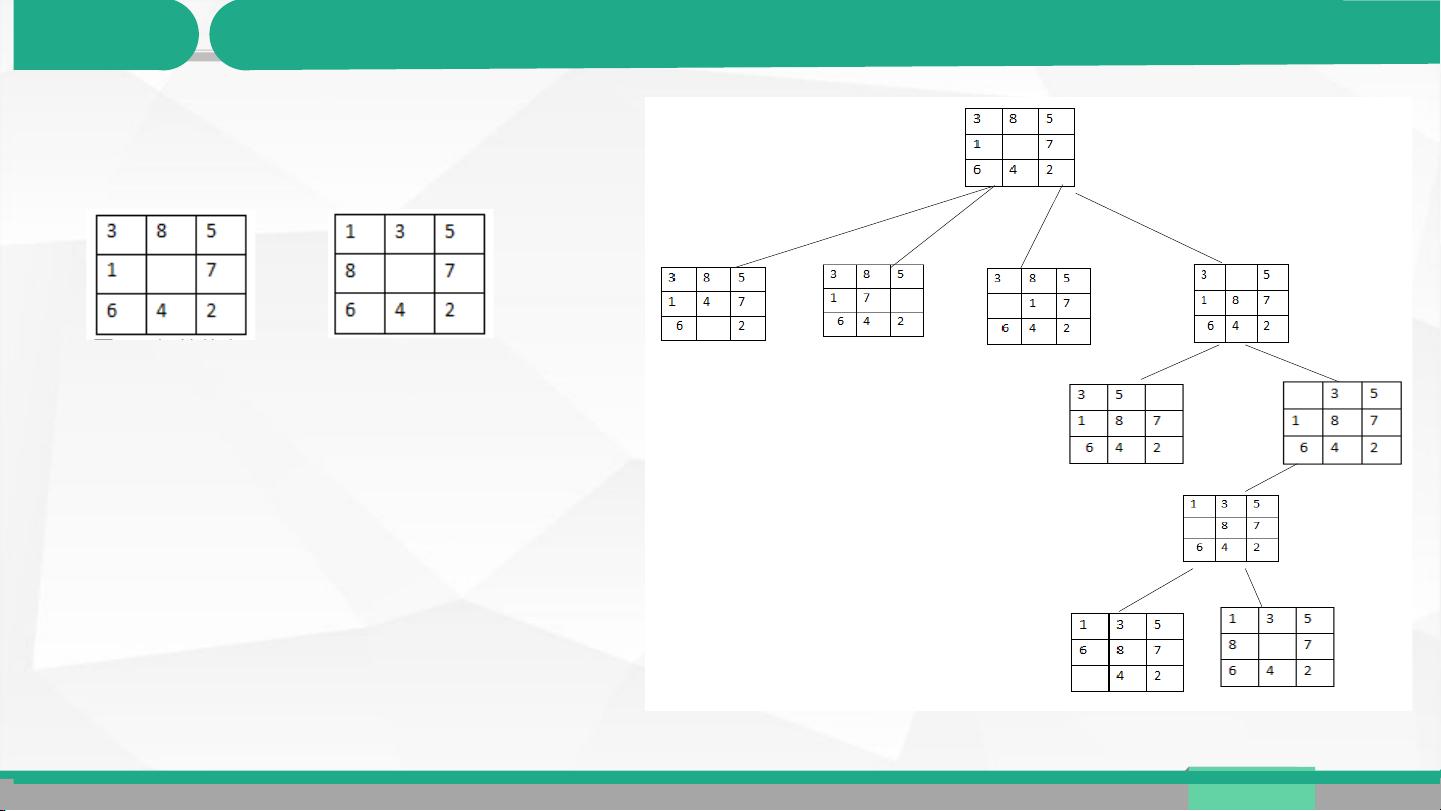 以八数码和八皇后问题为例，爬山法的具体步骤如下： - 对于八数码问题，从初始状态开始，计算每个邻接状态的评价函数值（错误棋子数）。 - 如果新状态的评价值更低，替换当前状态；如果相同或更高，则根据一定的策略（如随机或根据启发式函数）决定是否进行尝试。 - 重复这个过程，直到找到满足条件（错误棋子数为零）的目标状态。 对于八皇后问题，爬山法可能需要多次尝试，因为存在多种可能的解决方案，且可能陷入局部最优。而模拟退火算法和遗传算法则更注重通过全局视角寻找潜在的解决方案，能够避免局部最优陷阱。 局部搜索算法是解决复杂优化问题的重要工具，通过不同的策略和机制，能够在一定程度上提高搜索效率和找到全局最优解的可能性。然而，它们并非所有情况下都能保证最优，尤其是在面对具有复杂搜索空间的问题时，可能需要结合其他搜索技术或启发式方法。