MATLAB实现数字信号处理：案例分析与应用

本文主要探讨了数字信号处理中的几个关键概念和案例，涉及脉冲响应、滤波器设计以及在实际应用中如何处理受到高斯噪声干扰的信号。通过使用MATLAB工具进行可视化分析，深入理解这些核心概念。 在数字信号处理中，脉冲响应是一个重要的参数，它描述了一个系统对输入信号的响应。在案例2.27中，通过`impz`函数展示了系统的单位脉冲响应`hn`，这是当输入为单位阶跃函数时，系统输出的序列。图示显示了不同时间点`n`的响应值，帮助我们理解系统的动态特性。而`step`函数则用于展示系统在连续时间下的脉冲响应`yn`，这对于理解和设计数字滤波器至关重要。 案例2.29展示了卷积运算在信号处理中的应用，通过`conv`函数计算两个序列的卷积结果`y`。这在模拟信号通过线性系统时尤其有用，可以预测输出信号的形状。在这个例子中，`x`和`h`是输入和系统响应，它们的卷积表示了新系统的脉冲响应`yn3`。 高斯噪声是现实世界信号处理中常见的干扰源。案例2.30通过MATLAB生成了受到高斯噪声干扰的正弦信号`xn`。`randn`函数生成了均值为零、方差为1的标准正态分布随机数，这些随机数与正弦信号相加，模拟了高斯噪声的干扰。通过`stem`函数绘制出的信号波形，可以直观地看到噪声如何影响原始信号。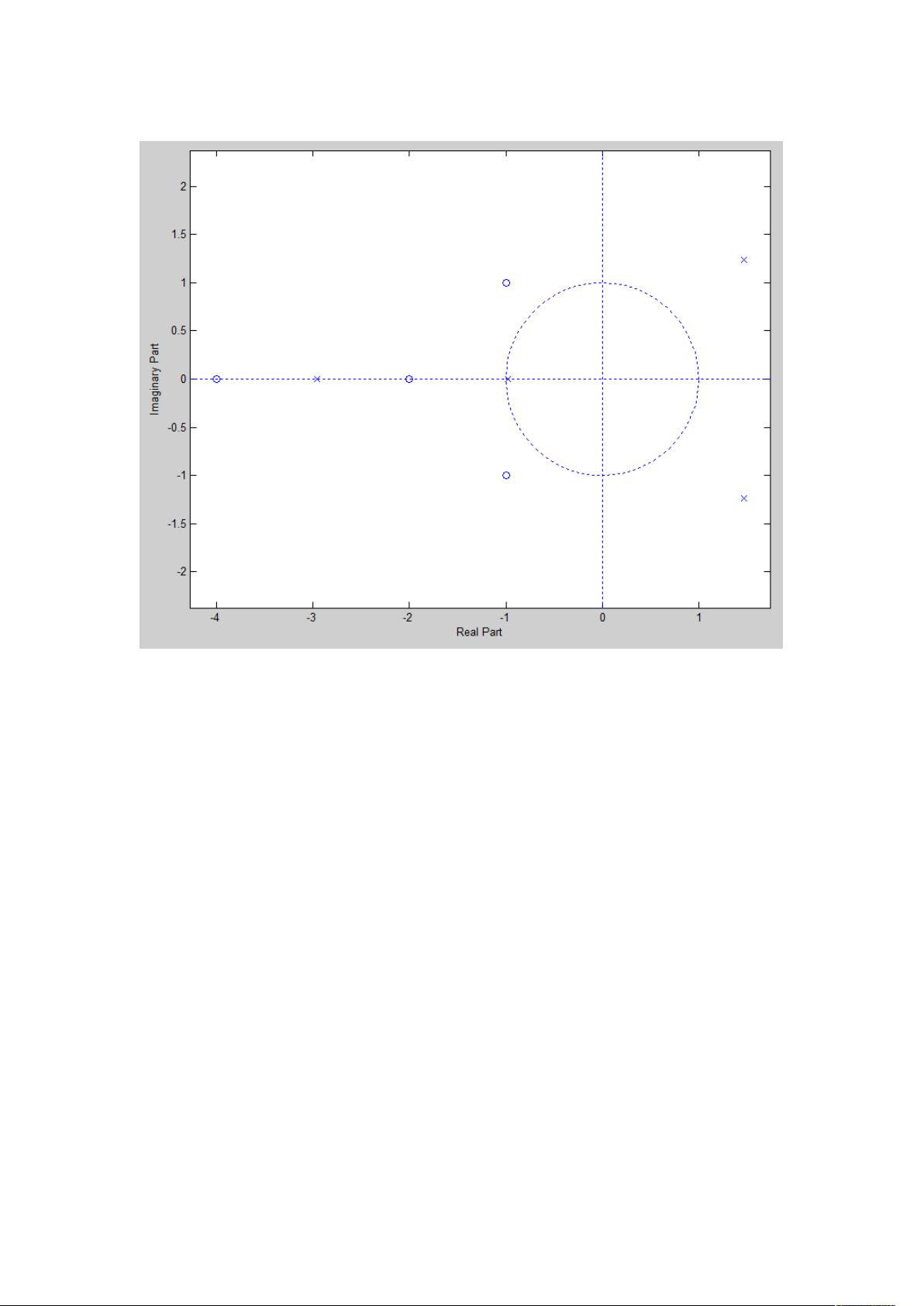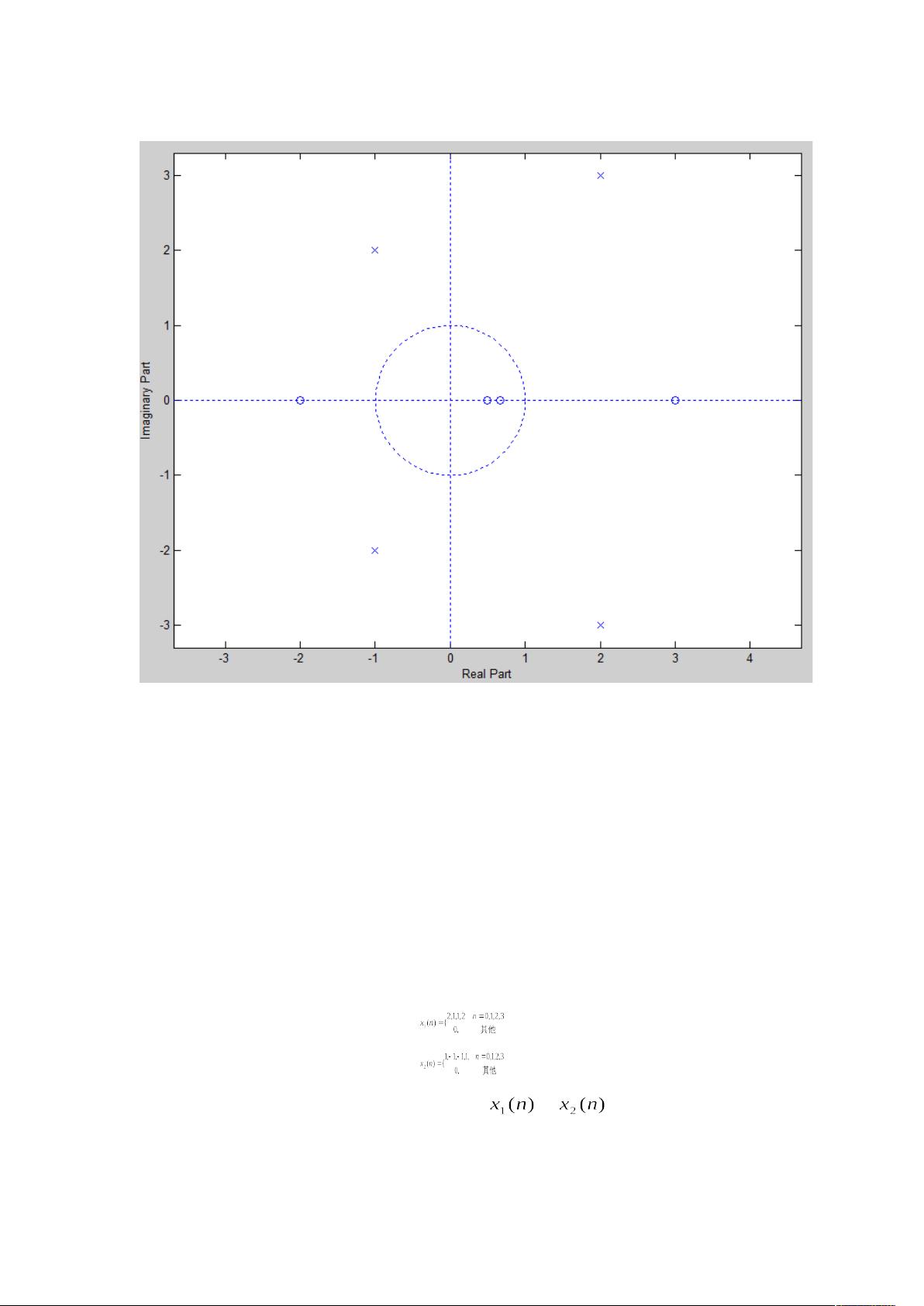 最后，案例3.47涉及Z变换和滤波器的稳定性分析。Z变换是离散时间信号分析的基础工具，通过`zplane`函数可以得到系统的极点和零点分布，从而判断其收敛域。在这个例子中，识别了四个可能的收敛域，这对应于滤波器的不同稳定状态，对于滤波器的设计和性能评估具有指导意义。 这些案例涵盖了数字信号处理的核心概念，包括脉冲响应、卷积运算、噪声干扰的模拟以及滤波器稳定性的分析，这些都是理解和应用数字信号处理技术的关键点。通过MATLAB的可视化工具，我们可以更直观地理解这些复杂的数学概念，并将它们应用于实际的信号处理问题中。