空间解析几何:向量代数与线性运算
需积分: 9 130 浏览量
更新于2024-07-23
1
收藏 722KB PDF 举报
"该资源主要涉及空间解析几何与向量代数,是高数课程的第七章内容,特别对理解并深入学习OpenGL图形算法有帮助。解析几何是研究空间几何问题的一种数学方法,通过代数手段来处理几何问题。本章节涵盖了向量的基本概念、线性运算以及数与向量的乘法。"
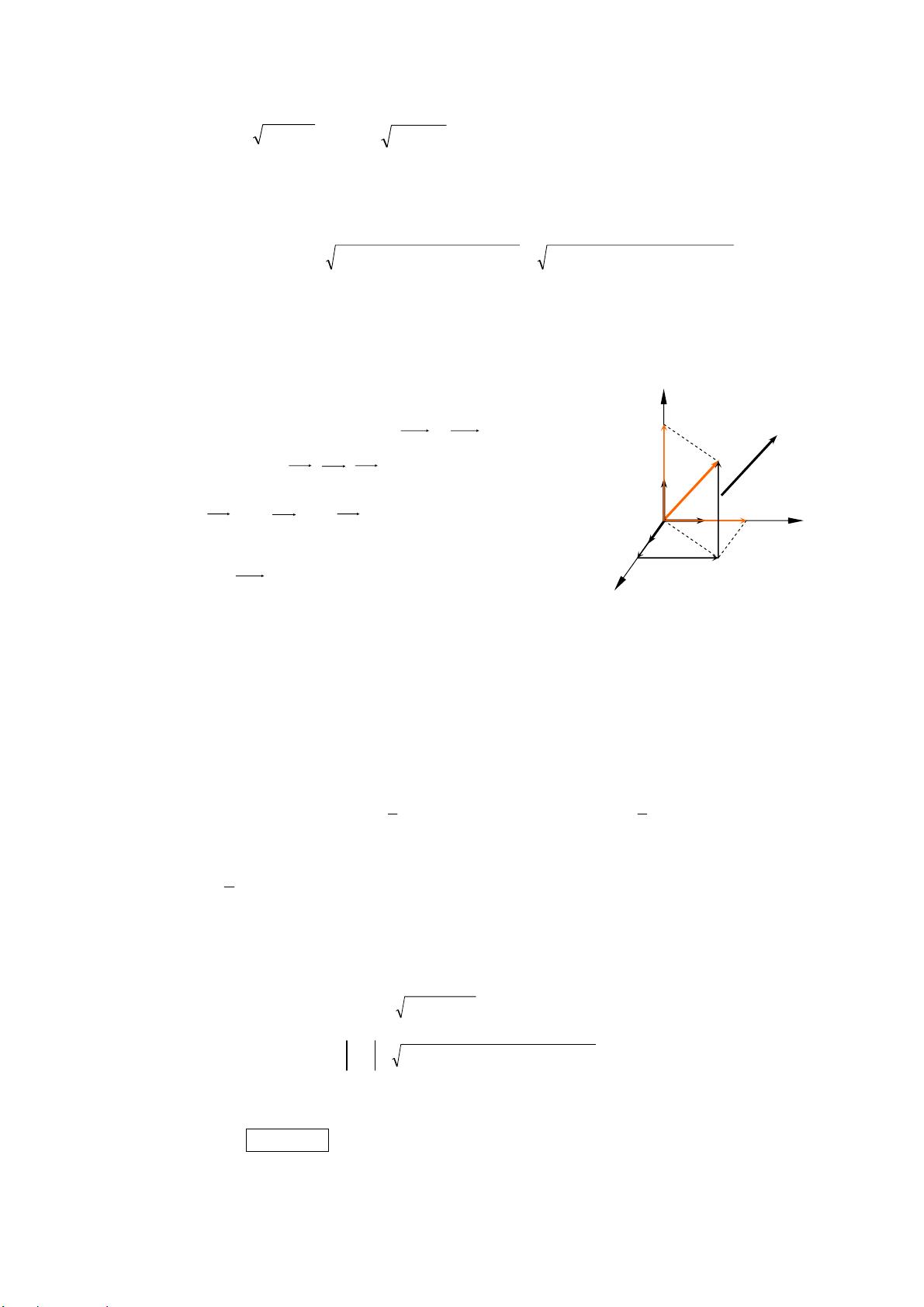
在空间解析几何中,向量是一个关键概念,它不仅具有大小(模),还具有方向。向量通常用小写黑体字母表示,如a或b,其模长用|a|表示。模长为1的向量被称为单位向量,记为e,模长为0的向量称为零向量,记为o,零向量的方向可以任意设定。向量的相等意味着它们的模长相同且方向一致,相反向量则是模长相等但方向相反的向量。
向量的线性运算包括向量的加法和减法。向量加法可以通过平行四边形法则实现,即将两个向量的起点放在同一位置,然后从第一个向量的起点到第二个向量的终点画一条直线,这条直线形成的向量就是两个向量的和。向量减法则是加法的逆运算,可以理解为加上被减向量的相反向量。此外,向量加法满足交换律(a+b=b+a)和结合律((a+b)+c=a+(b+c))。
向量与数的乘法,也称为标量乘法,其中实数λ乘以向量a的结果是一个新向量λa。这个新向量的模长是原向量模长的λ倍,方向与原向量方向一致(当λ>0)或相反(当λ<0)。标量乘法的性质包括分配律(λ(a+b)=λa+λb和(λ+μ)a=λa+μa)和标量乘积的结合律((λμ)a=λ(μa))。
向量代数在空间解析几何中的应用广泛,例如在物理学中,可以用向量表示力的作用,通过向量加法求合力。在计算机图形学中,如OpenGL,向量代数是基础,用于描述三维空间中的对象位置、运动和旋转。理解并掌握这些基本概念和运算是进行更复杂的空间计算和图形编程的前提。
2017-10-20 上传
2019-06-09 上传
2022-07-14 上传
152 浏览量
2010-07-30 上传
2009-04-22 上传
2021-09-27 上传