算法设计策略：动态规划与FFT在矩阵链乘与多项式相乘中的应用

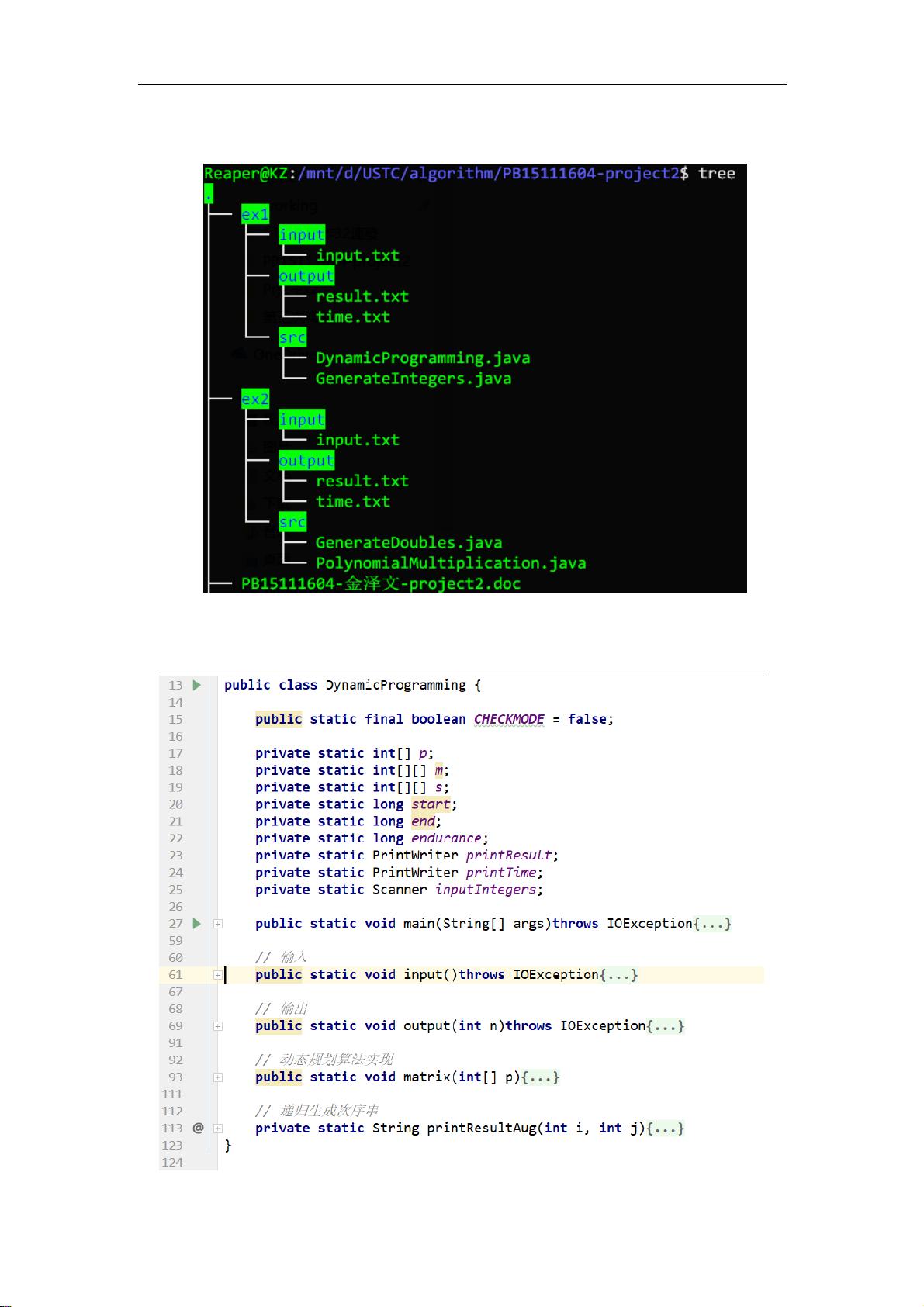
"PB15111604-金泽文-project21" 这篇文档描述了一个关于算法设计策略的实验项目，主要包括两个部分：矩阵链乘问题的动态规划解决方案和快速傅里叶变换（FFT）在多项式相乘中的应用。实验要求针对不同规模的数据进行性能测试，并绘制时间曲线以对比算法效率。 1. 矩阵链乘问题 是一个经典的动态规划问题，目标是找到一系列矩阵相乘的最优顺序，以减少乘法操作的次数。在实验中，需要对不同大小的矩阵链（5x10x20x30）生成随机规模，并利用动态规划算法求解最优乘法次序。动态规划的核心在于构建一个二维表s和m，其中s[i][j]记录了矩阵i到j的最优乘法路径，m[i][j]记录了相应的最小代价。实验结果需符合教材上的预期，并通过正则表达式处理输出，使其更易读。 2. 快速傅里叶变换（FFT）是一种高效的计算复数或实数序列离散傅里叶变换的算法。在实验的第二部分，要求实现FFT算法来计算两个多项式的乘积。对于不同大小的多项式（4, 16, 32, 60），从输入文件读取随机生成的系数，扩展为2的幂次以适应FFT。值得注意的是，当n不是2的幂时，需要特殊处理。实验还包括与传统乘法方法的时间比较，以展示FFT的效率优势。 3. 实验环境 指定了Java SE 8作为编程语言，以及具有16GB内存和2.3GHz主频的计算机。实验代码应能在Linux环境下编译运行，并通过设置CHECKMODE为true来检查正确路径。 4. 实验过程 包括随机数生成，数据输入，算法实现和结果验证。在矩阵链乘部分，随机数写入input.txt文件；在FFT部分，除了基本的输入和计算，还需要处理非2的幂次的情况。实验结果将记录算法运行时间并绘制时间曲线，以展示随着数据规模增长，算法性能的变化。 5. 总结 这个实验项目旨在加深对动态规划和FFT算法的理解，同时也关注算法在实际应用中的性能表现。通过比较不同规模下的运行时间，可以评估算法的复杂度，并理解其在大规模数据处理中的优势。实验结果的验证确保了算法的正确性，而时间曲线则提供了算法效率的直观展示。