递归与分治算法详解：从汉诺塔到八皇后

"该资源是一个关于递归、分治与归并策略的PPT教程，主要探讨了递归和分治方法在解决算法问题中的应用，包括汉诺塔、八皇后问题等经典实例，并提到了快速排序和归并排序等算法。" 递归是一种解决问题的方法，它将大问题分解为相同或相似的小问题来解决。递归定义的特点是问题的解决方案依赖于规模更小的同类问题的解。例如，函数f(n)的值可以通过f(n-1)的值来计算，直到达到基本情况（如n=0）。这种思维方式在计算机科学中非常常见，因为许多复杂的问题都可以通过简化规模来解决。 分治策略是递归的一种应用，它将一个大问题分解为两个或更多的相同或相似的子问题，直到这些子问题变得足够简单，可以直接求解，然后合并这些子问题的解以获得原问题的解。分治法常用于排序问题，如快速排序和归并排序。 1. 汉诺塔问题是一个经典的递归问题，目标是将所有盘子从一根柱子移动到另一根柱子，遵循大盘子不能放在小盘子上的规则。解决这个问题需要递归地将顶部的若干盘子移动到中间柱子，然后移动最底部的大盘子，最后将剩余的盘子从中间柱子移动到目标柱子。 2. 八皇后问题是一个著名的分治与回溯问题，要求在8x8的棋盘上放置8个皇后，使得它们不能互相攻击。这个问题通常使用递归回溯算法解决，通过尝试在每一行放置一个皇后并检查是否违反规则，如果违反则回溯到上一行重新尝试。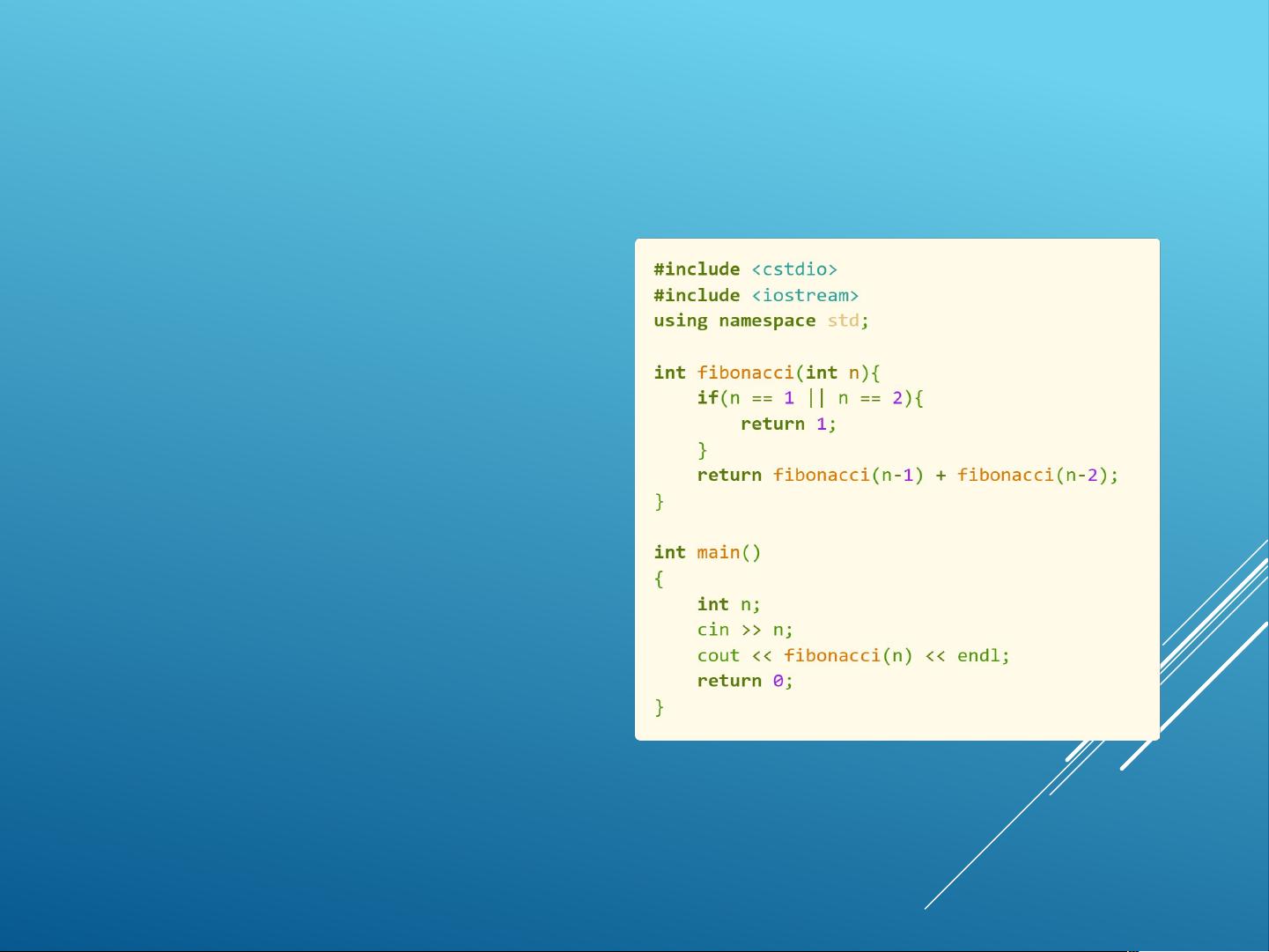 3. 斐波那契数列是递归的典型例子，每个数字是前两个数字的和。递归求解斐波那契数列虽然直观，但效率较低，因为存在大量的重复计算，更适合使用动态规划优化。 4. 快速排序是一种高效的排序算法，基于分治思想。首先选择一个“切分元素”，将数组分为两部分，左边的元素小于切分元素，右边的元素大于切分元素，然后对这两部分递归进行快速排序，最后合并结果。 5. 归并排序是另一种分治算法，它将数组分为两半，分别排序，然后合并两个已排序的子数组。归并排序保证了稳定的排序效果，适用于大规模数据。 递归、分治和归并是解决复杂计算问题的重要工具，它们在算法设计和数据结构中起着关键作用，帮助我们高效地处理各种问题。本PPT教程适合初学者入门，通过实例讲解了这些概念和技术。