颜色与物质浓度辨识：多元回归分析在MATLAB中的应用

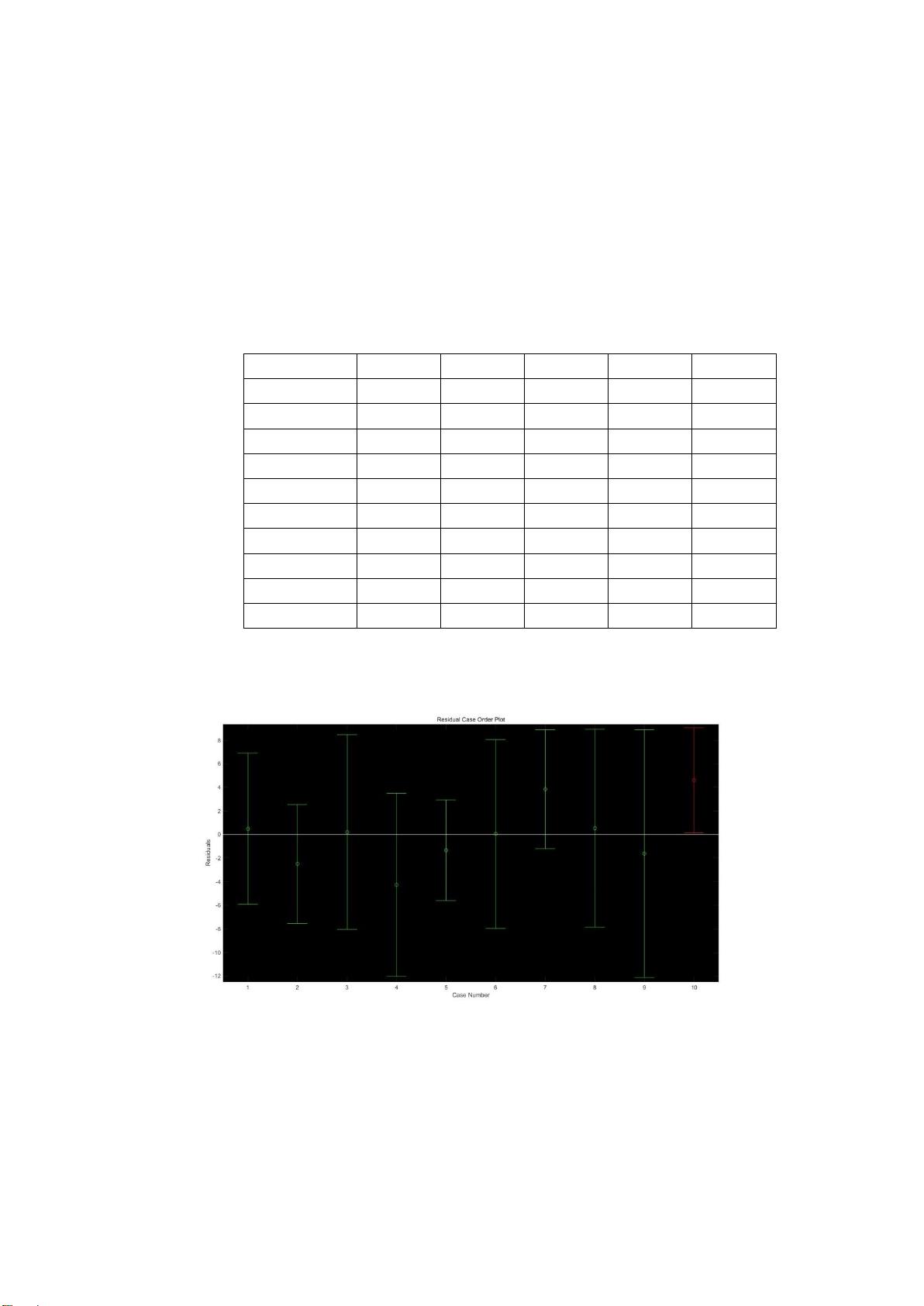
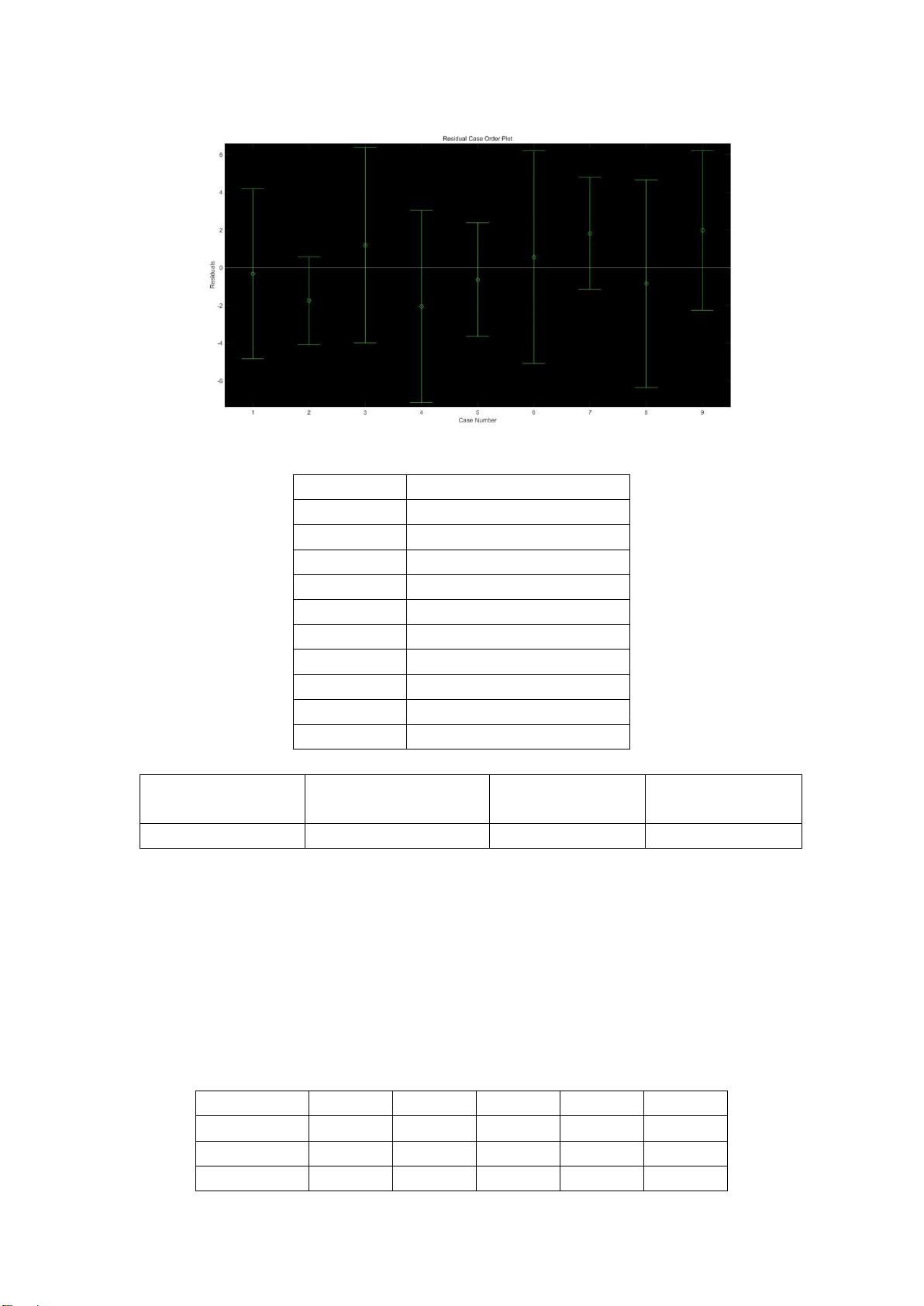
"颜色与物质浓度的辨识问题研究，多元回归分析，线性与非线性模型，误差分析，MATLAB应用，数据评价准则" 在本研究中，主要探讨了颜色与物质浓度之间的辨识问题，特别是在化学检测领域，比色法是一种常见的浓度测定方法。通过对溶液的色度值与相应物质浓度的实验数据进行分析，可以建立数学模型来预测未知浓度。本文主要涉及了两个关键的统计分析工具：多元线性回归和多元非线性二次回归，并使用MATLAB的统计工具箱进行建模。 首先，研究人员通过多元线性回归分析来寻找颜色读数与物质浓度之间的关系。利用MATLAB的Regress函数计算回归系数和置信区间，同时进行残差分析，以确保模型的稳定性和可靠性。通过F检验、相关系数R、P值和估计误差方差S这四个准则评估模型的性能。例如，在对不同物质（如组胺、溴酸钾、奶中尿素、硫酸铝钾和工业碱）的数据分析中，这些准则用于判断数据的优劣并排序。 然而，对于某些情况，线性模型可能无法完全捕捉到数据的复杂性。当线性模型的残差较大，表明拟合效果不佳时，研究人员转向非线性回归模型。这里，他们采用了非线性二次回归模型，利用rstool函数进行建模。通过比较剩余标准差和残差，发现在二氧化硫浓度问题上，非线性二次回归模型显著优于线性模型，其预测精度大大提高。 此外，研究还关注了模型构建中的两个关键因素：颜色维度和数据量。降低颜色维度可以简化模型，但可能会影响准确性。而数据量的多少则直接影响模型的稳定性和泛化能力。通过层次分析法，得出数据量和颜色维度对模型影响的权重，分别为0.414和0.586，强调了颜色维度的重要性。 这篇研究展示了如何利用MATLAB进行多元回归分析，以解决颜色与物质浓度的关系问题。无论是线性还是非线性模型，都需要结合实际问题和统计学指标来选择和优化。通过这种方法，可以提高比色法的精确度和可靠性，为化学检测提供更为准确的浓度预测。