MATLAB在线性系统理论中的建模与仿真应用

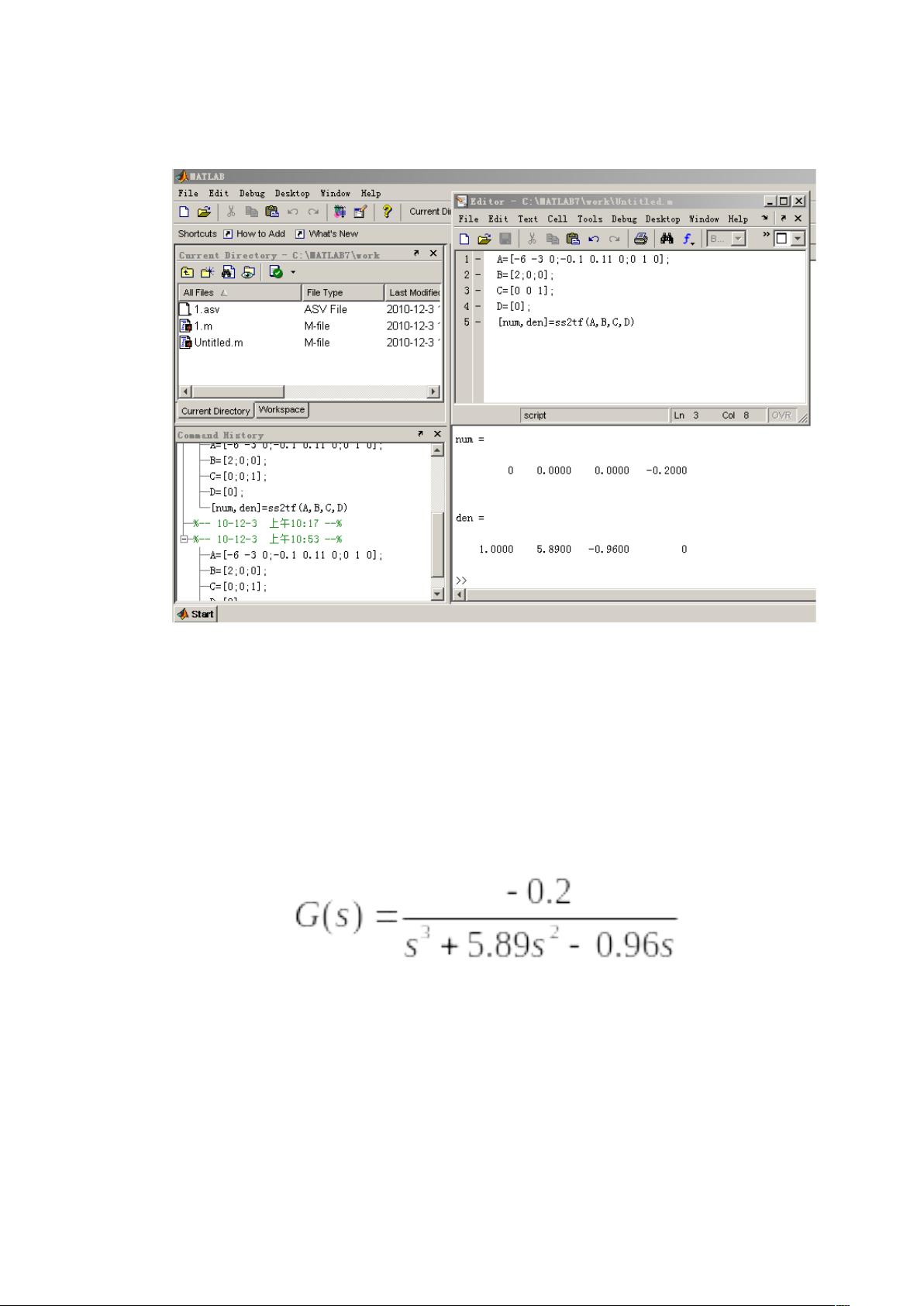
"线性系统理论MATLAB_仿真" 线性系统理论是自动化和控制系统领域中的核心概念，它涉及系统的建模、分析和控制设计。MATLAB作为一种强大的数值计算和仿真工具，广泛应用于线性系统理论的学习和研究。在这个文档中，我们将深入探讨如何使用MATLAB进行线性系统的建模、仿真以及性能分析。 首先，线性系统的建模通常涉及传递函数模型和状态空间模型。在MATLAB中，可以通过`tf`函数创建传递函数模型，而`ss`函数则用于构建状态空间模型。例如，对于一个电枢控制的直流电动机模型，状态变量可以选择为回路电流和电枢旋转角速度，通过解析微分方程得到相应的状态方程和输出方程。文档中给出了具体的数学表示，并指定了电机的参数值，以便在MATLAB中进行仿真。 接着，MATLAB提供了方便的工具进行模型转换。例如，通过`ss2tf`函数可以从状态空间模型转换为传递函数模型，反之亦然。这样，我们可以方便地在不同模型之间切换，以适应不同的分析需求。 然后，使用MATLAB进行系统分析是非常直观的。比如，通过绘制系统响应的图形，可以直观地了解系统的行为。文档中提到了单位阶跃响应的仿真，这通常用来评估系统的瞬态性能。MATLAB的`step`函数可用于绘制这种响应曲线。 此外，系统能控性和能观性的判断是系统设计中的关键步骤。在MATLAB中，`ctrb`函数可以计算能控矩阵，帮助判断系统的能控性；而`obsv`函数则用于计算能观矩阵，评估能观性。如果能控矩阵或能观矩阵的秩等于系统状态的阶数，那么系统就是能控或能观的。同时，MATLAB还支持将系统转换为能控或能观标准型，这对于控制器设计和状态观测器设计非常有用。 最后，系统稳定性是衡量系统性能的重要指标。MATLAB提供了多种工具，如根轨迹、频率响应和劳斯判据等，来分析线性系统的稳定性。例如，`rlocus`函数可以绘制根轨迹图，`bode`函数用于绘制频率响应图，而`lyap`和`hess`函数可以帮助计算系统矩阵的特征值，从而判断系统的稳定性。 MATLAB为线性系统理论的实践提供了强大的支持，不仅简化了模型建立和转换的过程，还使得系统分析和设计变得更加直观和高效。通过上述方法，学习者可以深入理解线性系统的基本概念，并应用到实际问题的解决中。