中国居民消费函数的序列相关检验与修正实证研究

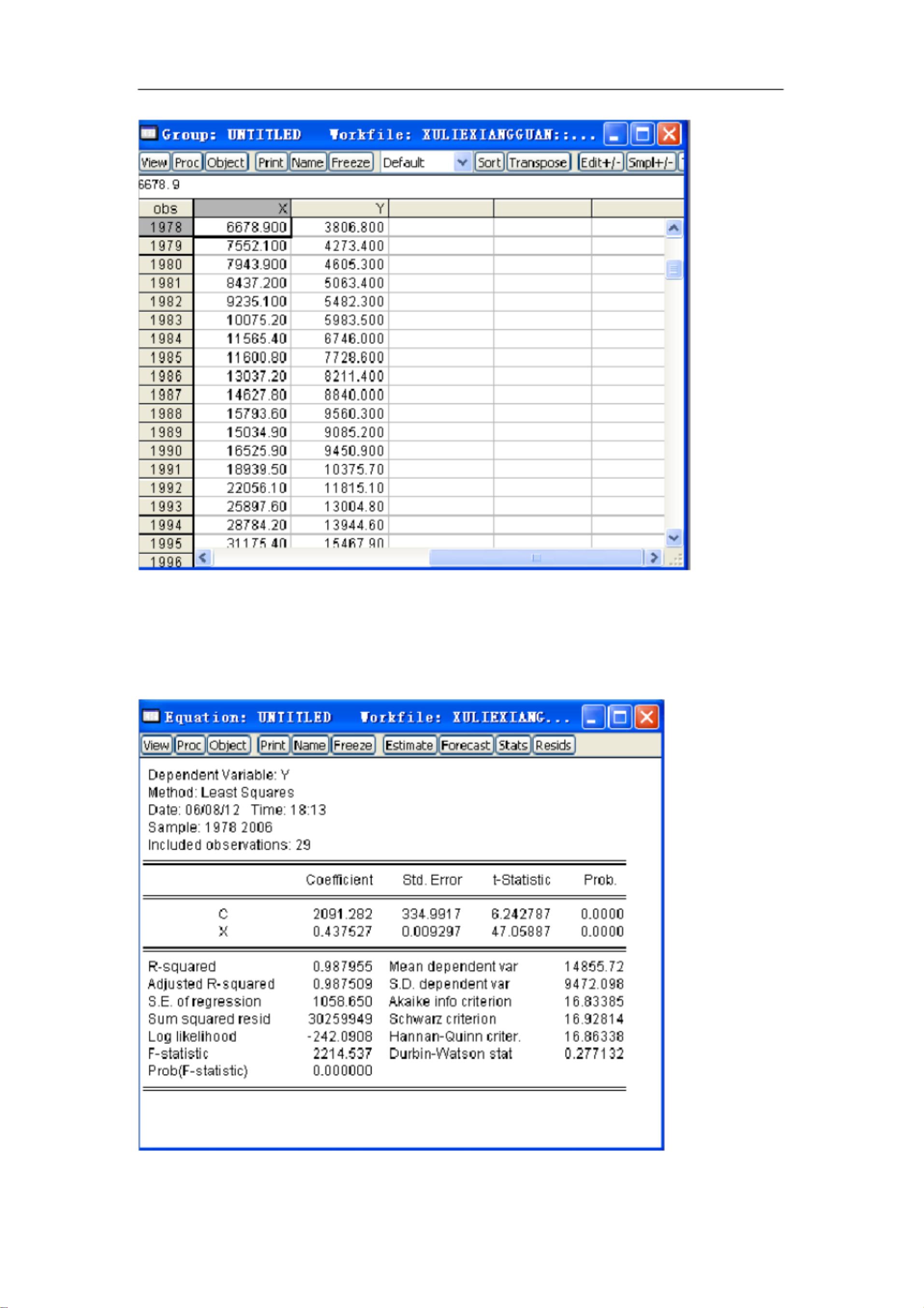
"序列相关的检验和修正是一种统计学方法，用于处理时间序列数据中可能存在的自相关性问题。在经济、金融和宏观经济分析中，序列相关性是指一个变量的当前值与其过去值之间存在显著关联，这可能影响到估计模型参数的准确性，特别是当采用普通最小二乘法（OLS）进行回归分析时。如果不考虑这种关系，可能会导致错误的预测和无效的假设检验结果。 在给出的例题中，是中国居民总量消费函数的数据，包含了1978年至1994年期间的数据，包括GDP（国内生产总值）、CONS（消费品支出）、CPI（消费者价格指数）、TAX（税收）、GDPC（国内生产净值）、X和Y等变量。这些数据被用于构建消费函数模型，可能涉及消费与收入、物价水平、税收等因素的关系研究。然而，由于时间序列数据可能存在长期趋势或季节性变化，序列相关性检测是必要的，以确保模型的有效性和可靠性。 在实际操作中，可能使用Ljung-Box检验、Durbin-Watson检验或Phillips-Perron测试来确认序列相关性。如果发现序列相关，可以采取以下几种修正方法： 1. 差分法（Differencing）：通过减去前一时期的值来消除自相关，适用于趋势型序列相关。 2. 广义矩估计（Generalized Least Squares, GLS）：引入自回归项或移动平均项（ARMA模型），对模型进行修正。 3. 广义差分法（Generalized Difference Estimation, GDE）：在差分的基础上，考虑滞后项的影响。 4. Newey-West校正：针对动态面板数据，通过调整估计标准误差，降低自相关影响。 5. 广义自回归条件异方差模型（Generalized Autoregressive Conditional Heteroskedasticity, GARCH）：适用于金融数据，考虑了时间序列数据的波动性。 在进行修正后，模型的估计将更为稳定，预测能力也会提高，这对于理解和预测经济行为、政策制定以及经济理论检验都至关重要。在分析中国居民总量消费函数时，理解并处理序列相关性对于得出更准确的结论具有重要意义。"