线段树高级应用探讨

"吉司机线段树吉如一原文" 这篇文档主要讨论的是吉司机线段树，一种在算法竞赛和编程中用于高效处理区间数据结构的问题。线段树通常用于处理动态范围查询和更新的问题，例如区间求和、区间最小值等。作者通过一个具体的例子来阐述线段树在面对特定问题时的拓展应用。 首先，文章提到在今年的清华大学集训中，出现了一道涉及线段树的题目，但在讲解过程中发现有人对于区间版本的线段树不熟悉。因此，作者决定深入研究这类问题，并制作了一个PPT来分享他们的发现。他们指出，虽然线段树在信息学奥林匹克竞赛（OI）中常常被视为基础工具，但其实存在一些非平凡的线段树问题值得探索。 接着，作者介绍了问题的背景：给定一个数列A，需要处理m次操作，操作包括将区间[l, r]内的所有元素变为最小值min(Ai, x)，以及查询区间[l, r]内所有元素的和。对于小规模数据（n, m ≤ 50,000），可以直接使用线段树，但对于大规模数据（n, m ≤ 500,000），简单的线段树无法胜任。 然后，作者提供了一个朴素的O(n²logn)解决方案，即暴力查找每个区间内的最大值，如果最大值大于x，则修改该位置的值。但这种方法效率低下，不适合大数据量。 为优化这个过程，作者提出了增强线段树的概念，为每个节点维护区间最大值mx、最大值出现的次数t、区间次大值se以及区间和sum。当需要执行区间取min操作时，根据mx、se和x的关系进行不同处理。如果mx <= x，则无需修改sum；如果se < x < mx，需要修正sum；然而，当x <= se < mx时，处理变得复杂，需要递归地遍历子节点。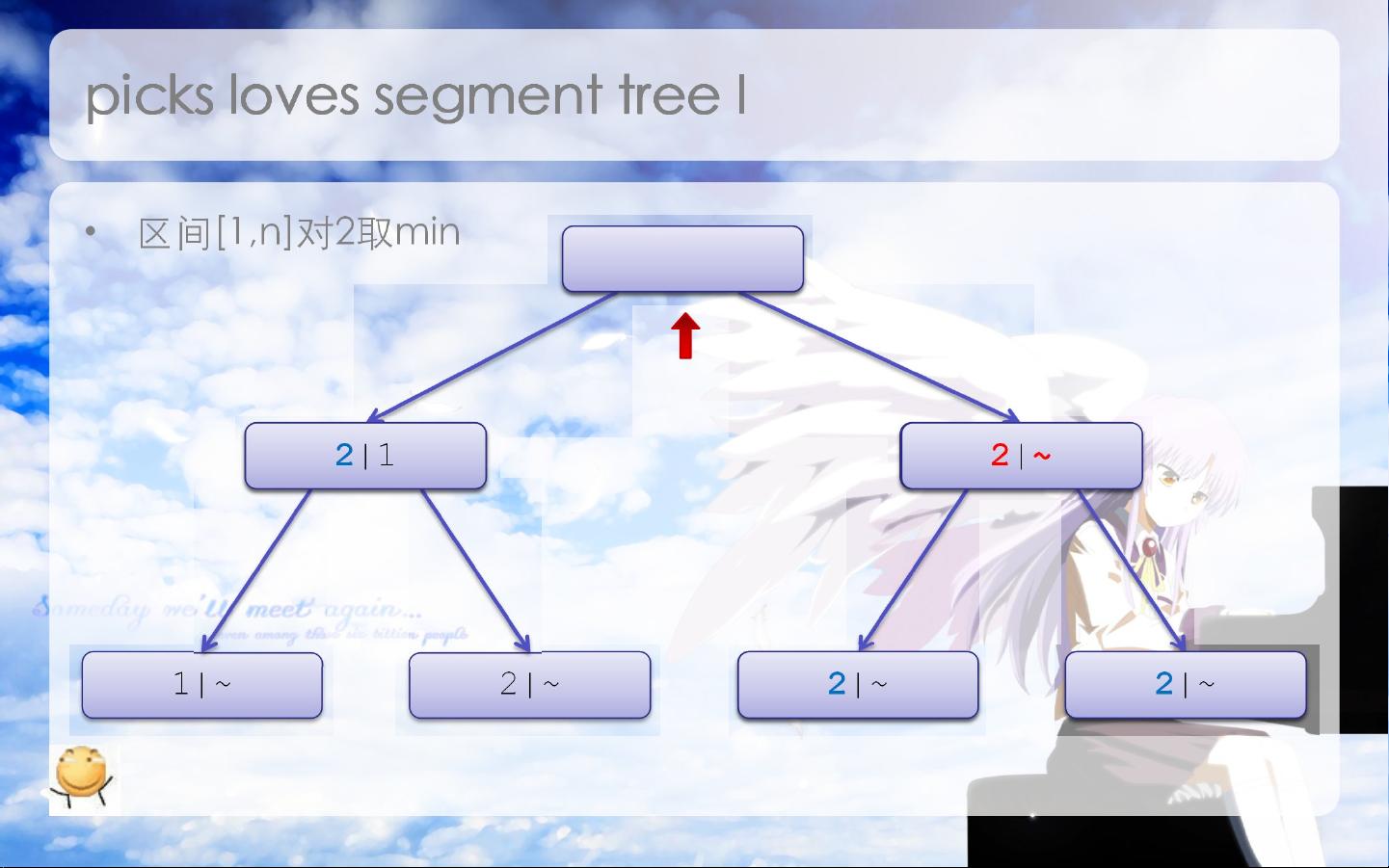 通过实例展示了区间[1, n]对2取min的过程，可以看到线段树如何有效地更新和查询区间状态。这种方法虽然增加了实现的复杂性，但能显著提高算法效率，适用于处理大规模数据的区间操作。 这篇文档探讨了线段树在处理区间取最小值问题时的扩展应用，强调了线段树并非只能解决基础问题，还可以应对更复杂的场景。通过增强线段树的数据结构和递归处理，能够解决大规模数据的动态更新和查询需求。对于信息学竞赛选手和算法工程师来说，理解并掌握这种扩展是提高算法能力的重要一步。