分段函数详解及实例：求值、画图与性质

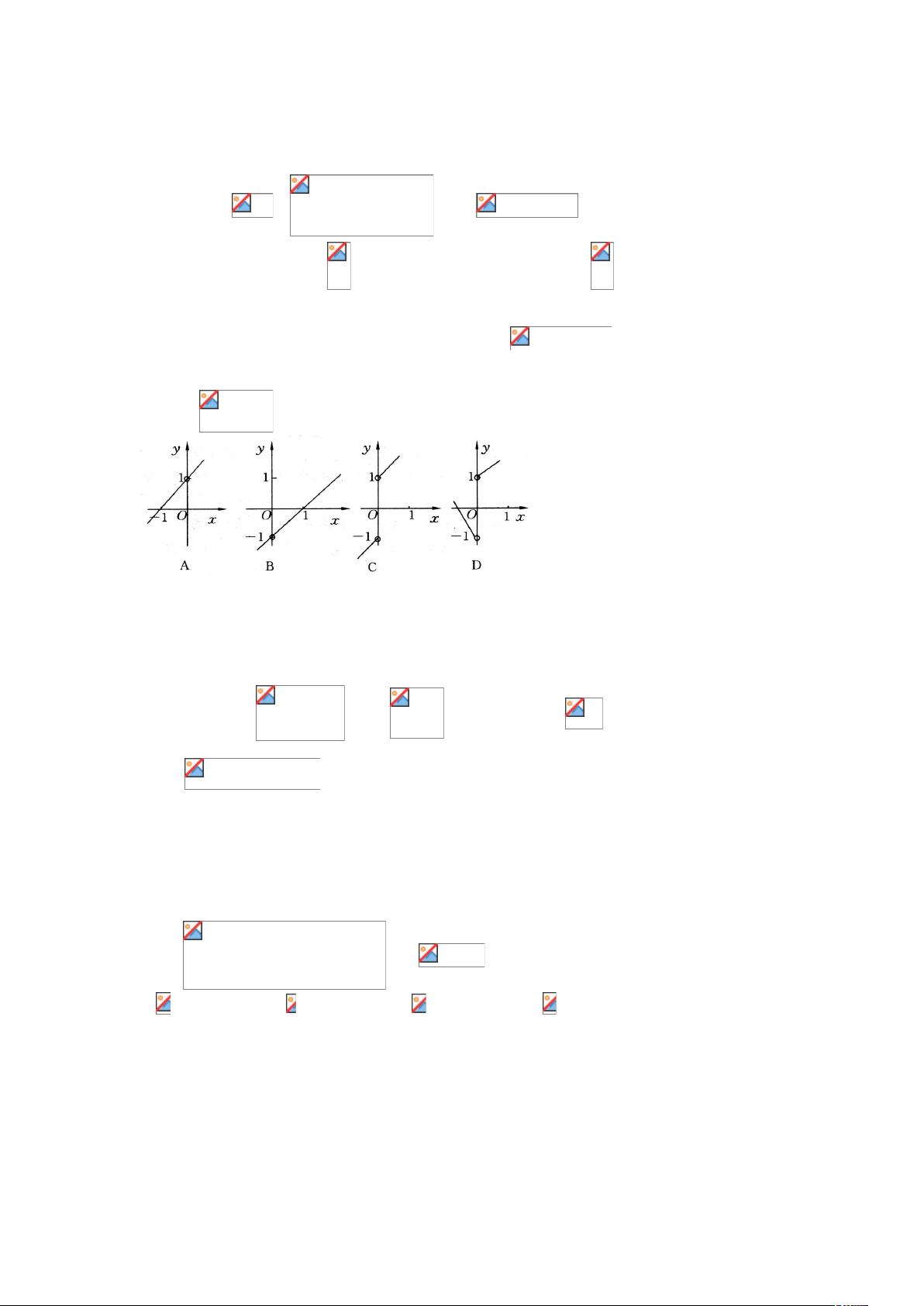
分段函数是一类特殊的数学函数，其特点是根据自变量的不同取值范围，函数的解析式在不同的区间内有不同的表达。以下是一些关于分段函数的练习题及其解答： 1. 题目要求计算分段函数 [pic] 在特定点的值，其中 [pic] 表示在x=0时应用第一个函数，x=-1时应用第二个函数。通过代入计算，当x=0时，[pic]=3；当x=-1时，[pic]=9。所以答案是C，3。 2. 考察分段函数的图像，函数 [pic] 包含两个部分，当x>0时，y=x+1；当x<0时，y=x-1。图形上，这会形成一个V形，选项C符合图示特征。 3. 考查函数是否表示同一个函数，主要看定义域、值域和对应关系。①中f(x)和g(x)都表示绝对值，定义域和对应关系相同，是同一函数；②中两函数在x=0处解析式不同，不是同一函数；③中f(x)和g(x)都是线性函数，但斜率不同，不是同一函数；④中两函数在定义域{-1,1}上值域相同，也是同一函数。因此，正确答案是A，①③。 4. 对于分段函数 [pic]，当x=2时，[pic]=log3(2^2-1)=1，再将f(2)带入原函数得到f(f(2))=f(1)，进一步计算得出结果为2。所以选项C是正确的。 5. 这个题目涉及分段函数的递推关系。定义在实数集R上的函数 [pic] 满足 [pic]，通过递推可以得出f(3) = f(2) - f(1)，然后利用初始条件解出f(0)和f(1)，最终计算得到f(3) = -f(0) = -log2(4-0) = -2，选择B。 6. 题目没有给出具体的分段函数，但从提示看，可以通过代入法直接求解[pic]的值。如果[pic]=8，代入相应区间内的函数解析式，可以求得x的值。由于没有给出具体函数，无法给出确切答案，但解题思路是明确的。 总结，分段函数练习题主要考察理解函数在不同区间内的定义和行为，以及运用这些定义解决实际问题的能力。在解题过程中，需要注意区分不同区间下的函数解析式，并能准确地计算和绘制图像。理解函数的三要素——定义域、值域和对应关系——是判断两个函数是否为同一函数的关键。