图论基础：欧拉回路与图的存储结构

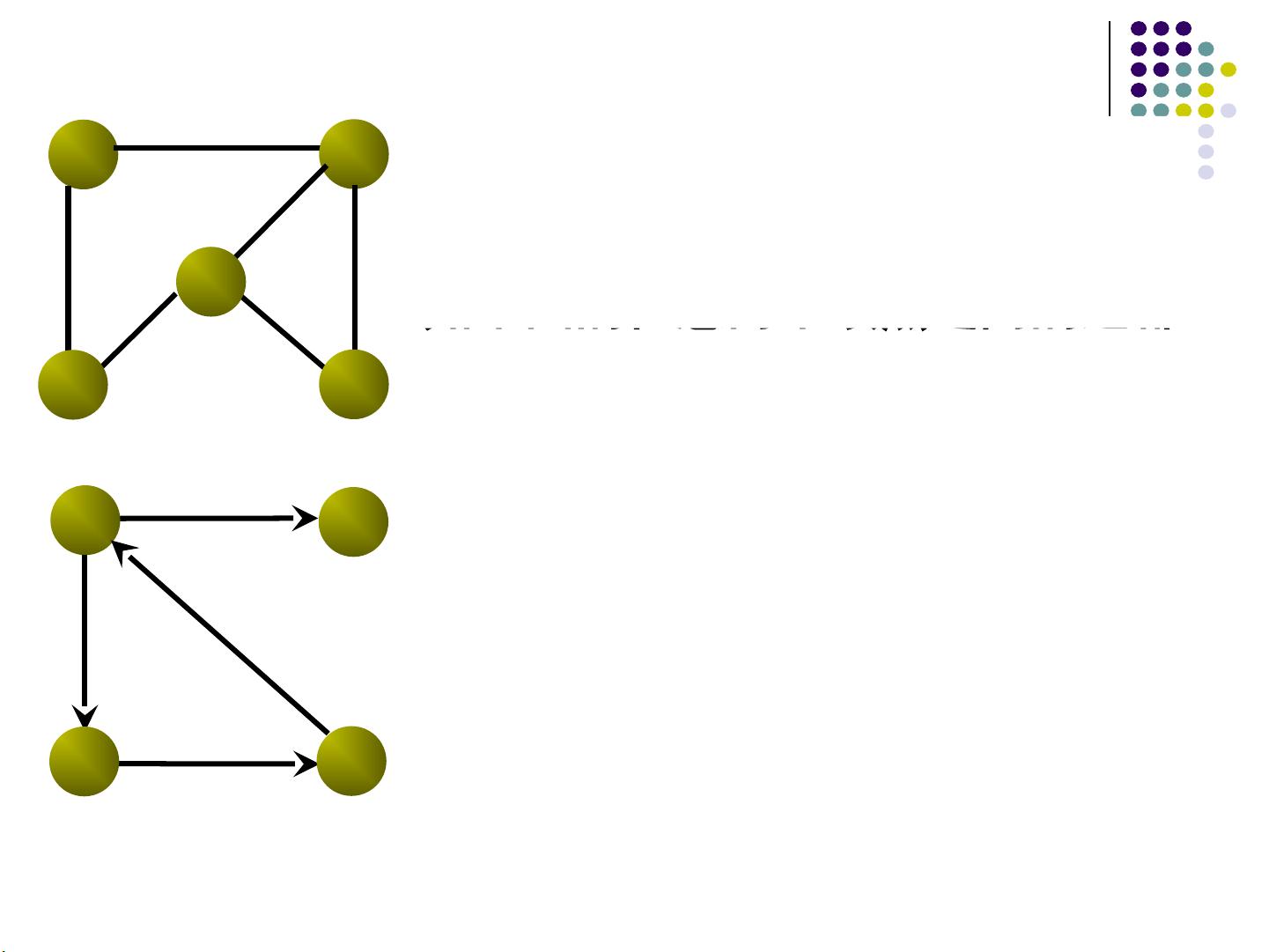
"数据结构图的定义和存储" 本文主要介绍了图论的基础知识，包括图的定义、存储结构以及相关的概念，如欧拉回路、哈密尔顿回路和四色猜想。图论是由瑞士数学家欧拉创立的，他对哥尼斯堡七桥问题的解答开启了这一领域的研究。 1. 图的定义：图是一种抽象的数据结构，由顶点（vertices）和边（edges）组成，用于表示对象之间的关系。在哥尼斯堡七桥问题中，城市和桥梁被抽象为顶点和边，展示了图如何模型化现实世界的问题。 2. 欧拉回路：欧拉回路是图中一种特殊的路径，从一个顶点出发，沿着边行走，每条边恰好经过一次并返回起点。欧拉回路的存在与否可以通过判断图中奇数度顶点的数量来确定。 3. 哈密尔顿回路：哈密尔顿回路与欧拉回路不同，它要求从图的一个顶点出发，经过每个顶点一次并回到起点，但不必经过每条边。哈密尔顿回路在旅行商问题中有着实际应用，寻找最短的哈密尔顿回路是NP完全问题。 4. 四色猜想：这是一个著名的图论问题，指出任何平面图都可以用不超过四种颜色给各个区域染色，使得没有两个相邻的区域颜色相同。1976年，这个问题通过计算机辅助证明得到解决。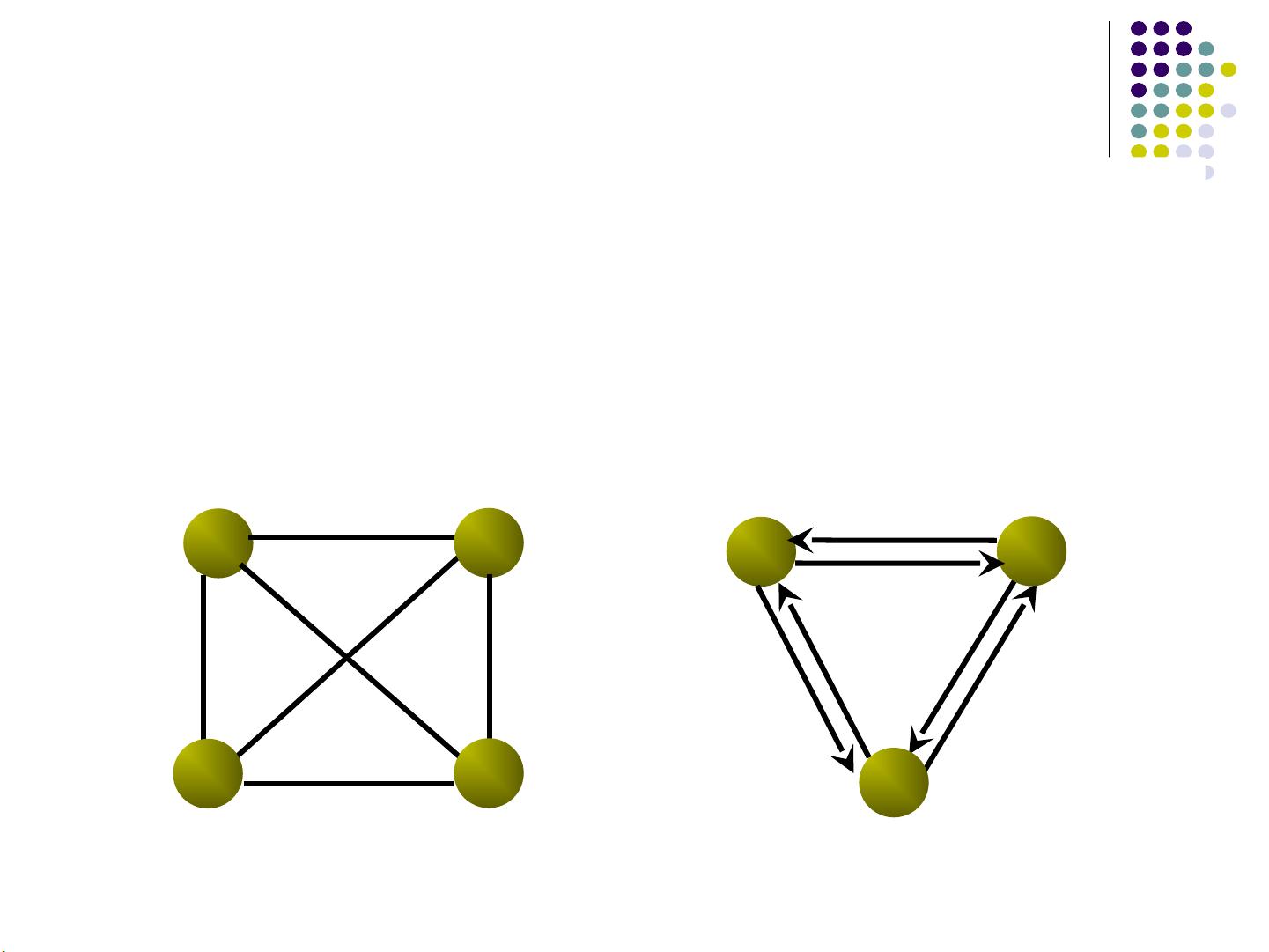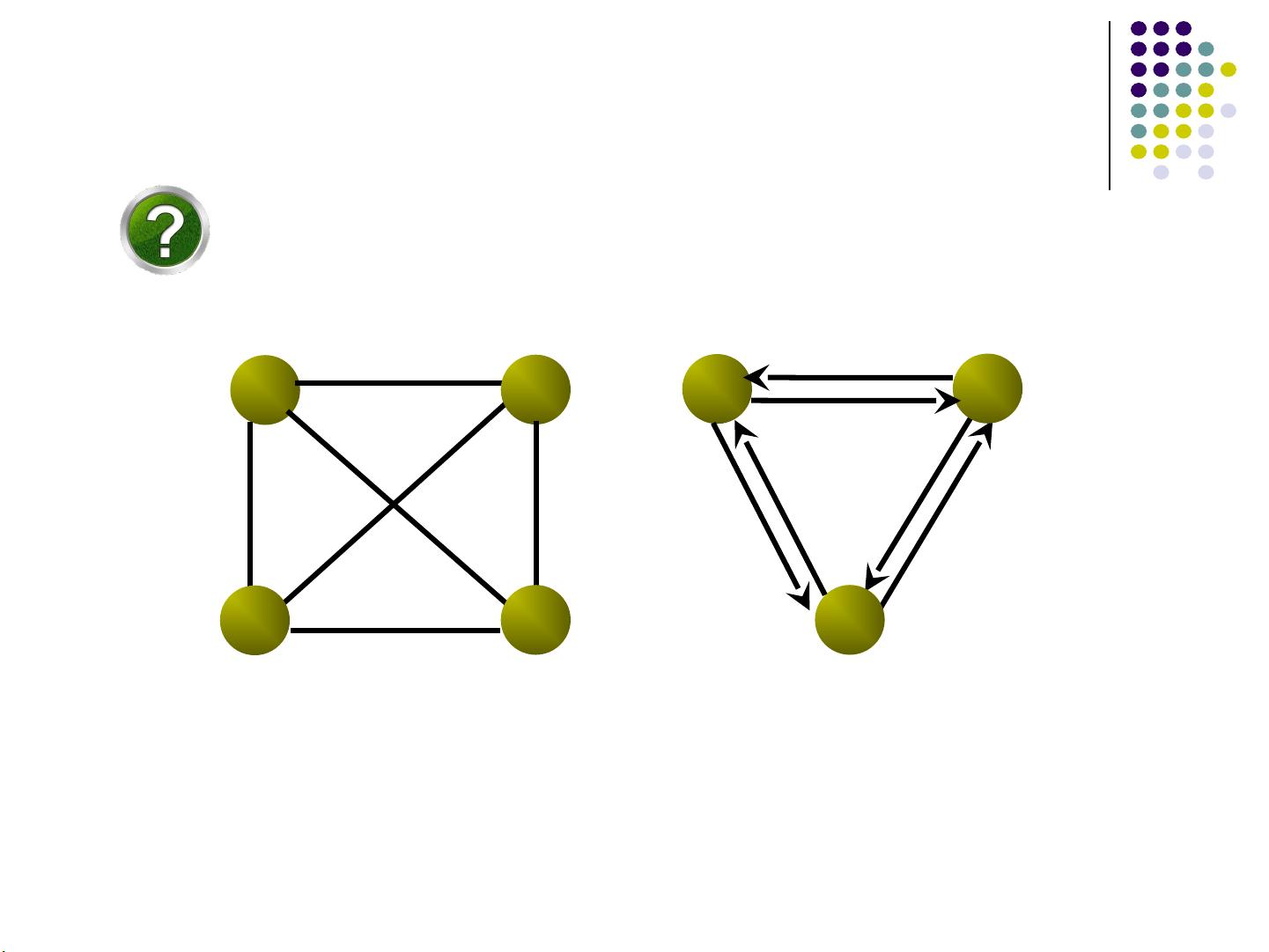 5. 图的存储结构：图的存储通常有两种方式，邻接矩阵和邻接表。邻接矩阵是一个二维数组，用于表示任意两个顶点之间是否存在边；邻接表则为每个顶点维护一个边的列表，适用于稀疏图（边数远小于顶点数的平方）。 6. 图的遍历：图的遍历主要有深度优先搜索（DFS）和广度优先搜索（BFS）。DFS是从一个顶点出发，尽可能深地搜索图的分支，而BFS则是从起点开始，逐层探索所有相邻顶点。 学习重点在于理解图的存储结构对算法效率的影响，以及掌握DFS等遍历方法的实现。在实际问题求解中，选择合适的存储结构和算法至关重要。图论在计算机科学中有着广泛应用，如网络路由、社交网络分析、物流规划等。随着计算机技术的发展，图论已成为数学和计算机科学中的一个重要分支。