机器人DH坐标系建立与运动学解析

"本资源详细介绍了机器人DH坐标系的建立方法，涵盖了不同情况下的建系技巧，包括平移和旋转的组合。主要内容涉及正逆运动学的求解基础，坐标变换，以及各种关节类型和杆件构形。" 在机械臂的运动学中，DH坐标系（Denavit-Hartenberg Parameters）是一种广泛使用的表示方法，用于描述机器人各关节和杆件之间的几何关系。DH坐标系的建立旨在明确机器人各个部件在空间中的相对位置，从而能够通过关节角的计算得出末端执行器的位置（正运动学），或者反过来，根据末端执行器的目标位置推算出所需的关节角（逆运动学）。 正运动学是将关节变量转换为末端执行器在空间的位置和姿态，而逆运动学则是解决相反的问题，即给定末端执行器的期望位置和方向，求解各关节应具有的角度。DH坐标系通过一系列的坐标变换矩阵实现这些计算。 在建立DH坐标系时，需要考虑以下关键步骤： 1. 确定相邻杆件的相对坐标系：每个杆件相对于前一个关节的坐标系有一个新的Z轴（Zn-1）和X轴（Xn-1），其中Z轴通常定义为旋转轴，X轴垂直于两连杆的公共垂线。 2. 参数确定：包括连杆长度ln（从Zn-1到Zn沿Xn-1的距离）、两关节轴之间的扭角αn（Zn-1到Zn绕Xn的旋转角）、偏置距离dn（Xn-1到Xn沿Zn-1的垂直距离）以及两连杆间的角度θn（Xn-1到Xn绕Zn-1的旋转角）。 3. 右手定则的应用：用于确定Y轴的方向，确保坐标系符合右手坐标系统的规则。 在实际的机器人结构中，关节可以分为转动关节和移动关节。转动关节提供一个旋转自由度，如铰链，而移动关节提供一个平移自由度。每个关节都连接着两个杆件，确保了机器人结构的稳定性和运动传递。对于多关节机器人，特别是工业机器人，通常会有多个这样的关节和杆件组合，以实现复杂的空间运动。 本资源详细阐述了两种常见的杆件构形： 1. 两个平行的转动关节，无扭转：在这种情况下，连杆的长度ln是重要的参数，且关节间的夹角θn是可变的，可以绕Zn-1轴旋转。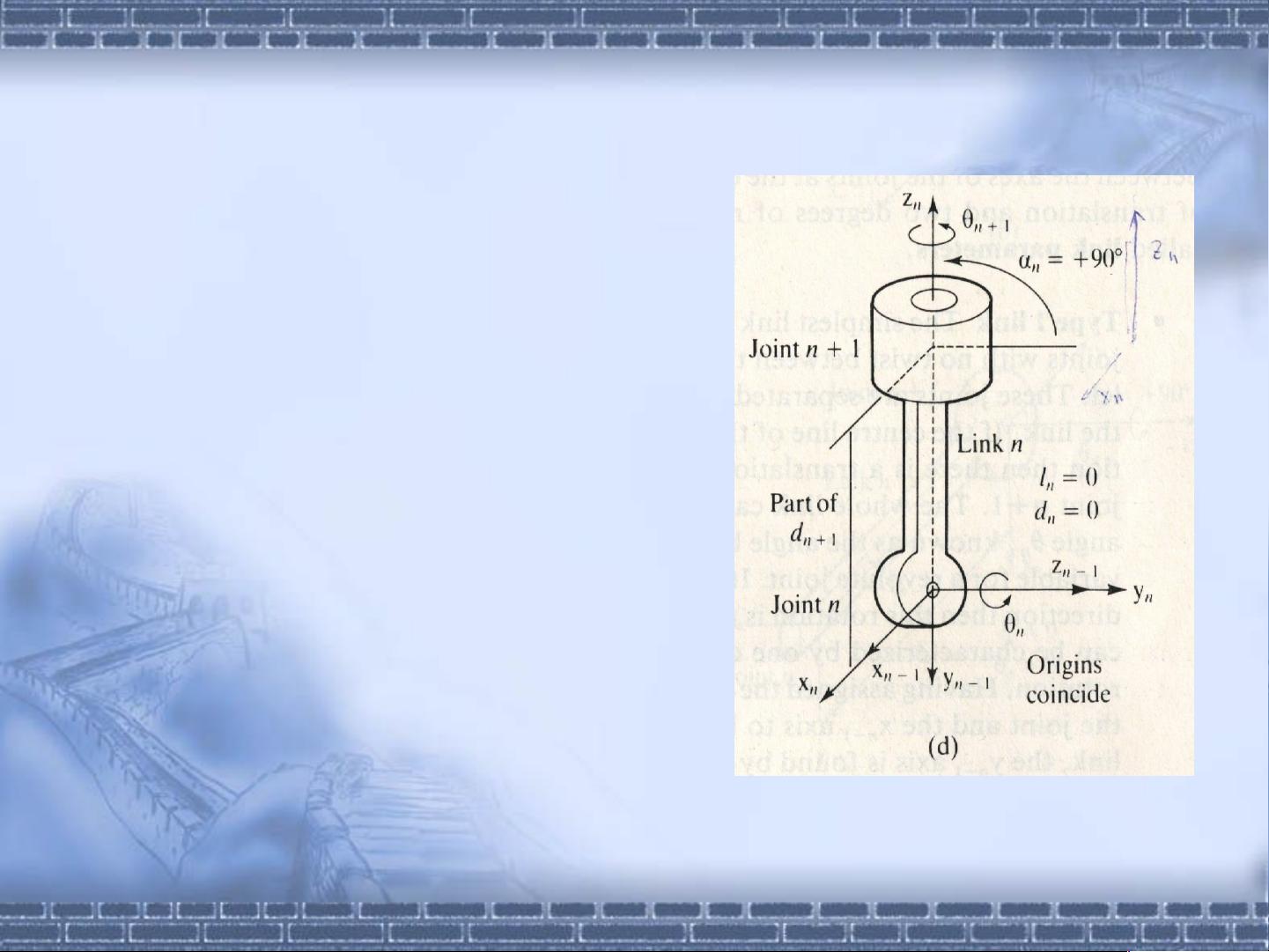 2. 两个形成90°扭转的转动关节：这种情况涉及到一个空间旋转，连杆长度ln同样重要，且关节间的相对扭转和角度变化需要特殊考虑。 通过理解DH坐标系的建立方法和参数，可以有效地进行机器人运动学分析，这对于机器人控制系统的设计和路径规划至关重要。