均值漂移算法Mean-Shift详解与应用

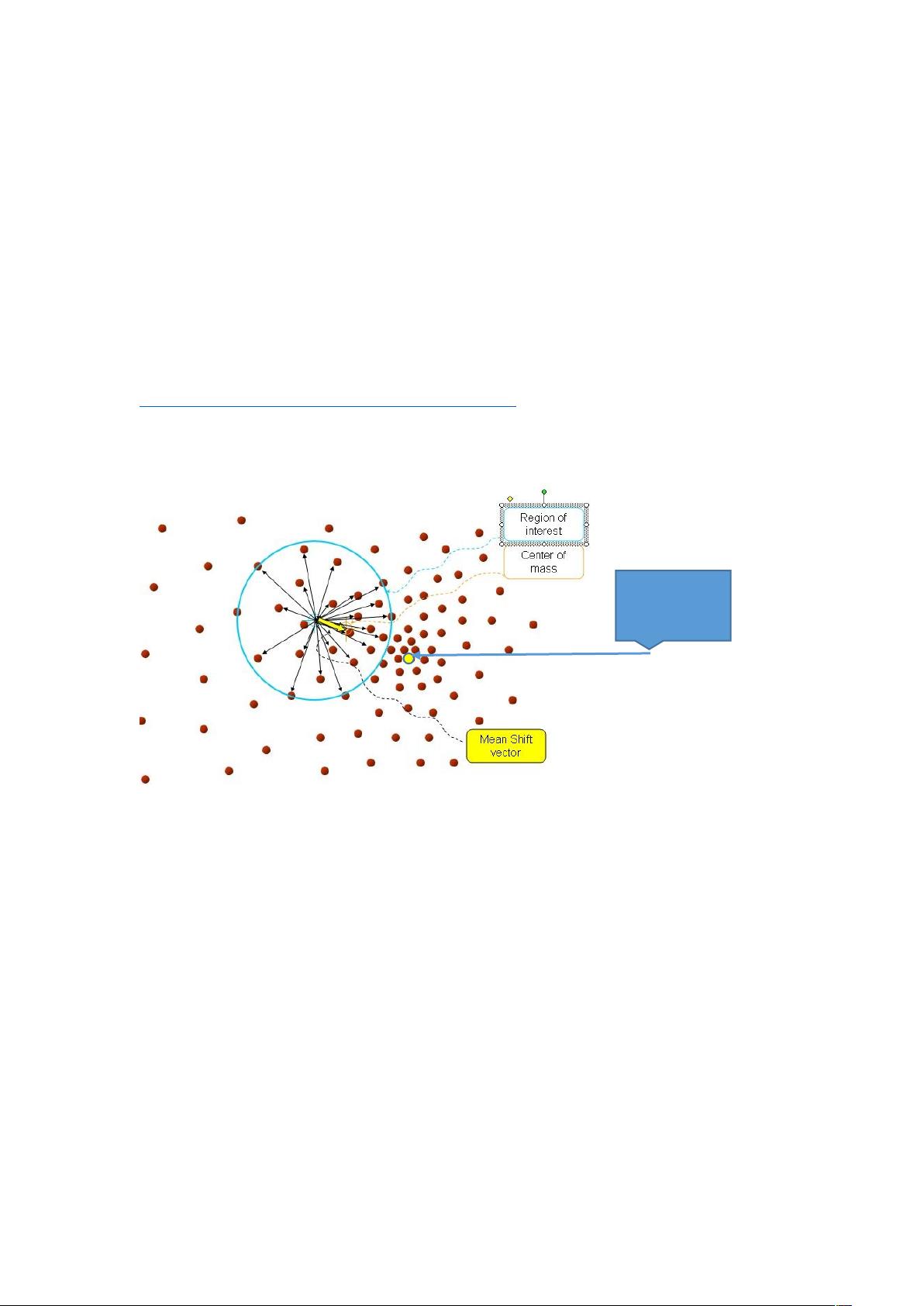
"这篇资源是关于meanshift算法的个人总结，包括了算法的基本概念、发展历史、应用以及算法的推导。文中提到了meanShift算法的起源和在追踪领域的应用，以及如何通过迭代过程找到数据的密度峰值。" Meanshift算法是一种无参数的聚类和追踪方法，它通过不断迭代寻找数据分布的局部峰值或高密度区域。最初由Fukunaga在1975年提出，早期仅是一个简单的统计概念，随着时间推移，其内涵得到了丰富和发展。 在Yizong Cheng于1995年的论文中，meanShift算法引入了核函数的概念，这意味着不同距离的样本点对均值偏移的贡献可以有所不同。此外，通过设定权重系数，可以考虑不同样本点的重要性，从而增强了算法的适应性和灵活性。这项改进使得meanShift算法在图像处理、物体追踪等领域得到了广泛应用，尤其是在实时追踪中表现突出。 Mean-shift算法的核心思想是一个向量从当前点移动到其周围数据点的加权平均位置，这个过程称为“向重心偏移”。算法通过反复迭代这一过程，最终会收敛到概率密度最高的区域，即数据的局部峰值。这个特性使得meanShift特别适合用于寻找数据集中的模式或集群。 算法的推导过程中，初始的偏移向量计算涉及到一个半径为h的高维球区域内的所有点。然而，原始公式中所有点的权重相等，这并不符合实际情况，因为靠近当前点的样本应具有更大的影响力。因此，引入了核函数，如高斯核，来解决这个问题。核函数能够根据样本点与当前点的距离给予不同的权重，距离越近的点权重越大，从而更准确地反映出数据的局部结构。 meanShift算法是一种强大的工具，尤其在处理高维数据和需要寻找密集区域的问题时。其优势在于无需预先确定簇的数量，且能自动适应数据的分布。尽管如此，算法的效率和准确性可能受到选择的窗口大小（h）和核函数类型的影响，需要根据具体问题进行调整。通过理解算法的原理和优化策略，我们可以更好地应用meanShift解决实际问题。