二维金属体散射计算：矩量法MATLAB实现

"该文档是关于使用矩量法计算二维金属体散射的MATLAB程序实现，主要涉及电磁波与金属圆柱体、椭圆柱体的交互计算。" 基于矩量法的二维金属体散射计算是电磁学领域的一个重要问题，特别是在天线与微波工程中广泛应用。这种方法用于分析物体对电磁波的散射行为，通常用于设计和优化雷达系统、无线通信设备等。本文档详细介绍了如何运用矩量法（Method of Moments, MoM）来解决这一问题，并提供了一个MATLAB程序实现。 1. 问题描述： 问题设定为计算一个二维金属圆柱体和椭圆柱体的散射场，入射波被简化为垂直于z轴的TM或TE平面波。在这种情况下，研究的是物体对垂直入射电磁波的响应。 2. 矩量法求解过程： 2.1 电场积分方程： 首先，通过麦克斯韦方程组建立电场积分方程。方程(3)表示在圆柱表面上的面电流产生的总场。利用金属表面的边界条件（即电场在金属表面为零），可以推导出关于面电流的方程。接着，将散射体截面离散化，采用点匹配法将积分方程转换为代数方程组。 2.1.2 离散化： 选择特定的基函数，如式(6)所示，将连续的积分方程转化为离散形式，得到矩阵方程(P){J}={b}。这里的P矩阵、L矩阵和U矩阵是用于求解的矩阵，J表示面电流分布。 2.1.3 方程组求解： 通过LU分解，可以有效地求解矩阵方程，从而得到面电流J。进而，可以计算散射场E_s和散射截面Scattering Cross Section (SCS)。 2.1.4 结果验证： 通过模式展开法（如格林函数方法）的结果与矩量法求解的结果进行比较，以验证计算的准确性。 2.2 磁场积分方程： 对于TE波入射的情况，仅考虑磁场的横向分量，建立磁场积分方程。同样地，离散化处理并求解，得到相应的面电流分布和散射特性。 3. 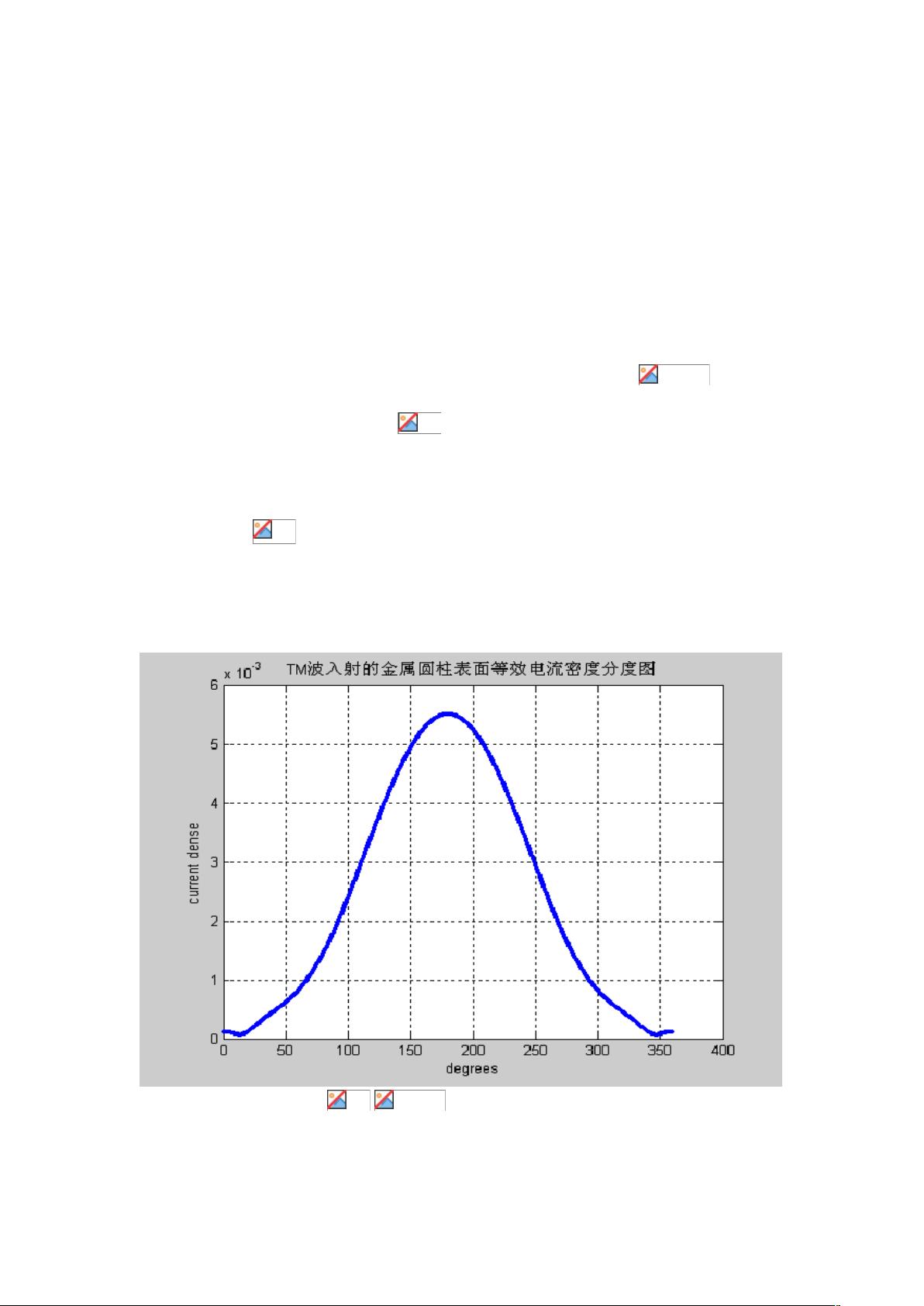计算机数值实验及分析： 这部分未给出具体细节，但可以理解为使用MATLAB程序进行了实际的计算和模拟，可能包括不同参数的测试、散射特性的可视化以及与理论值的比较。 这个MATLAB程序为研究者提供了计算二维金属体散射的强大工具，可以帮助理解和优化电磁波与物体的相互作用。通过调整输入参数，可以研究不同形状、尺寸和材质的物体对电磁波散射的影响，从而在工程应用中找到最佳设计。