计算机几何基础算法详解：从矢量到圆内包含判定

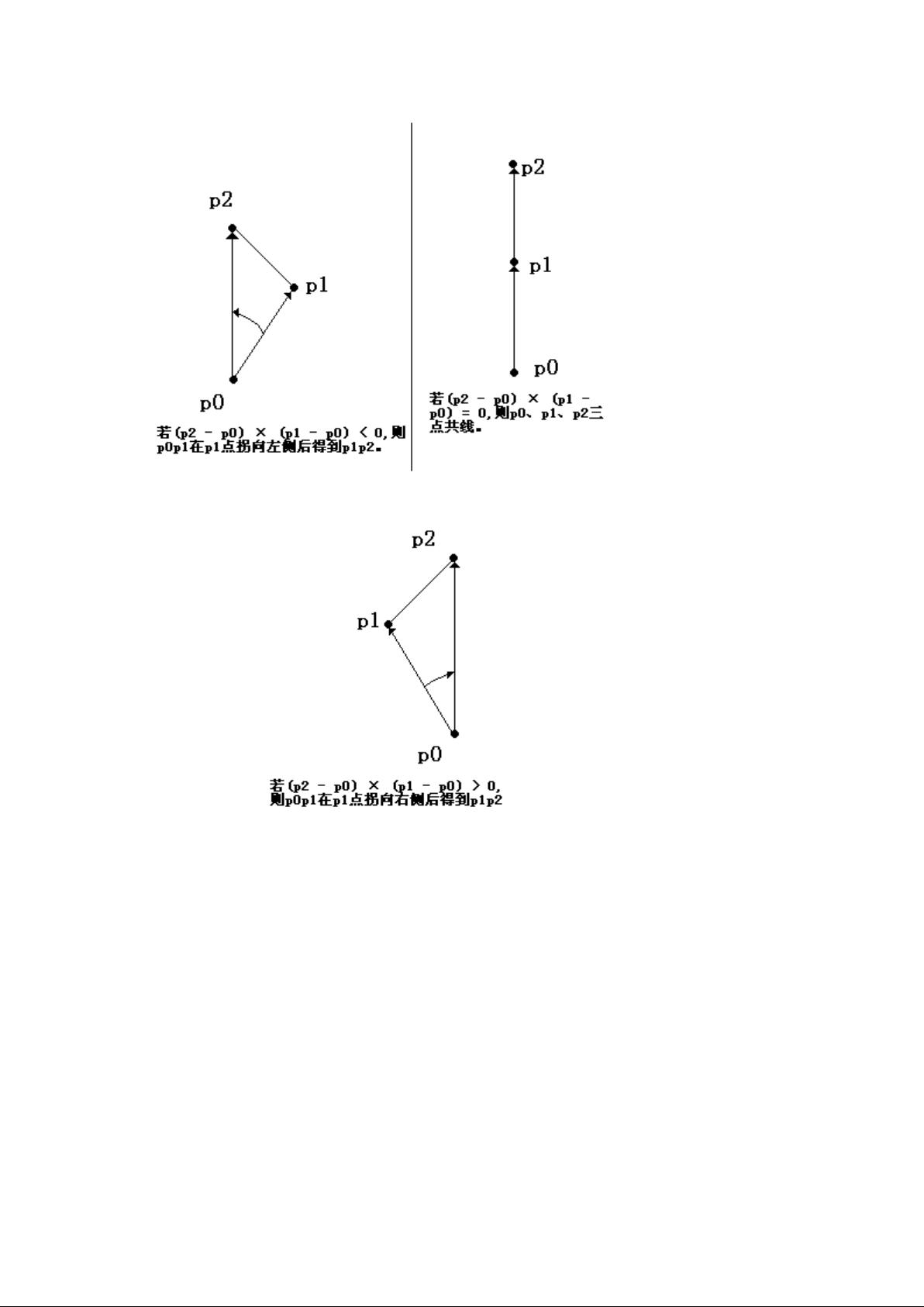
本文主要介绍了图形学中最常用的几个算法，这些算法在计算几何领域发挥着关键作用。计算几何是计算机科学的一个分支，专注于设计和分析处理几何问题的高效算法，广泛应用于图形学、机器人技术、超大规模集成电路设计和统计等领域。 文章首先阐述了矢量的概念，指出有向线段是具有起点和终点有序的线段，当起点在原点时，它被表示为矢量。矢量加减法和矢量叉积是基础操作，其中矢量叉积用于计算两个矢量形成的平行四边形的面积，其结果是一个标量，且有交换律和反对称律的特性。通过叉积的符号，可以判断两个矢量的相对位置，如顺时针还是逆时针。 接下来，文章列举了一系列几何问题的判断算法，如点与线段、线段与线段、线段与多边形、矩形与点、矩形与其他几何形状的包含关系，以及判断圆与几何形状的关系。这些问题涉及到空间定位、形状判定和边界检测，是实现图形交互和场景分析的基础。 此外，文中还提及了求解特定距离和交点的算法，例如计算点到线段、折线、矩形、多边形以及圆的最近距离和对应的交点坐标。这些算法对于碰撞检测、路径规划等场景至关重要。 最后，文章提到了凸包的概念，它是所有点集合中最小的凸多边形，用于概括一个形状的外部轮廓。求凸包的方法也是计算几何中的核心内容，这对于形状简化和区域划分等问题处理非常有用。 本文全面地介绍了计算几何中的基本概念和实用算法，为理解和应用这些算法于实际问题提供了清晰的指导。掌握这些算法对于从事图形学、游戏开发、CAD软件或相关领域的专业人士来说，是一项必备技能。