MATLAB实现PCA算法详解：数据降维关键步骤与验证

本文主要介绍了在MATLAB中实现数据降维技术——主成分分析（PCA）的方法。PCA是一种统计学上的数据预处理技术，其核心思想是通过线性变换将原始特征转换为一组新的、不相关的特征，这些新特征又被称为主成分，它们按顺序解释了原始数据中最大的方差。在MATLAB中，可以使用内置的`pca`函数来执行PCA，该函数包括以下几个关键步骤： 1. **数据预处理**：首先对输入数据进行标准化处理，确保各个特征具有相同的尺度。在MATLAB的`pca`函数中，`ingredients`数据集被加载并标准化。 2. **PCA计算**： - **协方差矩阵**：通过计算标准化后的矩阵的协方差矩阵，这是PCA的核心步骤，用于确定各个特征之间的相关性。 - **特征值和特征向量**：计算协方差矩阵的特征值和对应的特征向量，特征值大小反映了特征的重要性，特征向量则是数据在主成分空间中的方向。 - **降维选择**：基于特征值，通常选择贡献率较大的前几个主成分，如文中提到的前两个主成分就能解释数据的97%以上信息。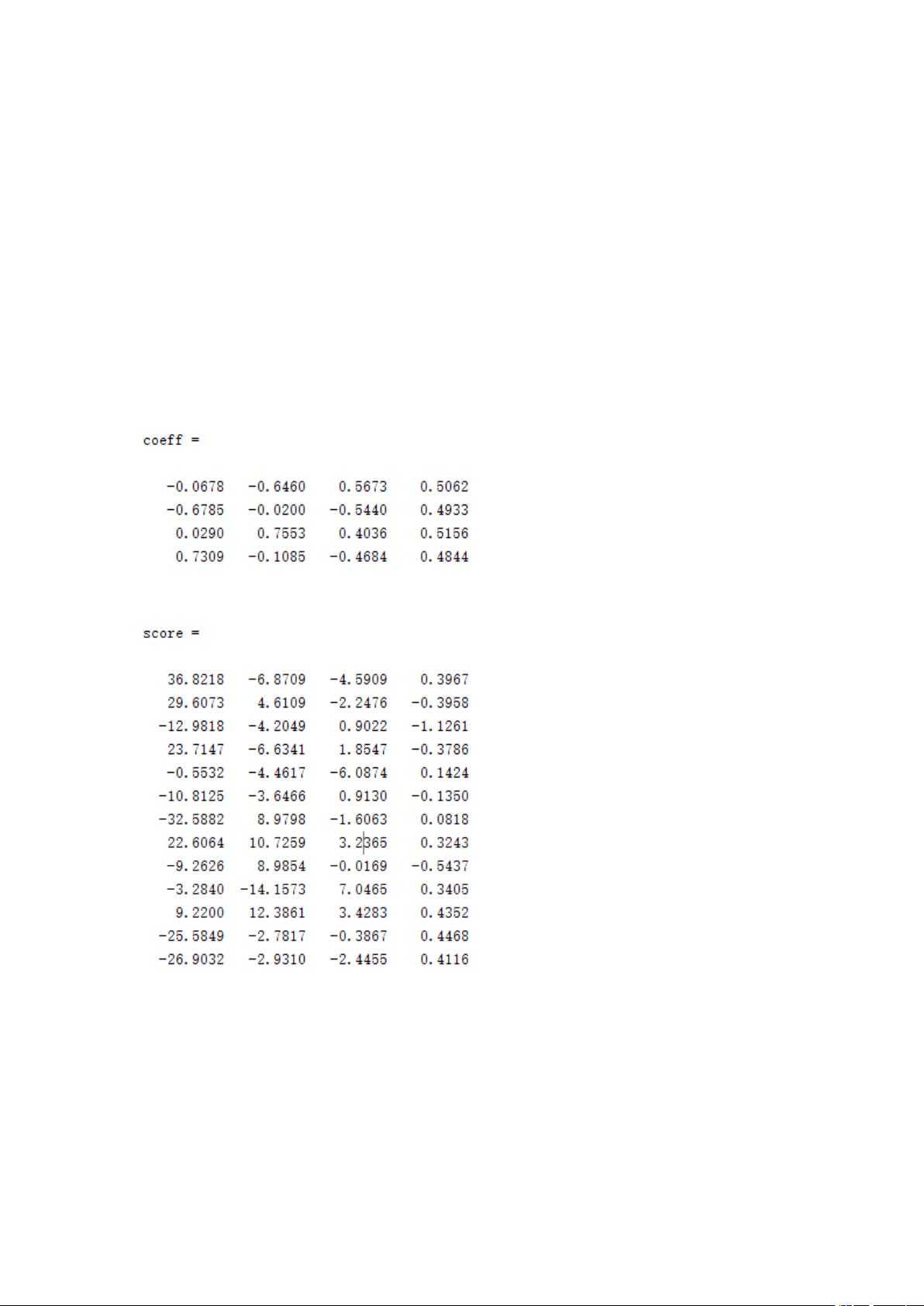 - **`pca`函数应用**：`coeff`表示特征向量（即主成分系数），`score`是标准化数据投影到主成分上的得分，`latent`是特征值（即主成分方差），`tsquared`是Hotelling's T-Squared Statistic，衡量数据点与均值的距离。 3. **验证与自定义实现**： - 通过`pca`函数直接得到的结果与手动计算的特征值、特征向量和得分匹配，但需要注意结果的唯一性取决于数据的标准化方式。 - 自定义实现时，需要对特征值进行排序，可能需要使用`fliplr`函数进行矩阵翻转，以确保特征向量的方向与`coeff`一致。在实际操作中，发现第二主成分与`coeff`中对应成分值相反，这在高维度数据中可能更明显。 4. **目标结果提取**：PCA的主要目标是保留关键信息，因此最后保留的是`score`矩阵的前几列，即主成分得分，用于重构或进一步分析。 通过以上步骤，作者不仅演示了如何使用MATLAB的内置`pca`函数，还提供了自定义实现PCA的实践经验，帮助读者理解PCA背后的计算原理和MATLAB中的实际应用。在实际项目中，PCA常用于数据可视化、特征选择、异常检测等领域，以减少数据复杂性，提高模型效率。