基于MMSE的并行干扰取消ASIC实现MIMO软输入软输出检测
需积分: 9 75 浏览量
更新于2024-09-11
收藏 1.75MB PDF 举报
"这篇论文是关于ASIC实现软输入软输出（Soft-Input Soft-Output, SISO）MIMO检测器的，使用了基于最小均方误差（Minimum Mean-Squared Error, MMSE）的并行干扰取消（Parallel Interference Cancellation, PIC）技术。该工作在无线通信系统中具有重要意义，特别是对于满足现代无线通信系统如IEEE 802.11n和3GPP-LTE的数据速率和链路可靠性需求。MIMO技术是这些系统的关键，但要充分利用其潜力，需要依赖迭代MIMO解码和SISO数据检测。
作者Christoph Studer、Schekeb Fateh和Dominik Seethaler提出了一种低复杂度的MMSE算法，设计了相应的VLSI架构，并实现了一个四流1.5平方毫米的检测芯片，采用90纳米CMOS工艺制造。该ASIC芯片包含了所有必要的预处理电路，并且在峰值数据速率上超过了600Mb/s，符合IEEE 802.11n标准。此外，论文还与当前最先进的MIMO检测器进行了比较，展示了其性能优势。
MIMO技术在多输入多输出无线通信系统中通过利用空间多样性实现了更高的频谱效率和抗干扰能力。SISO检测器在这种系统中扮演关键角色，因为它能够提供软信息，即对每个符号概率的估计，这对于迭代解码至关重要。而MMSE算法则是在这种检测中降低误码率的一种有效方法，它通过最小化预测误差的均方值来估计信号。
并行干扰取消是一种有效的干扰抑制策略，它在多个接收天线之间并行地执行干扰消除，从而提高信号恢复的准确性和系统的整体性能。这种技术在多用户环境中尤其有用，可以减少不同用户间的数据流相互干扰。
ASIC（应用特定集成电路）实现的优势在于它可以针对特定任务优化硬件，从而实现高效、低功耗的运算。论文中的ASIC设计不仅实现了高性能，还考虑了面积效率，使得四流MIMO检测器能在1.5mm²的芯片面积内实现，这是在90纳米工艺技术下对体积和功耗的有效控制。
这篇论文为迭代MIMO解码提供了一种实际可行的硬件解决方案，有助于推动无线通信系统的发展，特别是在高数据速率和低延迟要求的应用中。通过创新的MMSE PIC算法和ASIC设计，该工作为实现更高效、更可靠的MIMO系统奠定了基础。"
STUDER, FATEH, AND SEETHALER 3
I=1
I=1
I=2
I=2
I=4
I=8
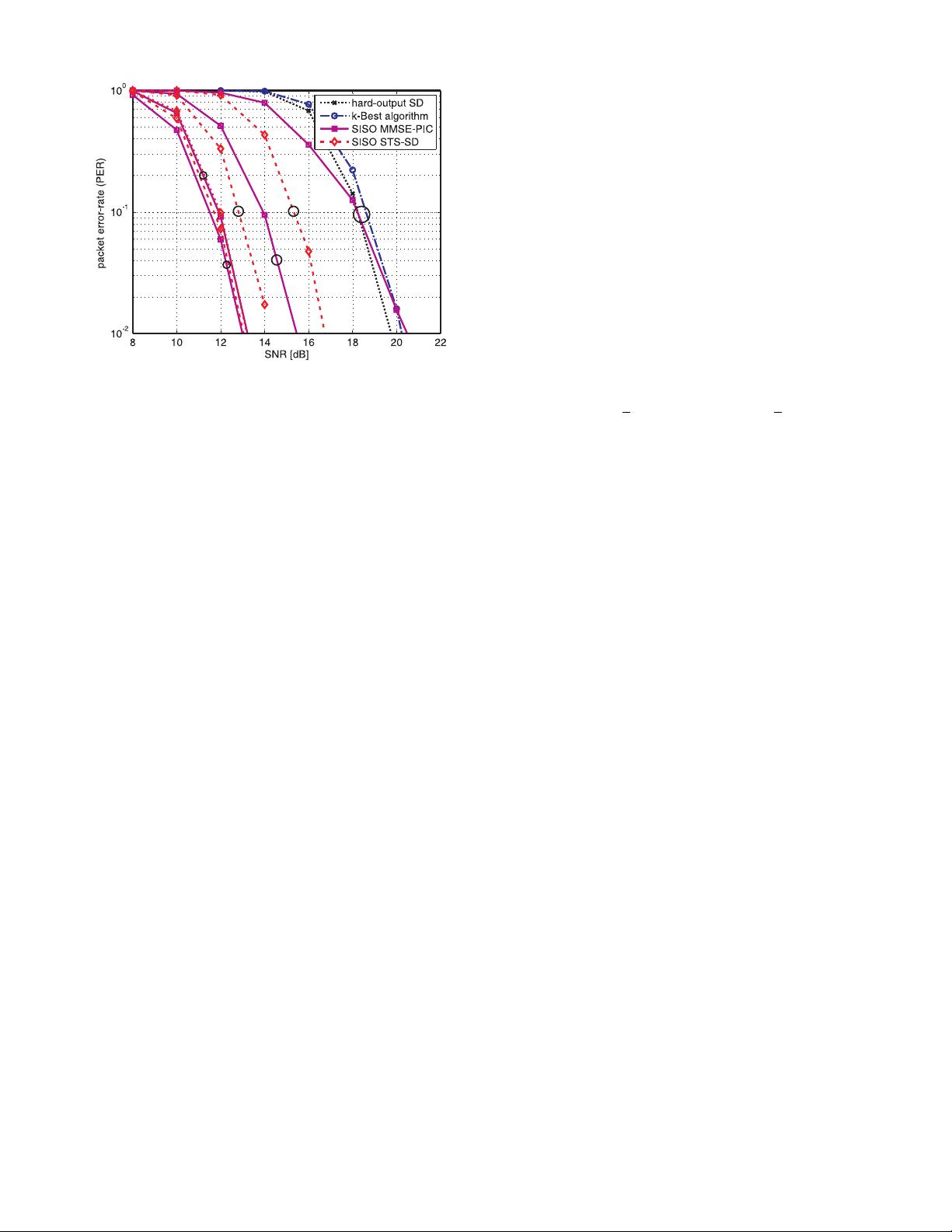
Fig. 2. PER versus SNR performance of a coded MIMO system using various
iterative (using I ∈ {2, 4, 8} number of iterations) and non-interative (I = 1)
MIMO detection algorithms.
enables to achieve 10% PER at 12 dB SNR for both SISO
STS-SD and SISO MMSE-PIC, compared to the more than
18 dB SNR that is required by hard-output SD and the k-Best
algorithm. Hence, four iterations improve the performance by
more than 6 dB SNR at IEEE 802.11n-relevant PERs. Note
that the SNR-performance gain from four to eight iterations
is only 0.25 dB, which indicates that performing more than
four iterations does not pay off in practical systems. We
emphasize that the SNR-performance advantage of iterative
MIMO decoding ultimately leads to an increased system
throughput (as higher data-rates can be used reliably at the
same SNR), better coverage, and improved range (since the
lowest data-rate can be decoded reliably at lower SNR).
We finally note that SISO STS-SD outperforms SISO
MMSE-PIC for a small number of iterations. However, the
SISO STS-SD algorithm requires i) roughly 8× higher compu-
tational complexity than SISO MMSE-PIC (cf. Section V-C3)
and ii) SD-based algorithms exhibit—in contrast to the other
considered algorithms—a non-constant throughput strongly
depending on the SNR and the channel realization. Since
practical MIMO receivers need to cope with varying channel
conditions and transmission rates, the non-constant throughput
renders implementations of SD extremely difficult (see [7] for
a corresponding discussion). Both drawbacks associated with
SD finally led to our decision to favor the SISO MMSE-PIC
algorithm for implementation.
C. SISO MMSE-PIC Algorithm
Even for a small number of spatial streams (say M
T
> 2),
exact computation of the LLRs in (1) entails prohibitively
high computational complexity. Therefore, a variety of sub-
optimum algorithms has been proposed in the literature,
e.g., [13], [15]. In this paper, we focus on the SISO MMSE-
PIC algorithm initially proposed by Wang and Poor in
1999 [15] in the context of multi-user detection. Since then,
various algorithm optimizations have been proposed [21]–[24].
The following five paragraphs summarize the SISO MMSE-
PIC algorithm as described in [23].
1) Computation of Soft-Symbols: The algorithm starts by
computing estimates ˆs
i
for i = 1, . . . , M
T
(referred to as “soft-
symbols”) for the transmitted symbols s
i
according to [21]
ˆs
i
= E[s
i
] =
X
a∈O
P[s
i
= a] a (2)
where P[s
i
= a] =
Q
Q
b=1
P[x
i,b
= k] denotes to the a-priori
probability of the symbol a ∈ O with k = [a]
b
referring to the
bth bit associated with the symbol a. The reliability of each
soft-symbol ˆs
i
is characterized by its variance
E
i
= Var[s
i
] = E
h
|e
i
|
2
i
(3)
with e
i
= s
i
− ˆs
i
. The a-priori probabilities involved in the
computation of the soft-symbols (2) and their variances (3)
are calculated on the basis of the a-priori LLRs L
A
i,b
delivered
by the channel decoder.
3
According to [25], we have
P[x
i,b
= k] =
1
2
1 + (2k − 1) tanh
1
2
L
A
i,b
(4)
which can be approximated efficiently in hardware through
table look-ups.
As observed in [23], using intrinsic a-priori LLRs in the
computation of (4) instead of the extrinsic ones leads, in gen-
eral, to significantly better error-rate performance of the SISO
MMSE-PIC algorithm. We therefore exclusively use intrinsic
a-priori LLRs for the computation of (4) throughout the pa-
per. We finally note that for most Gray mappings (including
that used in IEEE 802.11n) the soft-symbols in (2) and their
corresponding variances in (3) can be computed efficiently in
hardware using the method proposed in [24].
2) Parallel Interference Cancellation (PIC): With the aid
of the previously computed soft-symbols (2), the algorithm
considers each of the i streams separately and cancels the
interference in y induced by all other streams j 6= i as follows:
ˆ
y
i
= y −
X
j,j6=i
h
j
ˆs
j
= h
i
s
i
+
˜
n
i
(5)
where
˜
n
i
=
P
j,j6=i
h
j
e
j
+ n corresponds to the remaining
noise-plus-interference (NPI).
3) MMSE Filter-Vector Computation: In order to reduce
the NPI in each
ˆ
y
i
of (5), a linear MMSE filter is used. These
M
T
MMSE filter vectors are computed according to [21]
˜
w
H
i
= E
s
h
H
i
e
A
−1
i
(6)
where
e
A
i
= H
e
Λ
i
H
H
+ N
0
I
M
R
(7)
and
e
Λ
i
being an M
T
× M
T
diagonal matrix having entries
˜
Λ
j,j
=
(
E
j
, j 6= i
E
s
, j = i.
It is important to realize that (6) requires the inversion of a
M
R
× M
R
-dimensional matrix for each of the M
T
streams,
for each received vector, and for each iteration, which in-
hibits an efficient implementation in hardware. In order to
substantially reduce this computational burden, a novel low-
complexity method is proposed in Section III.
3
The LLRs are initialized as L
A
i,b
= 0, ∀i, b, in the first iteration.
剩余11页未读，继续阅读
点击了解资源详情
点击了解资源详情
点击了解资源详情
2008-11-19 上传
2021-05-27 上传
2017-12-02 上传
2021-03-20 上传
2021-05-23 上传
2021-10-03 上传
magiccarpet1
- 粉丝: 0
- 资源: 1
我的内容管理
展开
最新资源
- C语言数组操作：高度检查器编程实践
- 基于Swift开发的嘉定单车LBS iOS应用项目解析
- 钗头凤声乐表演的二度创作分析报告
- 分布式数据库特训营全套教程资料
- JavaScript开发者Robert Bindar的博客平台
- MATLAB投影寻踪代码教程及文件解压缩指南
- HTML5拖放实现的RPSLS游戏教程
- HT://Dig引擎接口，Ampoliros开源模块应用
- 全面探测服务器性能与PHP环境的iprober PHP探针v0.024
- 新版提醒应用v2：基于MongoDB的数据存储
- 《我的世界》东方大陆1.12.2材质包深度体验
- Hypercore Promisifier: JavaScript中的回调转换为Promise包装器
- 探索开源项目Artifice：Slyme脚本与技巧游戏
- Matlab机器人学习代码解析与笔记分享
- 查尔默斯大学计算物理作业HP2解析
- GitHub问题管理新工具：GIRA-crx插件介绍
