离散时间控制系统与采样控制

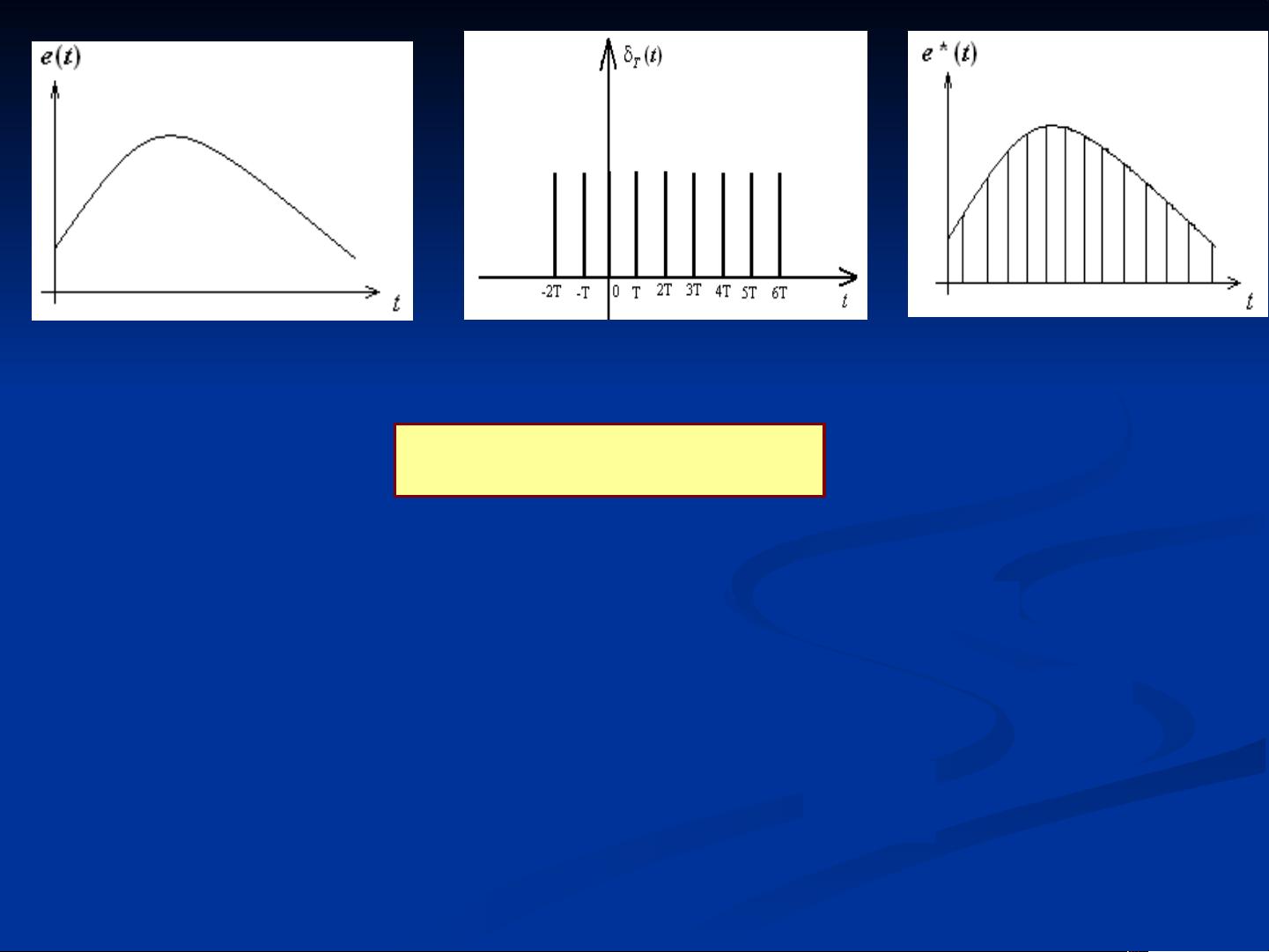
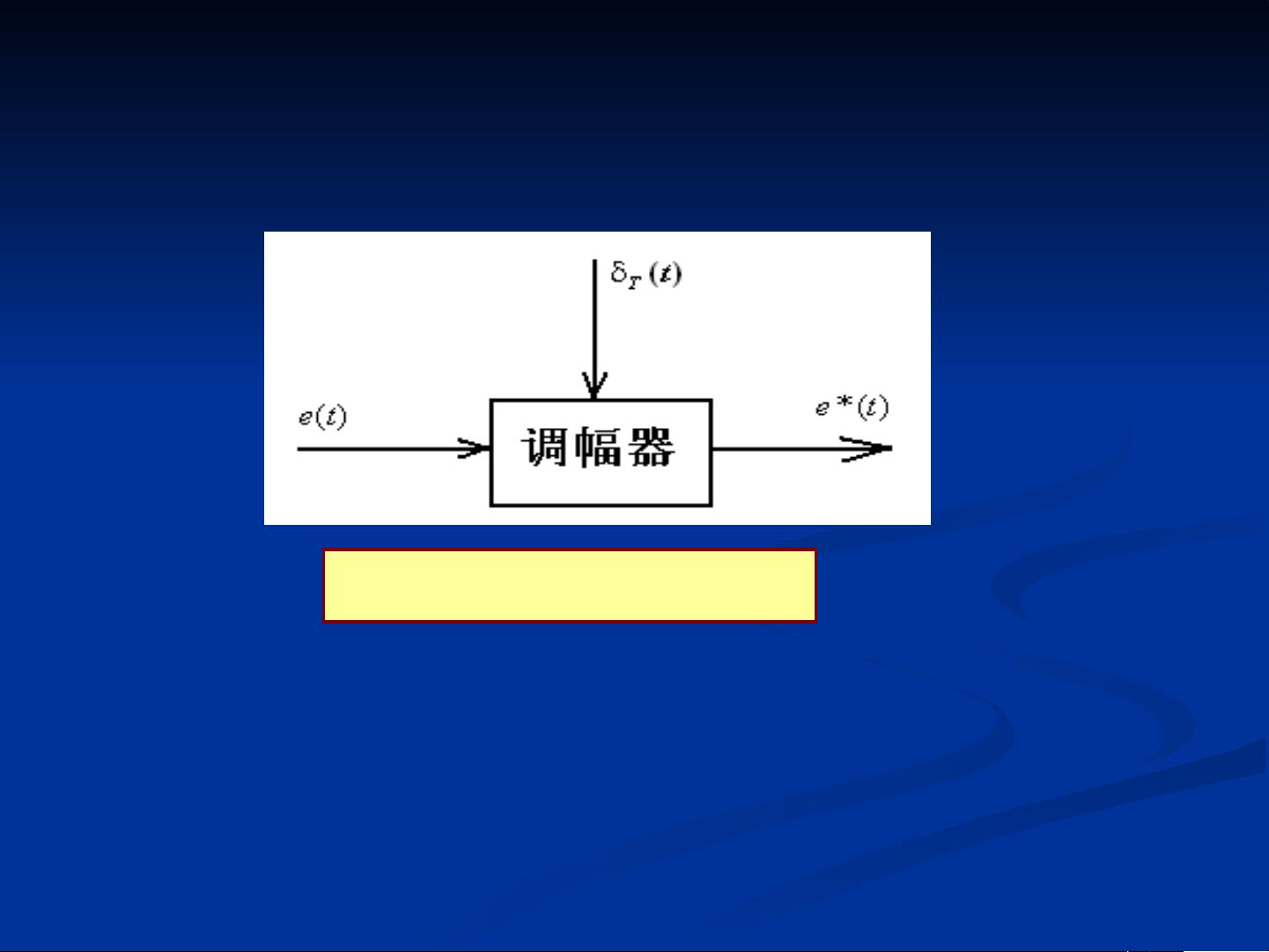
"第8章采样控制系统" 在控制系统领域，采样控制系统占据着重要的地位，它们与连续时间控制系统并存，但处理方式有所不同。本章深入探讨了采样控制系统的各个方面，包括分析方法、数学描述以及性能分析。下面将详细阐述这些关键知识点。 首先，连续时间控制系统是基于时间连续函数的系统，信号在整个系统中不间断地变化。相反，离散时间控制系统，即采样控制系统，其信号在时间上是离散的，由一系列脉冲序列或数字信号组成。这包括了采样数据信号和数字信号，例如在过程控制系统（PCS）中常见的形式。 离散控制系统是更广泛的类别，它不仅包含采样控制系统，还涉及数字控制系统。在离散控制系统中，处理的对象是离散信号，可以是采样后的模拟信号或者是纯数字信号。而采样控制系统则特指那些涉及到采样和保持操作的系统，它们通常包含A/D（模数转换器）和D/A（数模转换器）部件，用于在连续和离散世界之间转换信号。 数字控制系统则进一步限制，信号处理完全在数字域内完成，如数字仿真系统。这里的输入和输出都是数字序列。例如，当一个计算机控制系统（如图8-1所示）接收到模拟输入时，A/D转换器会将其转化为数字信号，然后计算机依据预设的控制算法进行计算。计算结果通过D/A转换器转换回模拟信号，以驱动实际的被控对象。 Z变换理论是分析离散时间系统的重要工具，它在数学模型的离散化过程中起着关键作用。Z变换允许我们将离散时间信号转换到Z域，从而可以应用类似于连续时间系统分析的方法。脉冲传递函数是另一个关键概念，它描述了离散系统对输入信号的响应。 性能分析是采样控制系统研究的核心部分。稳定性是首要考虑的因素，确保系统在各种条件下都能稳定运行。稳态特性关注系统在长期运行后达到的平衡状态，而动态特性则涉及系统响应输入信号的速度和形状。这些特性可以通过数学工具如奈奎斯特稳定判据、根轨迹法等进行评估。 第8章深入讲解了采样控制系统的理论基础和实践应用，涵盖从采样和保持的数学描述，到离散化模型的建立，再到系统性能的全面分析。理解和掌握这些知识对于设计和优化现代工业自动化系统至关重要。