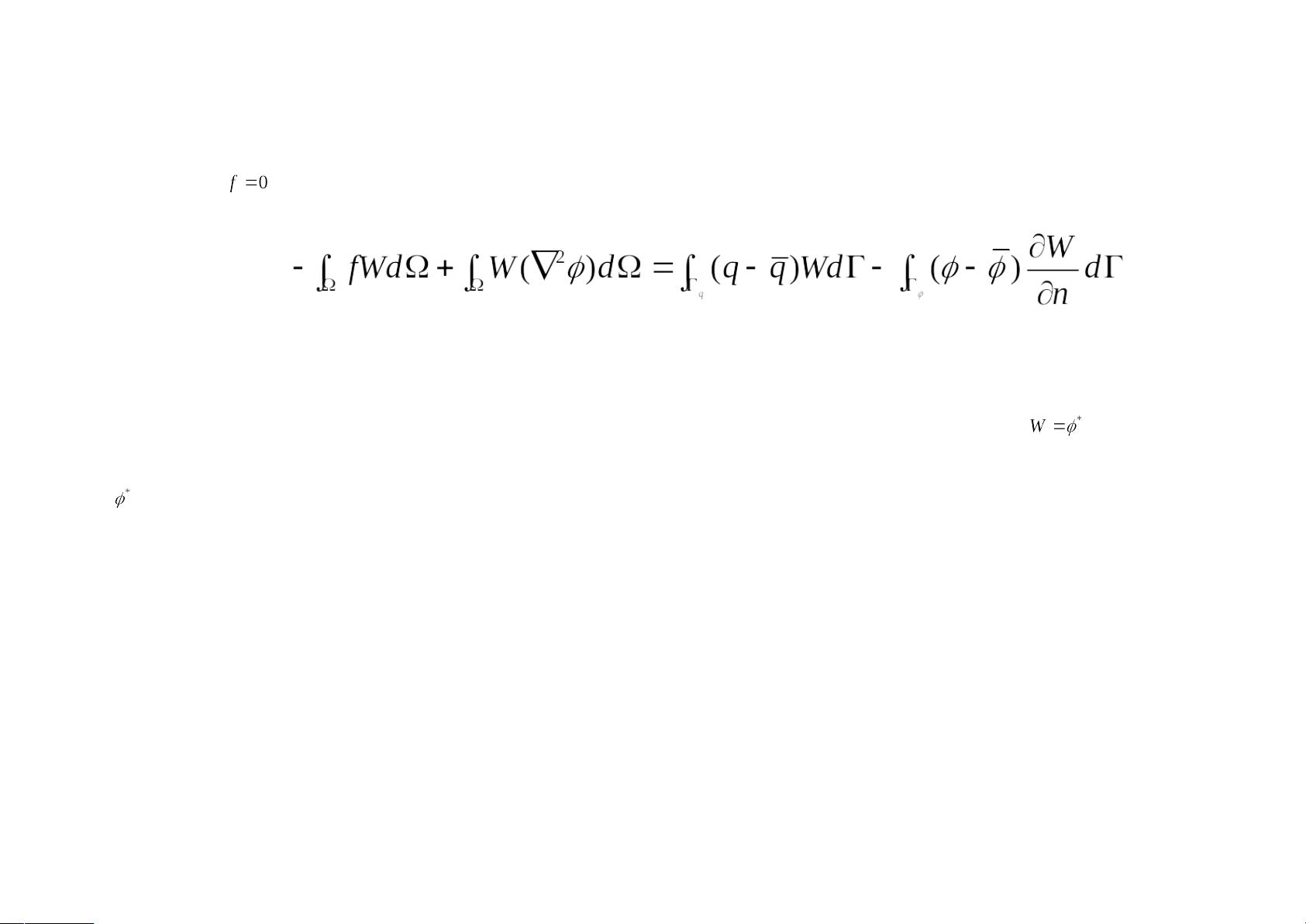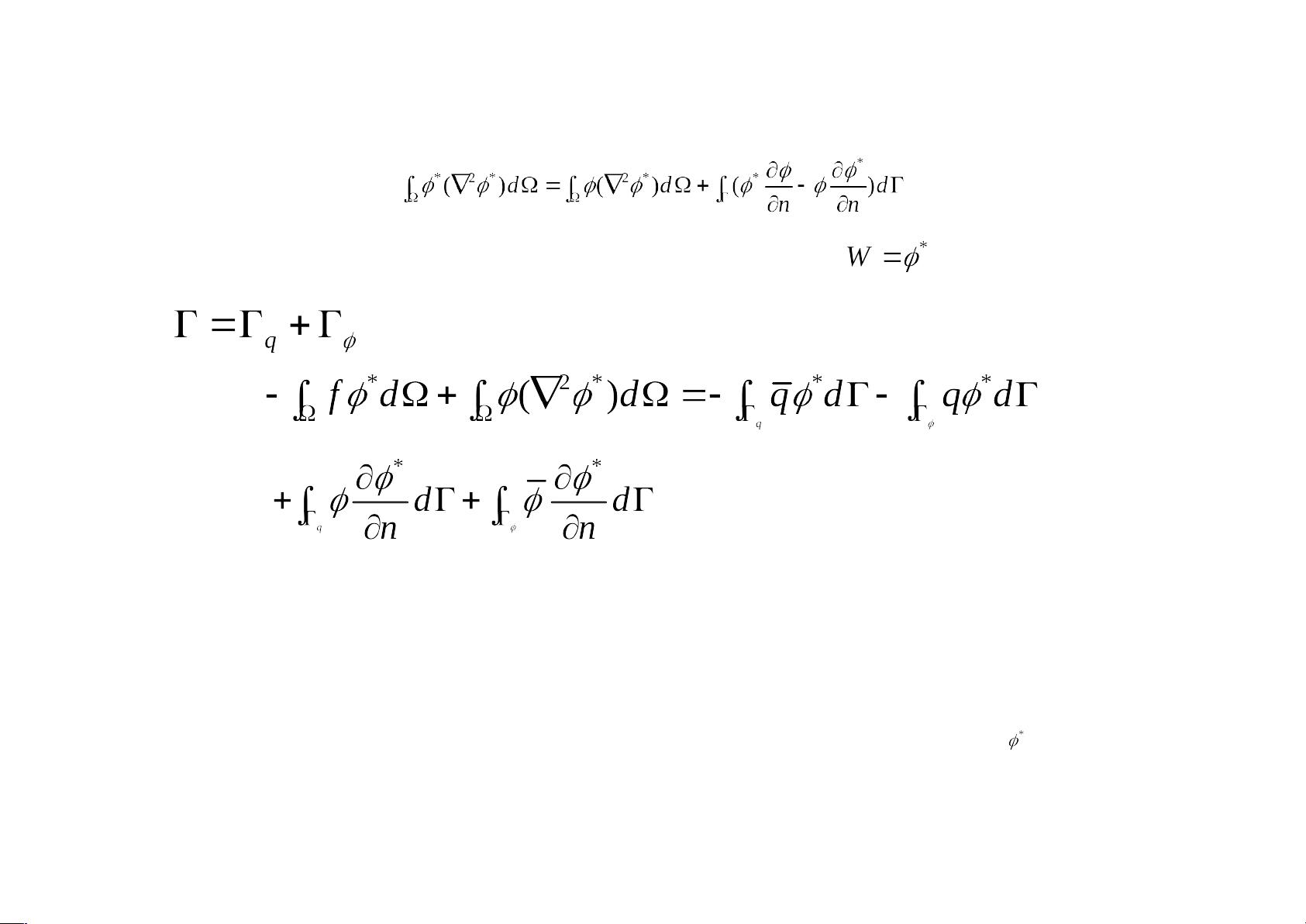边界元法详解与应用

"这篇文档详细介绍了边界元方法及其在各种工程问题中的应用，包括弹性力学、断裂力学等领域。文中特别提到了直接法和间接法，其中直接法使用物理意义明确的变量来建立积分方程，而间接法则使用可能含义不明确的变量。此外，文档还讨论了边界元法的优缺点，如降低问题维度、减少输入数据和提高计算精度，以及矩阵系数非对称的特性。最后，通过泊松方程的例子展示了边界单元法的具体应用。" 边界元方法，或称边界单元法（BEM），是七十年代发展起来的一种数值计算技术，主要用于解决物理、工程领域的各种问题，如弹性力学、断裂力学、流体力学等。该方法的核心在于将问题的求解集中在边界上，将广义位移和广义力作为独立变量，并利用满足场方程的奇异函数（源函数）作为加权函数，形成一种特殊的加权余量法。 边界元法的优势在于它能够将三维问题简化为二维，二维问题简化为一维，大大减少了需要处理的数据量和计算时间。由于只需要对边界进行离散，因此离散误差仅来源于边界，提高了计算精度。同时，域内变量可以通过解析式直接求得，无需像有限元法那样对整个区域进行网格划分。 文档中提到了边界元法的两种主要类型：直接法和间接法。直接法中，未知函数直接对应于边界上的物理量；而在间接法中，积分方程的建立可能涉及物理意义不太明确的变量，如位势问题中的单层位势和双层位势。对于直接法，文档进一步探讨了泊松方程的边界单元法求解，以此为例说明积分方程的建立过程。 泊松方程是描述势函数φ满足的微分方程，通常出现在电势、温度分布等问题中。在边界元法的应用中，首先会建立积分方程，这个过程通常涉及加权余量法和基本解的概念。基本解是微分方程的特定非齐次解，尽管找到它的解析形式可能困难，但在许多情况下可以直接引用已知的数学结果。 边界元法的系数矩阵通常是非对称的，并且是非零系数的满秩矩阵，这源于边界点与所有边界单元的关联。在编写程序实现边界元法时，必须考虑到这一特性，以确保正确处理这类矩阵。 边界元方法是一种强大的工具，尤其适用于处理边界条件复杂的问题，它简化了问题的复杂性，提高了计算效率，并且在理论和实际工程应用中都有广泛的应用。