动态信道捕获优化：MU-MIMO系统中的用户调度策略

152 浏览量更新于2024-08-26 收藏 313KB PDF 举报

MU-MIMO（多用户多输入多输出）技术在现代无线通信系统中发挥着关键作用，但其性能受到一个重要挑战：即由于频繁的信道状态信息（CSI）获取导致的维度损失，这会增加系统的开销，可能导致系统效率降低。本文主要探讨了在MU-MIMO系统中如何有效地进行用户调度，以平衡CSI获取与系统效率之间的关系。首先，作者提出了一个基于 genie-aided optimization problem (GAP) 的理论框架。GAP的目标是在每一步的调度决策中最大化Lyapunov-drift，这个过程考虑了用户的队列信息以及信道的波动性。通过这种优化方法，系统可以动态地选择最合适的用户进行数据传输，以实现整体吞吐量的最大化。然而，尽管GAP规则理论上具有最优的吞吐量性能，但它在实践中由于实施复杂性和可能带来的公平性问题，实际应用上可能存在困难，因为频繁的 CSI 更新会导致额外的延迟和计算负担。为了克服这些问题，作者提出了两种实际可行的动态信道捕获策略： 1. T-Frame动态信道捕获方案：这种方法将信道捕获操作限制在特定的时间窗口（T-Frame）内，避免了不必要的CSI更新。通过设定合理的帧结构，基站可以在保证足够准确的CSI的同时，减少系统因频繁获取而产生的开销。这样既能控制延迟，又能保持一定的系统性能。 2. 功率-law Dynamic Channel Acquisition (DCA) 策略：这是一种基于功率控制的信道捕获策略，它根据当前信道条件和用户需求动态调整 CSI 获取的频率和强度。通过权衡不同用户之间的信噪比和所需的 CSI 更新频率，该策略旨在降低系统总体开销，同时尽可能减小服务差异，提高公平性。这篇研究论文深入探讨了MU-MIMO系统中动态信道捕获的重要性，并通过理论分析和实际方案设计，为解决CSI获取开销与系统性能之间的平衡问题提供了有价值的指导。实施这些策略有助于提升MU-MIMO系统的效率、延迟性能和公平性，从而推动无线通信技术的进一步发展。

4338 IEEE TRANSACTIONS ON COMMUNICAT IONS, VOL. 62, NO. 12, DECEMBER 2014

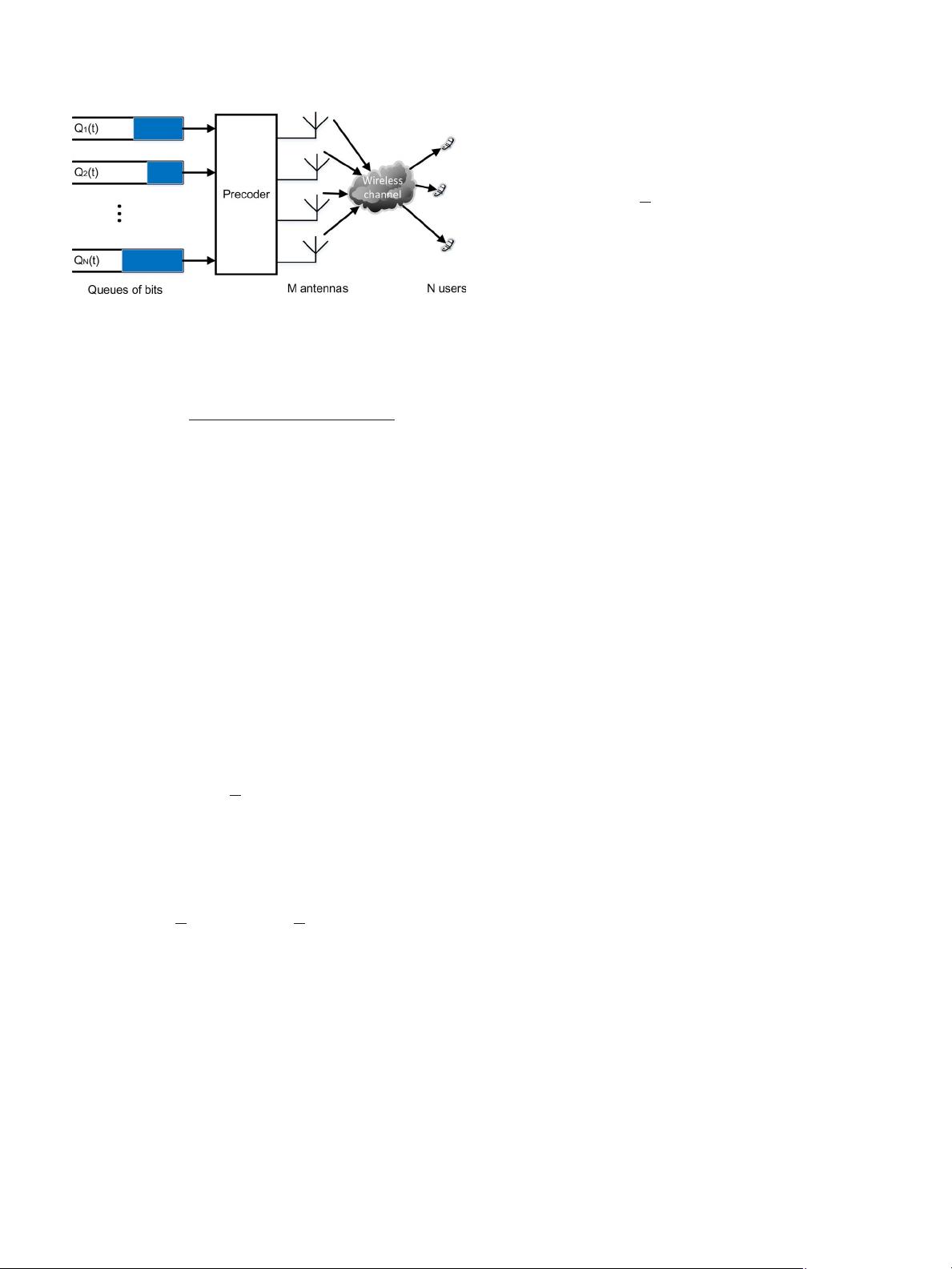
Fig. 2. System Model of a MU-MIMO Downlink Scenario.

matrix, and s(t) denotes the i.i.d. user data streams. The signal-

to-interference-noise ratio (SINR) of user-n is written as,

(t)=

ζ(t)



†

(t)w

(t)



∑

j=n

ζ(t)



†

(t)w

(t)



+ z

(t)

, (3)

where we write H(t)=[h

(t), h

(t),...,h

(t)]

†

and W (t)=

(t), w

(t),...,w

(t)], and n is the user index. Furthermore,

let Q

(t) denote the queue length in bits of user n at the begin-

ning of t-th channel use, let a

(t) denote the number of arrival

bits from upper layer to the physical layer between (t − 1)-th

and t-th channel uses, and let µ

(t) denote the allocated number

of service bits to Queue-n, which equals the allocated service

rate (bits/channel use) in this case. Then the queuing dynamics

are written as

(t + 1)=Q

(t) − ˜µ

(t)+a

(t), (4)

where ˜µ

(t)=min{Q

(t), µ

(t)} denotes the actual service

number of bits, considering the circumstances that sometimes

the queue is emptied given the amount of allocated service bits.

Deﬁnition 1: Queue-n is said to be strongly stable if [13]

limsup

T →∞

∑

t=1

E [Q

(t)] < ∞, (5)

when there is no bound on the buffer size for any n.

When all queues are strongly stable in the system, the time-

average actual service rate equals the arrival rate, i.e.,

lim

T →∞

∑

t=1

˜µ

(t)= lim

T →∞

∑

t=1

(t), ∀n. (6)

Notice t hat the left-right-side is the time average of the real-

izations of the actual service rate, thus we do not need the

expectation to hold (6).

The achievable ergodic rate region

R is deﬁned as the convex

hull of all achievable rate points of n users. Denote all feasible

transmission schemes as

X and the transmission scheme π

∈

X , where s is the index for scheduling policies, is the user

scheduling scheme and the corresponding precoding scheme

with the rate of user-n at time t,

(H(t), π

(t)) = I (π

(t))log (1 +SINR (H(t), π

(t))), (7)

where I(π

(t)) is an indicator function which determines

whether user-n is scheduled, and SINR(H(t)) is the signal to

noise and interference ratio which is related to the channel

realization and the precoding scheme.

The user-n achievable

rate is deﬁned as the time-average of user rate

= lim

T →∞

∑

t=1

(H(t), π

(t)), ∀ n. (8)

Based on ergodicity, (8) equals

= E

{

(H, π

)

}

, ∀ n, (9)

where the expectation is taken over all possible channel gain

H(t) and possibly π

(t) when a randomized control policy is

considered. The achievable ergodic rate region can be charac-

terized as

R = coh



∈X

{

R :0≤

≤ E [R

(H, π

)]

}

, (10)

where

R is a N-dimensional region,

is its n-th component,

and “coh” denotes the closure of a convex hull.

Deﬁnition 2 (Throughput-Optimality): A scheduling scheme

is throughput-optimal if for any arrival rate point inside the

achievable ergodic rate region, the system can be stabilized by

the scheduling scheme.

Note that the throughput in this paper refers to the downlink

throughput, not concerning uplink throughput. We consider a

generic scenario where each user has its distinct block length

which denotes the number of consecutive channel uses that

the user-channel stays static, or also referred to as channel

coherence time. The block fading channel model is adopted

in this paper, where every user’s channel stays constant for

consecutive channel uses, and changes to another constant

according to an i.i.d. (over time and users) random process.

Denote by T

the channel coherence time of user-n, and let

T = {T

, T

,...,T

Notice that there are no units for both T

and T

, ∀k, since by deﬁnition, the block length in block fading

model equals channel coherence time multiplied by channel

coherence bandwidth. Therefore the block length describes

the channel coherence, both temporally and spectrally. Similar

notations have been used in [14], [2].

Here we assume that for every T

channel uses, the system

adopts one uplink channel training symbol (reciprocal channel

is considered here) to estimate the channel of user-n. By doing

this, we assume the BS obtains the perfect CSIT of user-n.

Hence, the number of concurrent scheduled users, denoted by

, equals the number of channel uses for channel estimation

numerically in each fading block. Note that this is actually

an optimistic assumption on the MU-MIMO system, since

normally we can only get a noisy version of the CSIT, and

the system has to do the channel training more than once to

reﬁne the estimation. Nonetheless our results can be extended

Explicit expressions of R

(H(t), π

(t)) will be shown later in Section IV.

The distinction of user block lengths is due to the fact that there are several

factors that can affect the block length of each user, such as distinct user-

mobility, scattering environment nearby, frequency offset and etc. We assume

the BS knows the channel coherence time apriori, since channel coherence

time is a second-order channel statistics, which can be regarded to be static for

a relatively long period.

剩余12页未读，继续阅读

weixin_38615397

粉丝: 6
资源: 895

动态信道捕获优化：MU-MIMO系统中的用户调度策略

MU-MIMO_sim.rar_MIMO多用户_MU MIMO MATLAB_mimo 信道建模_多用户 mimo_多用户MI

mmWave-MU-MIMO-master_massiveMIMO_MU-MIMO_MU_Massive-MIMO_mmwave

MU-MIMO.rar_MU-MIMO_cuong120_mimo_mu mimo_multi user

上下行MU-MIMO

mu-mimo工作原理

mu-mimo/ofdm

在MU-MIMO系统中，如何通过Lyapunov优化理论实现用户调度以提高系统效率？

OFDMA/802.11ax MU-MIMO

Linksys EA7500v2路由器如何通过4x4 MU-MIMO技术提高多设备连接的网络效率？

在MU-MIMO无线通信系统中，Lyapunov优化理论如何帮助我们设计出能够平衡CSI获取开销与系统效率的用户调度算法？

最新资源