矩阵与张量工具在时变数据挖掘中的应用

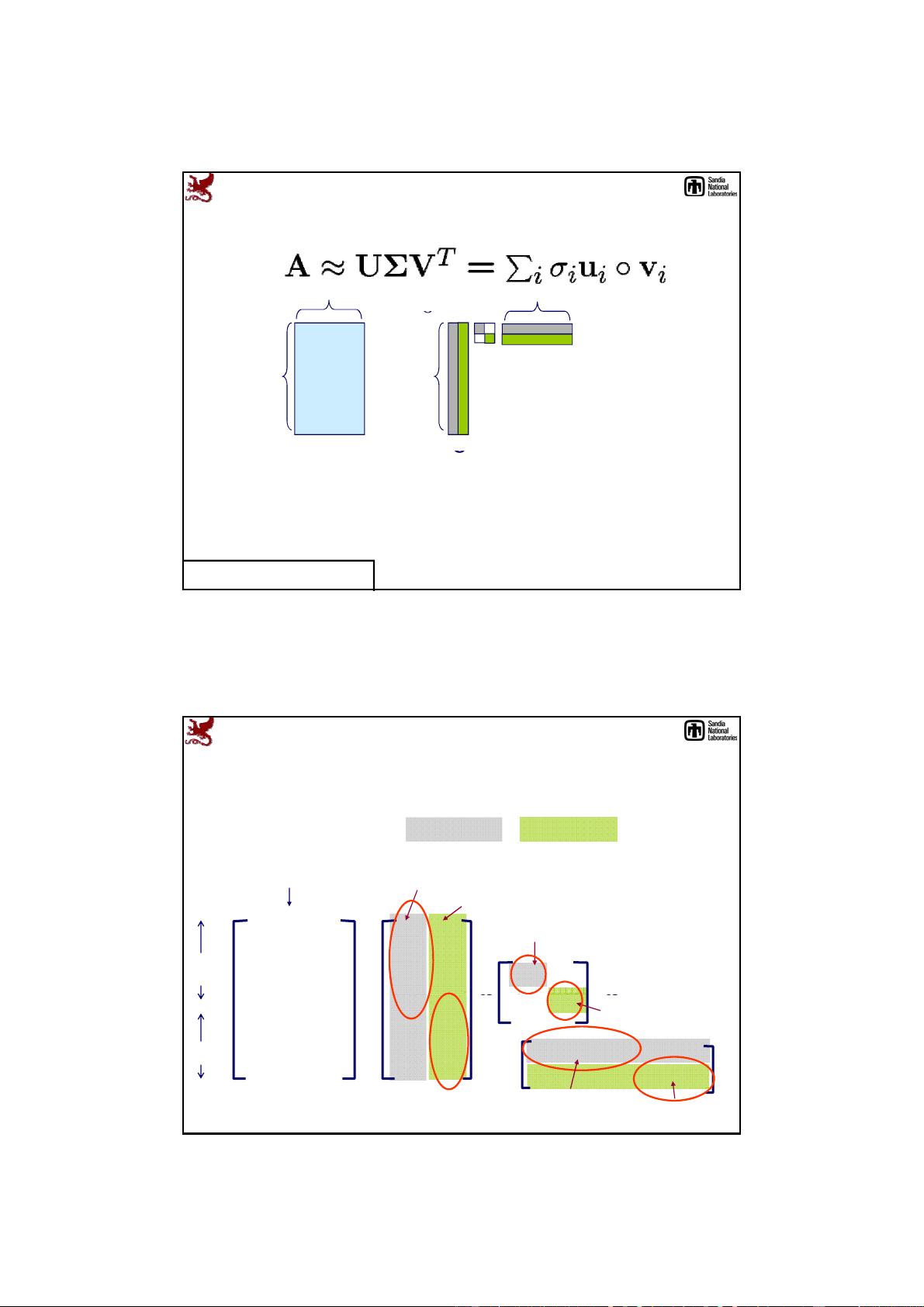
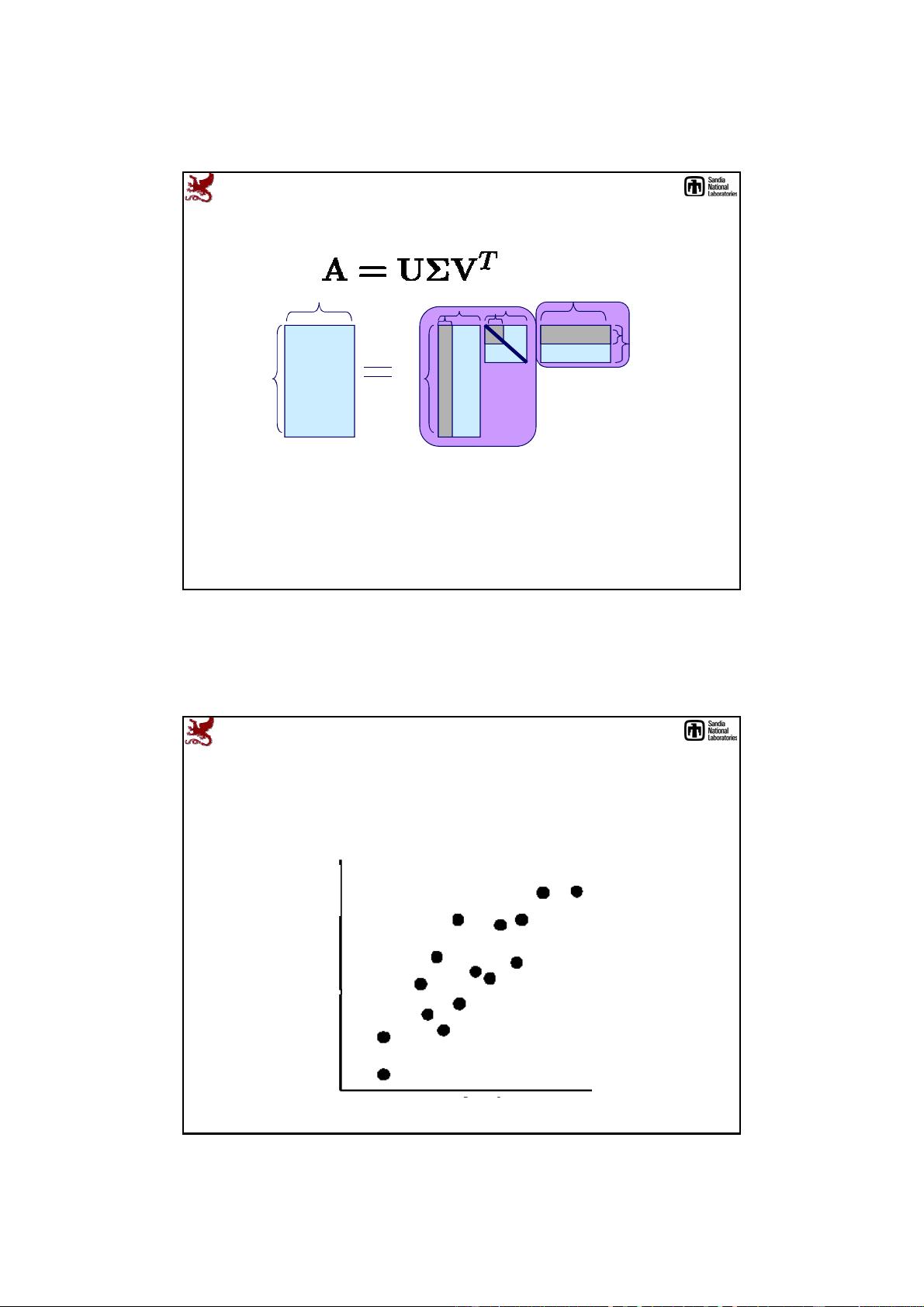
"本教程主要探讨如何使用矩阵和张量工具挖掘大规模随时间演变的数据，由Kolda在ICML上进行讲解。主要内容包括矩阵和张量理论在实际挖掘应用中的介绍，目标是发现模式、规则、聚类和异常值等。教程涵盖了矩阵分解方法如奇异值分解（SVD）、主成分分析（PCA）、网页排名算法（HITS、PageRank）、CUR分解、共聚类以及非负矩阵分解（NMF）。同时，也涉及张量分解技术，如Tucker分解、并行因子分析（PARAFAC）、DEDICOM，处理缺失值、非负性以及增量化的方法，并有相关应用和软件演示。本教程不涉及分类方法和核方法。" 在这个ICML教程中，Kolda深入介绍了在处理大规模时间序列数据时，如何利用矩阵和张量分析技术来提取有价值的信息。首先，矩阵工具被用来进行数据降维和特征提取，例如，奇异值分解（SVD）是一种广泛应用的矩阵分解技术，可用于数据压缩和噪声消除；主成分分析（PCA）则用于找到数据的主要成分，减少数据的维度同时保留大部分信息。此外，HITS（Hypertext Induced Topic Selection）和PageRank是两种网页排名算法，它们基于链接结构来评估网页的重要性。 CUR分解是另一种矩阵分解方法，它通过选择数据矩阵的一些行和列来近似整个矩阵，这对于保留原始数据的某些特性非常有用。共聚类是一种同时对行和列进行聚类的方法，常用于文档分类和协同过滤。非负矩阵分解（NMF）则是一种假设矩阵元素非负的分解方法，常用于图像处理、文本挖掘和推荐系统。 在张量工具部分，Tucker分解和并行因子分析（PARAFAC）是处理多维数据的主要手段，它们可以揭示数据的多阶结构。DEDICOM是另一种张量分解方法，特别适用于处理具有特定结构的高维数据。这些张量方法能够有效地处理缺失值，并且可以引入非负性约束，使得结果更符合现实世界中的物理或逻辑限制。此外，增量化策略使得在数据流不断更新的情况下也能实时地进行分析。 虽然这个教程不涉及分类方法和核方法，但它提供了一个全面的框架，用于理解和应用矩阵与张量工具进行大规模时间序列数据的挖掘。通过实际应用和软件演示，学习者将能够更好地理解这些工具如何在实践中解决问题，从而提升数据驱动的决策能力和洞察力。