HoroPCA：双曲空间中基于horospherical投影的主成分分析

版权申诉

171 浏览量更新于2024-07-06 收藏 1.08MB PDF 举报

HoroPCA: Hyperbolic Dimensionality Reduction via Horospherical Projections是一篇发表在计算机科学领域的论文，它探讨了如何将主成分分析（PCA）应用于超曲面数据。传统的PCA在欧几里得空间中非常有效，但随着超曲率几何在机器学习和数据挖掘中的应用逐渐增多，研究者们开始探索如何在非欧几里得环境中如双曲空间进行类似的降维方法。论文的主要贡献在于对PCA的三个关键元素进行了超曲面化。首先，他们提出了一个针对超曲面方向的参数化方法，这在传统的PCA中是基于欧几里得向量的。其次，他们定义了一种在超曲面上保持原始数据信息的投影方式，这涉及到对horospheres（双曲球面）的处理，这些结构在双曲几何中具有独特的性质。最后，他们引入了一个优化目标，即最大化投影解释的超曲面方差，这是与欧几里得空间中的方差相似的概念，但在双曲空间中具有不同的数学含义。 HoroPCA的优势在于它理论上更好地保留了原始数据的内在信息，特别是距离结构，相比于之前的PCA在超曲面上的直接应用。这是因为双曲空间的几何特性使得距离和角度关系不同于欧几里得空间，HoroPCA能够更精确地捕捉这种特性。此外，通过horospherical projections，HoroPCA能够在不损失太多信息的情况下，显著减少数据的维数，这对于处理高维、密集和稀疏的双曲数据集具有实际价值。论文的作者来自斯坦福大学，他们在计算机科学、计算和数学工程以及数学系工作，表明这项研究结合了理论基础和实践应用。HoroPCA为超曲面数据的分析提供了一种新颖且有效的降维工具，对于理解和处理双曲空间中的复杂数据集有着重要的意义。在未来的研究中，这种方法可能会推动更多领域，如社交网络分析、自然语言处理等，采用双曲几何来进行优化和模型构建。

Figure 3:

, y

are horospherical (green) projections of

x, y

. Proposition 3.4 shows

, y

) = d

(x, y)

. The distance

between the two geodesic (blue) projections is smaller.

3.2.1 Projecting onto K = 1 Directions

For

K = 1

, we have one ideal point

and base point

, and the geodesic hull

GH(b, p)

is just a geodesic

. Our goal is

to map every x ∈ H

to a point π

b,p

(x) on γ that has the same Busemann coordinate in the direction of p:

(x) = B

(π

b,p

(x)).

Since level sets of

(x)

are horospheres centered at

, the above equation simply says that

b,p

(x)

belongs to the

horosphere S(p, x) centered at p and passing through x. Thus, we deﬁne:

b,p

(x)

= γ ∩ S(p, x). (3)

Another important property that

b,p

(·)

shares with orthogonal projections in Euclidean spaces is that it preserves

distances along a direction – lengths of geodesic segments that point to p are preserved after projection (Fig. 3):

Proposition 3.4. For any x ∈ H

, if y ∈ GH(x, p) then:

(π

b,p

(x), π

b,p

(y)) = d

(x, y).

Proof.

This follows from the remark in Section 2.2 about horospheres: every geodesic going through

is orthogonal to

every horosphere centered at

, and every orthogonal geodesic segment connecting concentric horospheres has the same

length (Fig. 2). In this case, the segments from

and from

b,p

(x)

b,p

(y)

are two such segments, connecting

S(p, x) and S(p, y).

3.2.2 Projecting onto K > 1 Directions

We now generalize the above construction to projections onto higher-dimensional submanifolds. We describe the main

ideas here; Appendix A contains more details, including an illustration in the case K = 2 (Fig. 5).

Fix a base point

b ∈ H

and

K > 1

ideal points

, . . . , p

}

. We want to deﬁne a map from

GH(b, p

, . . . , p

) that preserves the Busemann coordinates in the directions of p

, . . . , p

, i.e.:

(x) = B



b,p

,...,p

(x)



for every j = 1, . . . , K.

As before, the idea is to take the intersection with the horospheres centered at p

’s and passing through x:

b,p

,...,p

: H

→ M

x 7→ M ∩ S(p

, x) ∩ · · · ∩ S(p

, x).

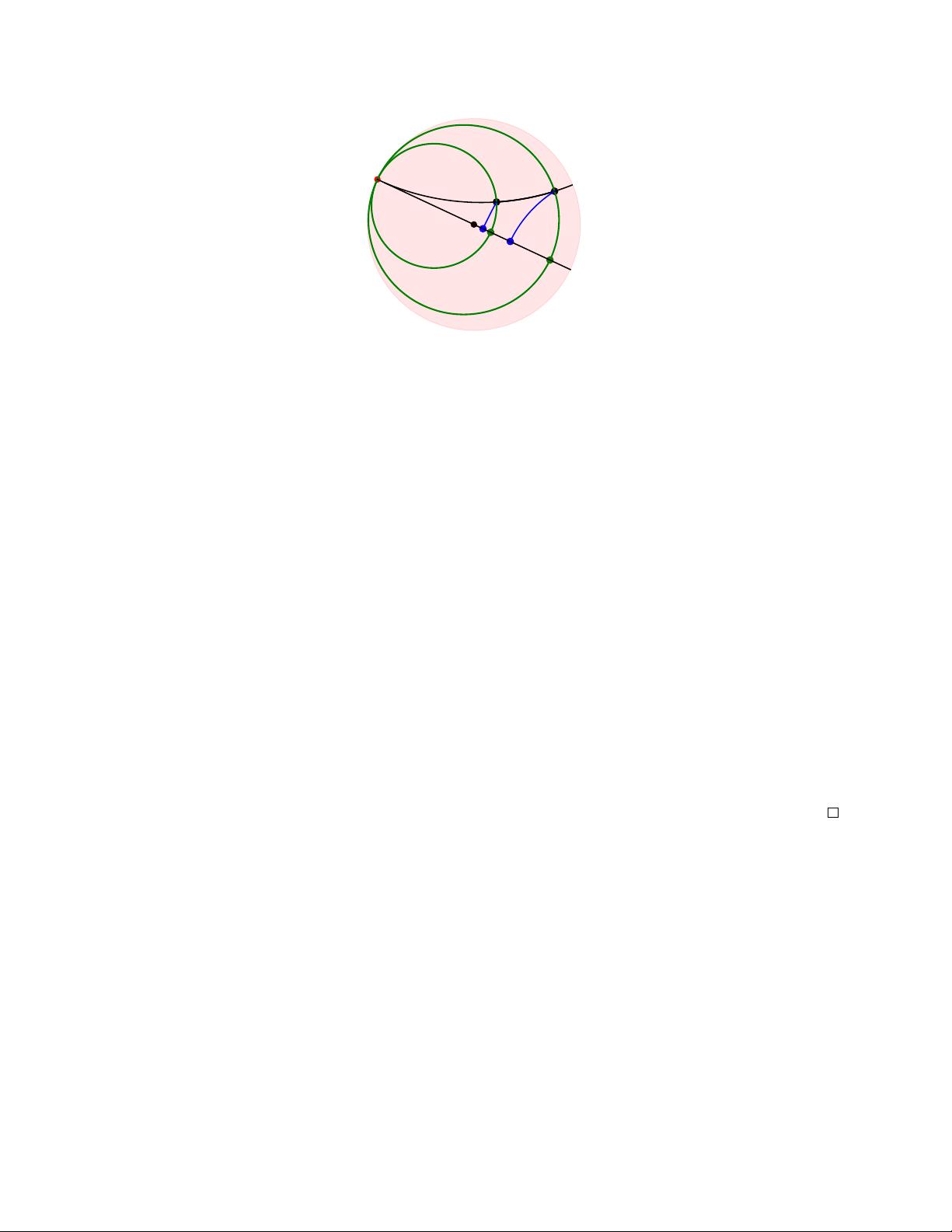
It turns out that this intersection generally consists of two points instead of one. When that happens, one of them will be

strictly closer to the base point b, and we deﬁne π

b,p

,...,p

(x) to be that point.

As with Proposition 3.4,

b,p

,...,p

(·)

preserves distances along

-dimensional manifolds (Corollary A.10). In contrast,

geodesic projections in hyperbolic spaces never preserve distances (except between points already in the target):

Proposition 3.5.

Let

M ⊂ H

be a geodesic submanifold. Then every geodesic segment of distance at least

from

gets at least cosh(r) times shorter under the geodesic projection π

(·) to M:

length(π

(I)) ≤

cosh(r)

length(I).

In particular, the shrink factor grows exponentially as the segment I moves away from M.

The proof is in Appendix B.

Computation

Interestingly, horosphere projections can be computed without actually computing the horospheres.

The key idea is that if we let

P = GH(p

, . . . , p

)

be the geodesic hull of the horospheres’ centers, then the intersection

S(p

, x) ∩ · · · ∩ S(p

, x)

is simply the orbit of

under the rotations around

. (This is true for the same reason that

spheres whose centers lie on the same axis must intersect along a circle around that axis). Thus,

b,p

,...,p

(·)

can be

viewed as the map that rotates x around until it hits M. It follows that it can be computed by:

1. Find the geodesic projection c = π

(x) of x onto P .

2. Find the geodesic α on M that is orthogonal to P at c.

3. Among the two points on α whose distance to c equals d

(x, c), returns the one closer to b.

The detailed computations and proof that this recovers horospherical projections are provided in Appendix A.

3.3 Intrinsic Variance Objective

In Euclidean PCA, directions are chosen to maximally preserve information from the original data. In particular, PCA

chooses directions that maximize the Euclidean variance of projected data. To generalize this to hyperbolic geometry,

we deﬁne an analog of variance that is intrinsic, i.e. dependent only on the distances between data points. As we will

see in Section 4, having an intrinsic objective helps make our algorithm location (or base point) independent.

The usual notion of Euclidean variance is the squared sum of distances to the mean of the projected datapoints.

Generalizing this is challenging because non-Euclidean spaces do not have a canonical choice of mean. Previous works

have generalized variance either by using the unexplained variance or Fr

echet variance. The former is the squared sum

of residual distances to the projections, and thus avoids computing a mean. However, it is not intrinsic. The latter is

intrinsic [10] but involves ﬁnding the Fr

echet mean, which is not necessarily a canonical notion of mean and can only

be computed by gradient descent.

Our approach uses the observation that in Euclidean space:

(S) =

x∈S

kx − µ(S)k

x,y∈S

kx − yk

Thus, we propose the following generalization of variance:

(S) =

x,y∈S

(x, y)

. (4)

This function agrees with the usual variance in Euclidean space, while being a function of distances only. Thus it is

well deﬁned in non-Euclidean space, is easily computed, and, as we will show next, has the desired invariance due to

isometry properties of horospherical projections.

剩余30页未读，继续阅读

易小侠

粉丝: 6589
资源: 9万+

HoroPCA：双曲空间中基于horospherical投影的主成分分析

MATLAB双曲抛物面.rar_fingeri88_regulardzg_一个基于maltab的双曲抛物面

Hyperbolic_Chirp_chirp时频_模拟信号_双曲啁啾信号_信号分析_时频分析_

matlab.rar_-baijiahao_区分图像噪声_去噪_双曲型差分_斑点噪声MATLAB

双曲几何基础—-Hyperbolic Geometry

hyperbolic:双曲时间室

厄米_双曲正弦_高斯光束的M_2因子

matlab的双曲线代码-hyperbolic_orbifolds:实施SIGGRAPHAsia2016论文“双曲OrbifoldTutte嵌

Desktop_用于双曲型方程的差分运算_

matlab复变函数指数函数代码-Hyperbolic_Exponential-CORDIC:迭代离散数学方法以实现精确的双曲指数输出

hyperbolic:用于构建和绘制双曲几何的 Python 3 库

最新资源