数据降维神器：主成分分析（PCA）在调查数据分析中的应用

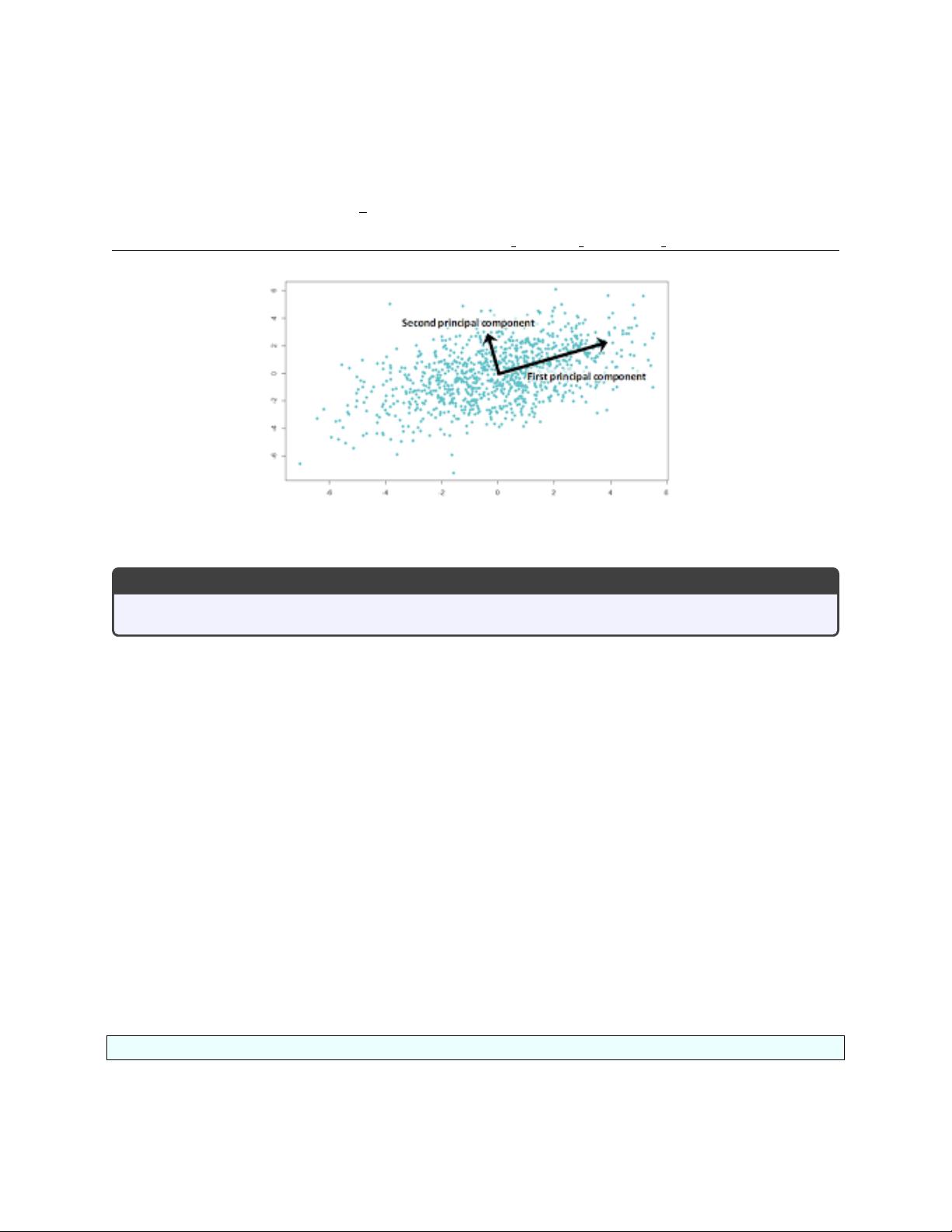
"Principal Component Analysis (PCA) 是一种强大的统计学方法，在机器学习领域 ML2022 中被广泛讨论。这份名为 "pca_lecture.pdf" 的资料详细介绍了在处理大量数据时如何寻找和提取数据的主要趋势和特征。当我们面对像调查问卷这样包含众多问题（如50个问题）的数据集时，每个个体的回答可能千差万别，但可能隐藏着某些模式，比如性别、年龄或政治倾向等。 PCA的核心目标是找到一组相互正交（即不相关的）基础向量，这些向量能够尽可能地捕捉数据集中的大部分信息。通过这种方式，我们试图将复杂的数据压缩到最少的维度中，便于理解和分析。例如，如果一个调查问卷有50个问题，直接计算每个问题的答案平均值和方差可能会非常繁琐，而PCA可以帮助我们发现其中的关键因素，用少数几个主成分来解释大部分答案的变异。 在进行PCA时，数据通常被表示为一个大型的数值矩阵，这使得我们可以利用线性代数工具来执行降维操作。通过对矩阵进行特征值分解，我们可以得到一组按重要性排序的主成分，每个主成分对应于原始数据的一个线性组合。第一主成分通常与数据的方差最大，第二主成分则保留了剩余方差中最大的部分，以此类推。 通过这种方式，PCA不仅可以简化数据表示，还可以用于数据预处理，例如在高维数据中减少噪声、降低计算复杂度，或者在数据可视化时进行有效的投影，使得复杂的多维数据在二维或三维空间中更容易理解。在实际应用中，PCA在诸如图像处理、生物信息学、金融数据分析等领域都有广泛的应用，是数据挖掘和机器学习中不可或缺的一部分。" 这份讲座提供了深入浅出的PCA概念介绍和实用技巧，对于理解并运用这一工具分析实际数据具有重要的参考价值。