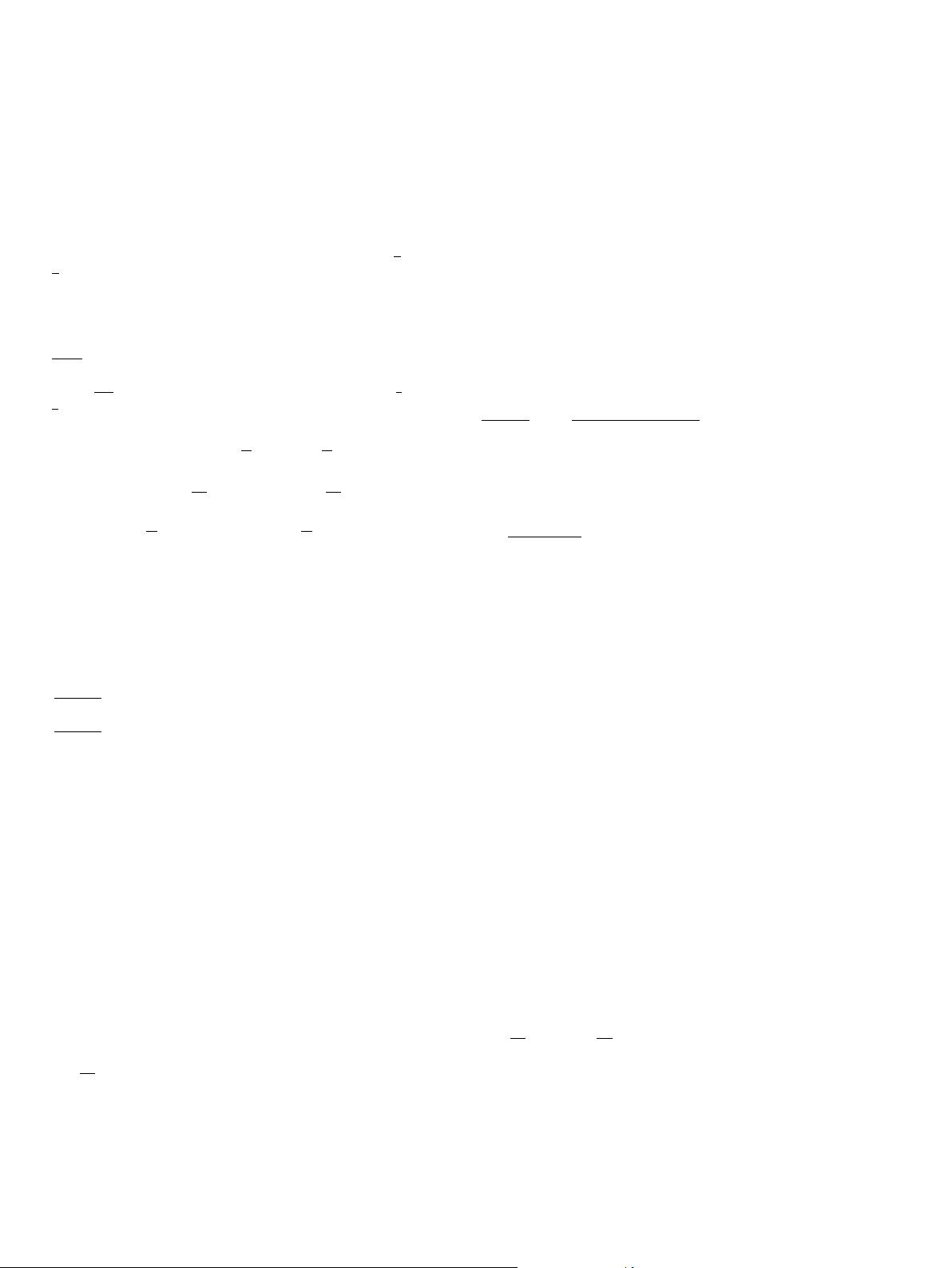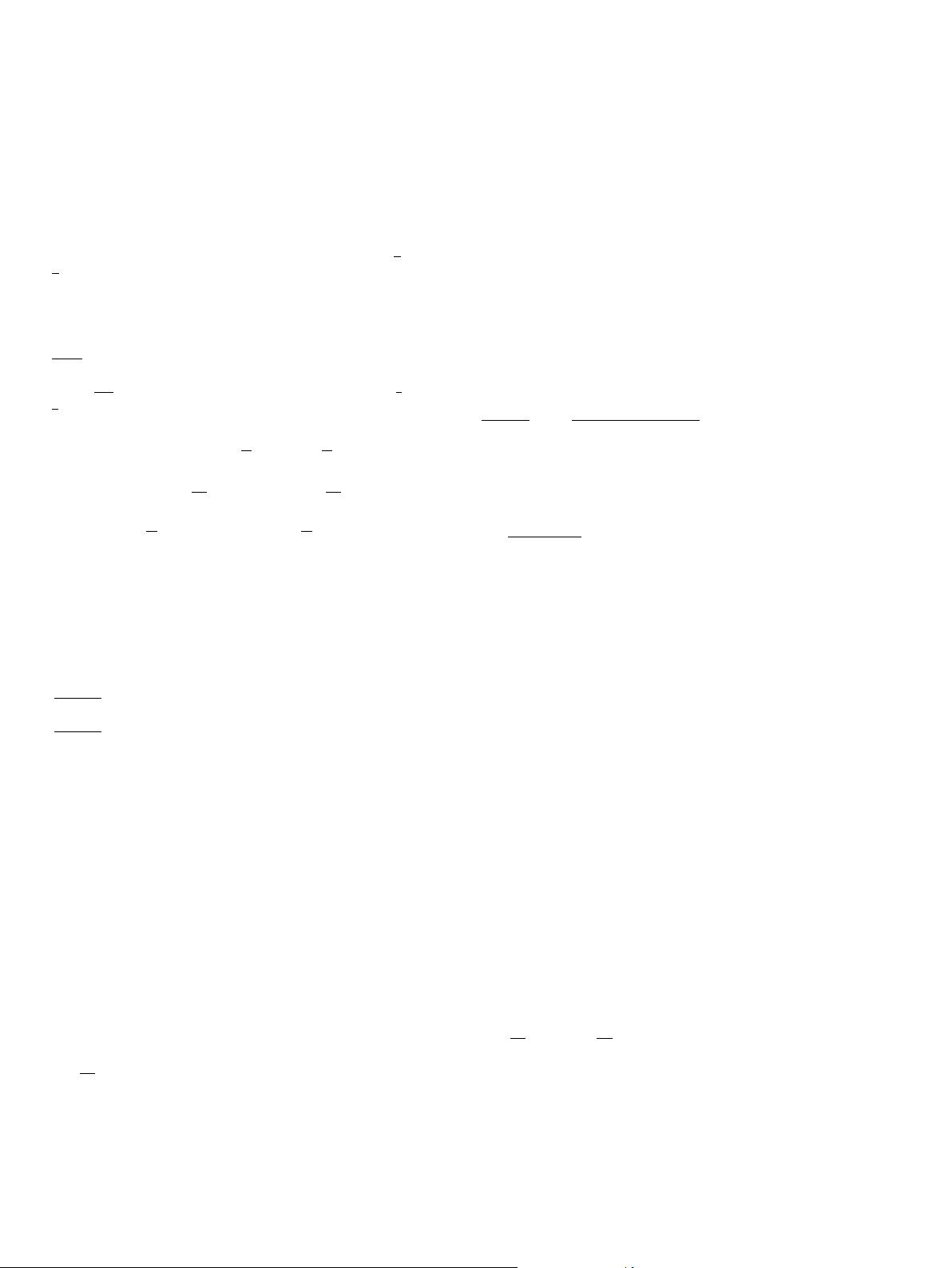
3.2. Computation of scale, rotation and translation transformations
Step 1 of the SICP algorithm can be solved by many methods
such as the nearest point search algorithm based on Delaunay tri-
angulations [17]; hence step 2 is the key step. To compute the new
scale, rotation and translation transformations, the following lem-
ma is given first to eliminate the translation transformation:
Lemma 1. Given two m–D point sets f
~
q
i
g
N
i¼1
and f
~
n
i
g
N
i¼1
, the function
Fð
~
tÞ¼
P
N
i¼1
k
~
q
i
þ
~
t
~
n
i
k
2
2
has the minimum when
~
t ¼
1
N
P
N
i¼1
~
n
i
1
N
P
N
i¼1
~
q
i
.
Proof. If Fð
~
tÞ reaches the minimum, it must satisfy the following
requirement:
dFð
~
tÞ
d
~
t
¼ 0
As
dFð
~
tÞ
d
~
t
¼ 2
P
N
i¼1
ð
~
q
i
þ
~
t
~
n
i
Þ¼0, we can obtain
~
t ¼
1
N
P
N
i¼1
~
n
i
1
N
P
N
i¼1
~
q
i
. h
According to Lemma 1, if minimizing FðS; RÞ¼
P
N
p
i¼1
k
ðRS
~
p
i
þ
~
tÞ
~
m
c
k
ðiÞ
k
2
2
, we get
~
t ¼
1
N
p
P
N
p
i¼1
~
m
c
k
ðiÞ
1
N
p
P
N
p
i¼1
RS
~
p
i
. Hence,
FðS; RÞ¼
X
N
p
i¼1
RS
~
p
i
1
N
p
X
N
p
i¼1
~
p
i
!
~
m
c
k
ðiÞ
1
N
p
X
N
p
i¼1
~
m
c
k
ðiÞ
!
2
2
Let
~
q
i
,
~
p
i
1
N
p
P
N
p
i¼1
~
p
i
and
~
n
i
,
~
m
c
k
ðiÞ
1
N
p
P
N
p
i¼1
~
m
c
k
ðiÞ
, therefore,
FðS; RÞ¼
X
N
p
i¼1
RS
~
q
i
~
n
i
2
2
¼
X
N
p
i¼1
~
q
T
i
S
2
~
q
i
2
X
N
p
i¼1
~
n
T
i
RS
~
q
i
þ
X
N
p
i¼1
~
n
T
i
~
n
i
ð11Þ
To minimize Eq. (11), we can recover the following partial dif-
ferential equations to compute scale and rotation transformations:
@FðS; RÞ
@R
¼ 0 ð12Þ
@FðS; RÞ
@S
¼ 0 ð13Þ
3.2.1. Rotation computation
The rigid registration between two paired point sets is a well-
studied problem in the literature. Many closed-form methods are
known to be used to compute the rigid transformation: singular va-
lue decomposition (SVD) [18], unit quaternions [19], orthonormal
matrices [20] and dual quaternions [21]. An overview of these meth-
ods and a comparative analysis can be found in [22]. As the SVD algo-
rithm still works even when S is considered, we will detail the
method to compute rotation transformation of Eq. (12) as follows.
For any given S, the necessary condition of minimizing FðS; RÞ is
Eq. (12) which cannot be computed easily, but according to Eq.
(11), minimizing FðS; RÞ is equivalent to maximizing
P
N
p
i¼1
~
n
T
i
RS
~
q
i
,
which can be solved similar to that Arun [18] had proposed, thus
we only give the conclusion here.
1. Calculate m m matrix H and its SVD.
H ¼
1
N
p
X
N
p
i¼1
S
~
q
i
~
n
T
i
ð14Þ
H ¼ UKV ð15Þ
2. Calculate the rotation matrix R.
(a) If detðVU
T
Þ¼þ1; VU
T
is a rotation:
R ¼ VU
T
ð16Þ
(b) If detðVU
T
Þ¼1; VU
T
is a reflection:
(i) If one of the singular values of H is zero, the desired rota-
tion can be calculated as follows:
R ¼ V
I
m1
0
0 1
U
T
ð17Þ
(ii) If none of the singular values of H is zero, we go to a RAN-
SAC-like technique.
3.2.2. Scale computation
Suppose that E
j
¼ diagð0; ...; 0; 1; 0; ...; 0Þ; ðj ¼ 1; 2; ...; mÞ is a
diagonal matrix where the j
th
element is one, but others are zero.
They are the basis of the matrix S, and then Eq. (13) can be ex-
pressed as follows:
@FðS; RÞ
@S
¼ lim
t!0
FðS þ tE
j
; RÞFðS; RÞ
t
¼ 2
X
N
p
i¼1
~
q
T
i
SE
j
~
q
i
2
X
N
p
i¼1
~
n
T
i
RE
j
~
q
i
¼ 0 ð18Þ
From Eq. (18), we get
s
j
¼
P
N
p
i¼1
~
n
T
i
RE
j
~
q
i
P
N
p
i¼1
~
q
T
i
E
j
~
q
i
ð19Þ
1. If s
j
is any arbitrary number, we obtain the scale of SICP with
unbounded scale:
s
j
¼
X
N
p
i¼1
~
n
T
i
RE
j
~
q
i
,
X
N
p
i¼1
~
q
T
i
E
j
~
q
i
ð20Þ
2. If s
j
2½a
j
; b
j
, according to Eq. (11), the function is known to be a
parabola with respect to s
j
and its symmetry axis parallels to
vertical axis, so the minimum can be achieved at the point
which is nearest to the vertex of this parabola, hence we get
the scale s
j
of the SICP algorithm:
s
j
¼ arg min
s2½a
j
;b
j
s
X
N
p
i¼1
~
n
T
i
RE
j
~
q
i
,
X
N
p
i¼1
~
q
T
i
E
j
~
q
i
ð21Þ
3.2.3. Termination
After the computation of rotation and scale transformations
above, we check whether the change of S is less than
e
or a maxi-
mum number of iterations is reached. If it does, we switch outside
the loop, otherwise we continue the iteration.
3.2.4. Translation computation
If rotation and scale transformations are computed, according
to Lemma 1, we calculate
~
t
k
:
~
t
k
¼
1
N
p
X
N
p
i¼1
~
m
c
k
ðiÞ
1
N
p
X
N
p
i¼1
R
k
S
k
~
p
i
ð22Þ
From what is discussed above, the scale, rotation and transla-
tion transformations of Eq. (10) are computed. Therefore, the
whole SICP algorithm is reasonably drawn out as follows.
Input: Two point sets P , f
~
p
i
g
N
p
i¼1
and M , f
~
m
i
g
N
m
i¼1
.
Initialize: Scale matrix S
0
, rotation matrix R
0
, translation vector
~
t
0
and the scale boundary are initialized by using covariance
matrices of point sets, which is stated in Section 4.
444 S. Du et al. / J. Vis. Commun. Image R. 21 (2010) 442–452