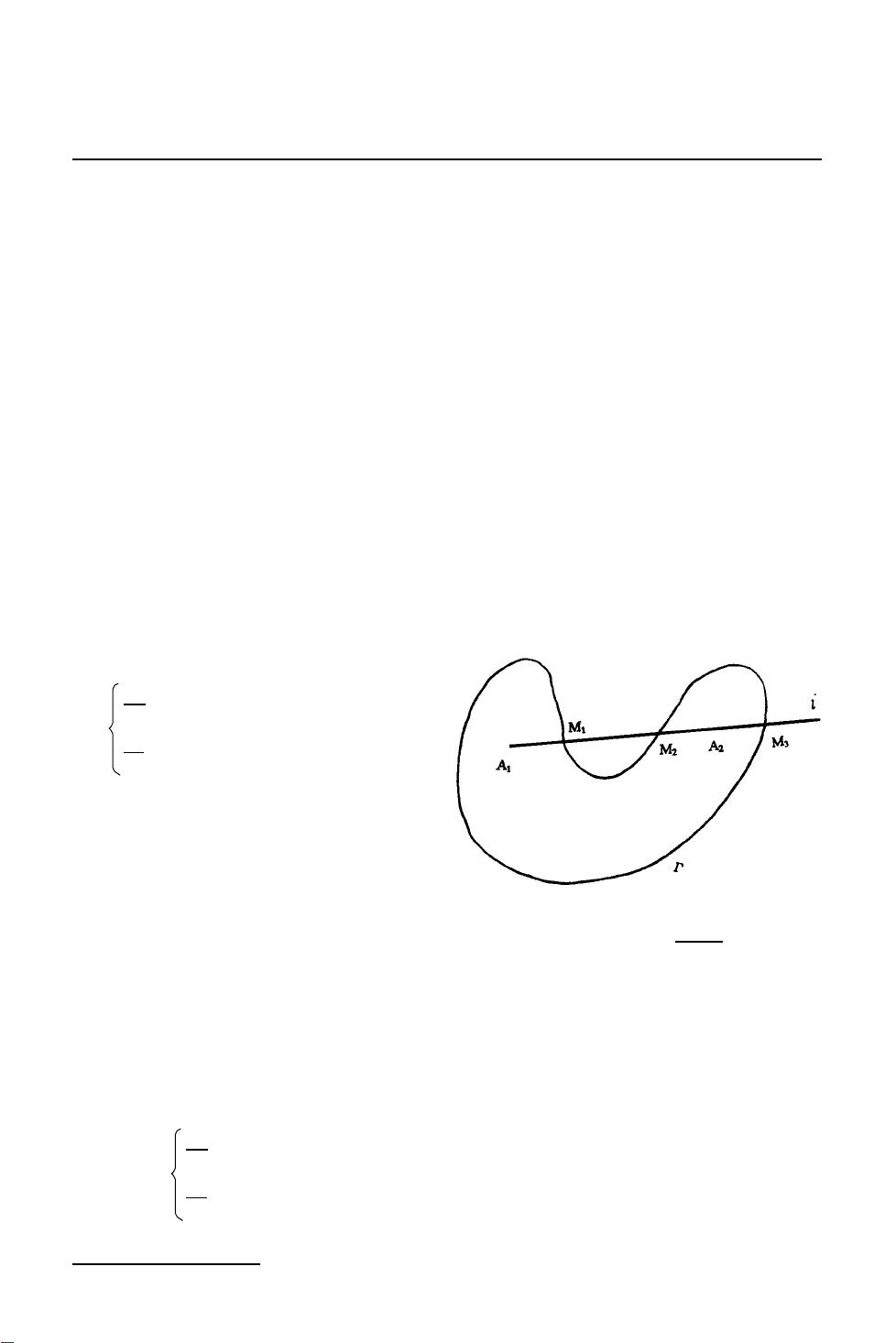三维凸性分析：三次平面多项式系统闭轨的凸性探讨(1998)

本文主要探讨了平面多项式系统确定的闭曲线在实际工程应用中的凸性问题，特别是针对次数不超过三次的多项式系统。在齿轮设计等场景中，确保闭合曲线的凸性对于确保机械结构的稳定性和性能至关重要。论文首先给出了凸集和凸曲线的定义，强调了闭合曲线的凸性是通过判断任意两点间连线是否完全位于区域内部来确定的。 引理部分表明，对于非凸的闭合集合Ω，总能找到一条从Ω内部出发的射线，至少与Ω的边界曲线相交于三个点。这个引理为后续的分析提供了关键推论。作者利用这个引理证明了一个重要定理：当多项式的阶数n小于等于2时，系统(1)定义的所有闭轨都是凸的。他们采用了反证法，假设存在非凸闭轨，然后通过平移坐标和极坐标变换，将问题简化到一个从原点出发的射线与闭轨的交点个数，进而得出矛盾。 当n=2时，由于多项式的低次特性，闭轨的形状易于控制，不容易出现非凸的情况。然而，对于更高次的多项式系统(n>2)，情况可能会变得复杂，可能需要更复杂的理论分析和计算方法来确保闭轨的凸性。这篇论文提供了一个基础框架，对于理解如何处理这类几何约束问题具有重要意义，但并未深入讨论n>2时的具体方法。 这篇文章在凸性理论和多项式系统动态系统之间架起了一座桥梁，对于从事齿轮设计、控制系统或者其他依赖于闭曲线凸性的领域的工程师和技术人员来说，它提供了一种理论指导，帮助他们在实践中判断和优化设计。同时，这也为数学和计算机科学领域的理论研究者提供了实际问题的背景和挑战，促进了理论与实际应用的结合。