MATLAB实现：快速掌握傅立叶变换基础与函数转换

傅立叶变换是一种在信号处理、通信工程和数学等领域广泛应用的数学工具，用于将一个时间域或空间域的信号转换为频域表示，从而揭示信号的频率成分。本文档详细介绍了如何使用MATLAB来实现傅立叶变换，特别是针对几种常见的数学函数，如阶跃函数、符号函数、矩形函数、三角函数、Sinc函数、高斯函数、园域函数等。 在MATLAB中，傅里叶变换的计算通常涉及到复数和复数运算，因为傅里叶变换涉及解析函数的解析延拓。文档首先介绍了几个基本概念，如脉冲函数及其性质，以及与卷积相关的定义，包括定义、物理意义和性质。卷积在傅立叶变换中扮演着关键角色，它是信号处理中的核心概念，表示的是两个函数的混合结果在频域的对应关系。 接下来，文档讨论了空间频率的概念，即信号频率在空间域的表现，这对于理解信号在不同空间位置的频率特性至关重要。傅里叶变换本身有严格的定义和存在条件，包括标准傅里叶变换（适用于实函数）和广义傅里叶变换（对复函数）。对于不同类型的函数，如实函数、奇函数、偶函数以及可分离函数，它们的傅里叶变换具有独特的性质。此外，文中还提到了傅里叶-Bessel变换，这是一种特定情况下简化傅里叶变换的方法。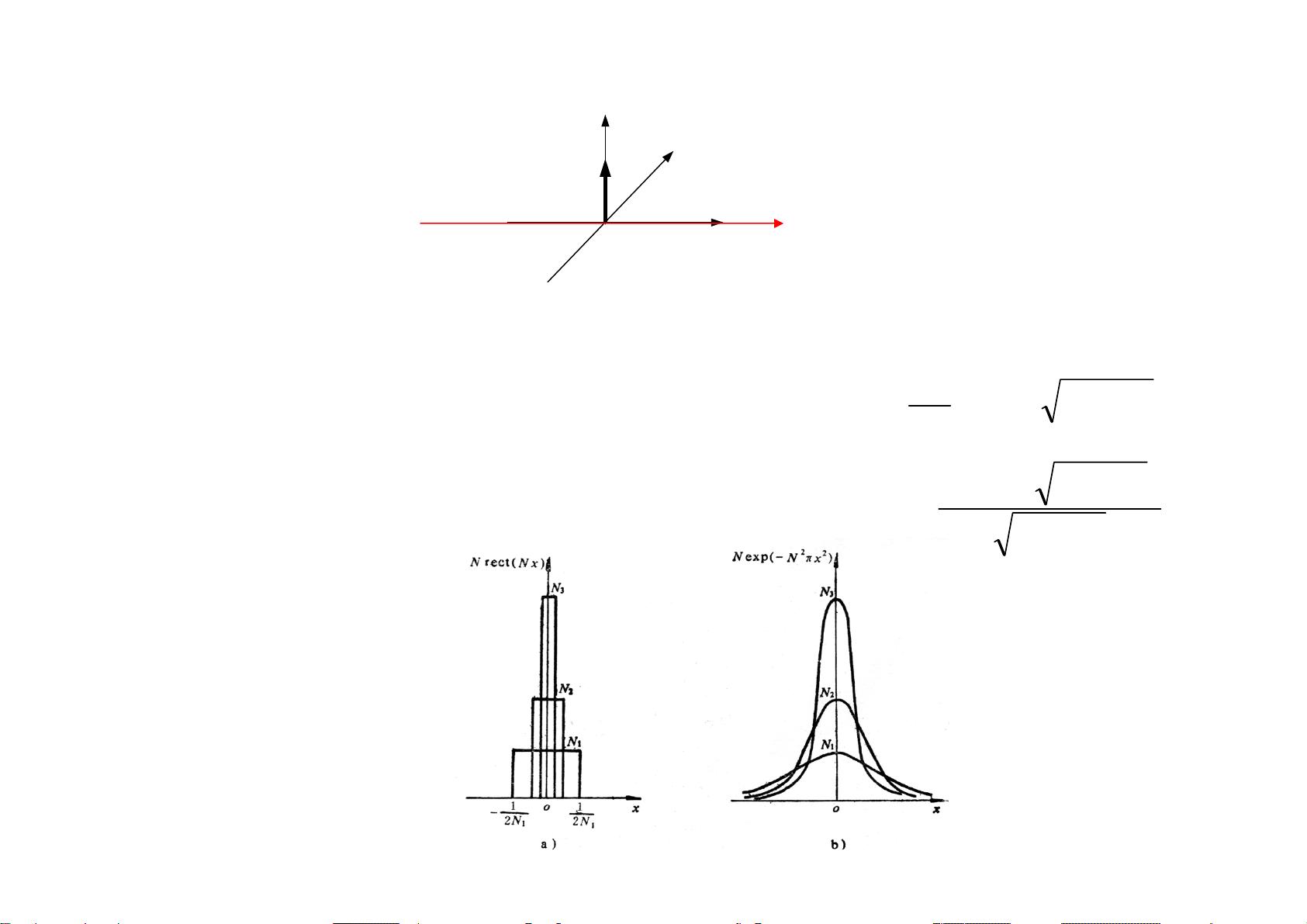 在具体操作层面，文档展示了如何通过MATLAB代码计算阶跃函数和符号函数的傅里叶变换，例如阶跃函数`step`函数的定义和其在MATLAB中的实现。这些函数的傅里叶变换有助于理解基础函数在频域的表示。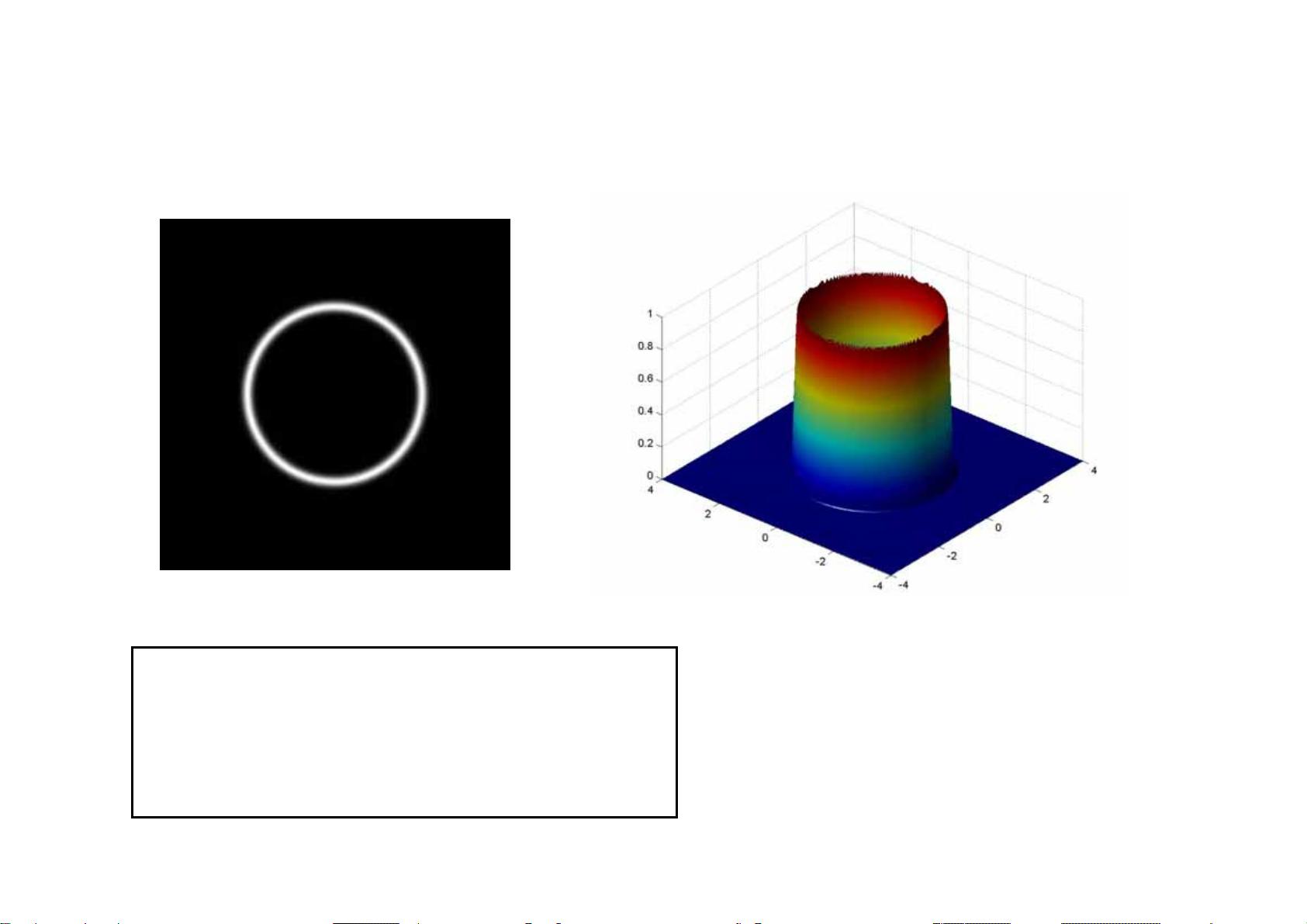 最后，文档涵盖了实际应用中的内容，如几种常见图形的傅里叶变换，以及傅里叶变换的数值实现。这部分内容不仅提供了理论背景，也强调了实践操作的技巧，帮助读者掌握如何在MATLAB环境中高效地进行傅立叶变换的计算。 该文档是MATLAB用户学习傅里叶变换的一个实用指南，涵盖了傅里叶变换的基本原理、函数实例以及在MATLAB中的具体实现步骤，对于信号处理和数值分析的学习者来说，是一份不可或缺的参考资料。