线性方程组求解方法探究

线性方程组是数学中的基础概念，广泛应用于自然科学、工程学、经济学等多个领域。解决这类问题的方法多种多样，本报告主要探讨了其中的几种经典方法：高斯消去法（Gauss Elimination）、LU分解法（LU Factorization），以及在特定情况下的三对角矩阵求解。 首先，高斯消去法是最常见的线性方程组求解方法之一。它通过一系列矩阵的初等行变换将原方程组的系数矩阵A转换为上三角矩阵U，然后通过回代求解上三角方程组得到解。在这个过程中，分为无交换消去（Nopivoting）和有交换消去（包括部分交换Pivoting和全交换Pivoting）。无交换消去法简单但稳定性较差，当遇到主元为0或近似为0的情况时，会导致计算失效。为了提高稳定性，通常会采用部分或全交换策略，即选择每一步的主元时考虑最大绝对值，以避免数值不稳定性。 高斯消去法的基本步骤如下： 1. 输入增广矩阵[B = [A | b]]，A为系数矩阵，b为常数向量。 2. 应用初等行变换，逐步将A变为上三角矩阵U，同时保持B的列对应关系不变。 3. 对上三角矩阵U求解，通常采用回代法，即从最下一行开始，逐次求解未知数。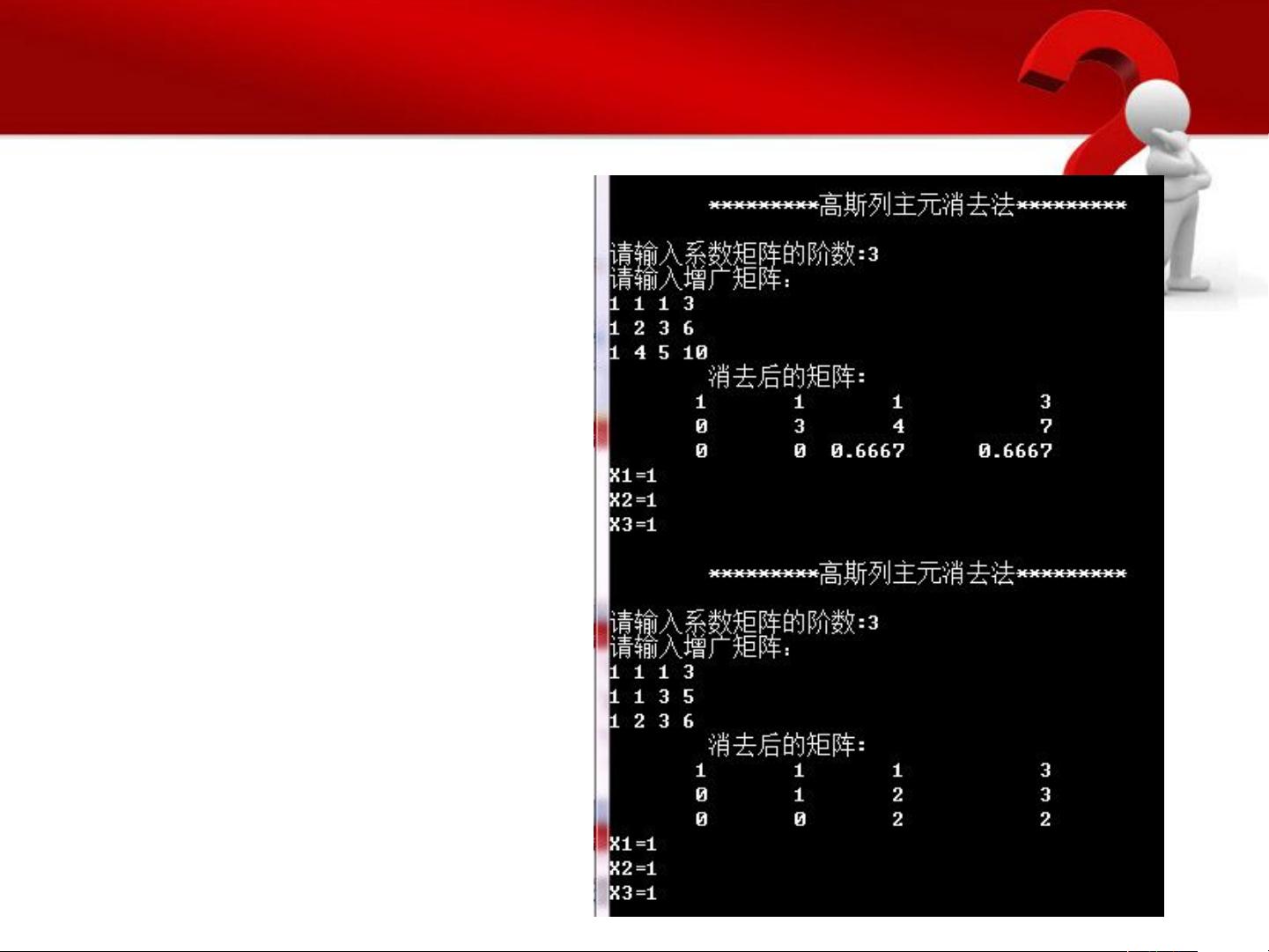 在实际编程实现中，通常使用C++或其他编程语言进行，如示例代码中所示，定义矩阵a和解向量x，然后执行消元操作。注意，由于浮点数的精度问题，实际编程中可能需要考虑舍入误差。 接着，LU分解法是另一种常用的求解线性方程组的方法。它将系数矩阵A分解为两个矩阵L（下三角矩阵）和U（上三角矩阵）的乘积，即A = LU，然后分别求解Ly = b和Ux = y。这种方法在数值稳定性上优于简单的高斯消去法，尤其适用于需要反复求解同一系数矩阵的不同右端项b的情况下。 对于特殊情况，如三对角矩阵，其求解方法更为简便，可以利用高斯-约旦消元或者迭代法（如Gauss-Seidel或Jacobi方法）高效求解，因为这类矩阵结构特殊，计算量和复杂度显著降低。 线性方程组的求解方法根据实际问题和计算环境的不同，可以选择不同的策略。在理解各种方法的基础上，结合实际需求和数值稳定性考虑，才能有效地解决问题。而编程实现时，需要注意数值计算的精确性和效率优化，以达到理想的求解效果。