有限状态自动机与正规表达式详解：Thompson构造法与转换

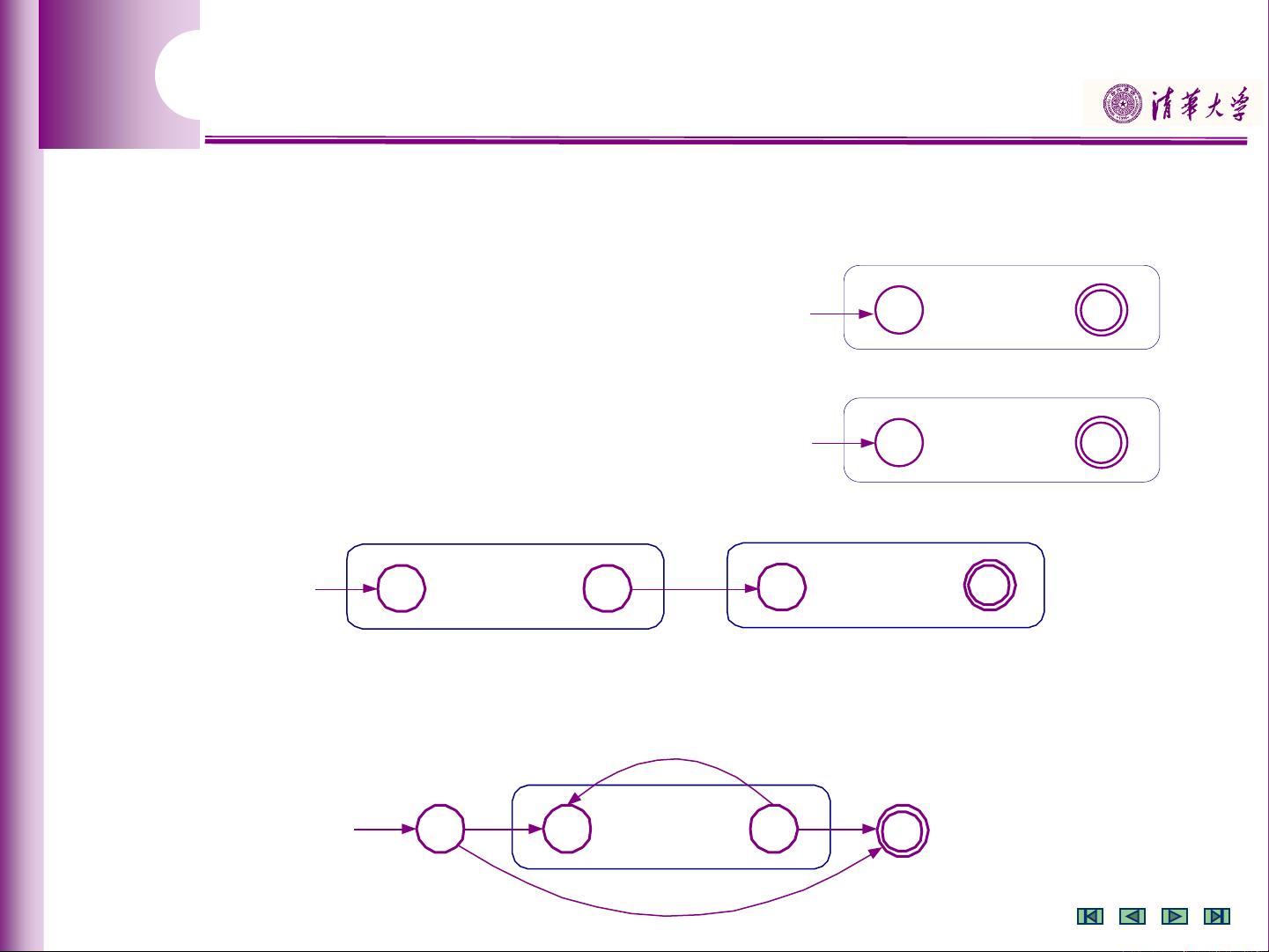
本资源主要探讨了"形式语言与自动机"中的第五讲内容，即有限状态自动机与正规表达式的关联。有限状态自动机（Finite Automaton，简称FA）是理论计算机科学中的基础概念，它们用于识别特定的输入序列是否属于某个预先定义的语言或模式。本讲详细介绍了几种关键概念和转换算法： 1. 有限状态自动机与正规表达式的关系： - 定理表明，如果一个语言L由正规表达式R表示，那么存在一个ε-NFA（带有空字符的非确定有限自动机）E，它的语言L(E)等于L(R)，即两者表示的是相同的语言。证明过程通常是构造性的，例如通过Thompson构造法，根据正规表达式的结构逐步构建等价的自动机，确保满足特定条件，如只有一个终态、无弧进入初态和无弧离开终态。 2. 构造方法： - Thompson构造法则是一种递归的方法，通过合并子表达式来构造自动机。例如，对于`R+S`，构造为两个子自动机S和R之间插入ε-弧；对于`RS`，将R和S串联起来，并在它们之间加上ε-弧。 - 对于星号`*`，表示零个或多个重复，可以用一个循环状态和适当的转移来实现；对于`1*0(0+1)*`这样的例子，会涉及到更复杂的组合和递归应用。 3. 从DFA到正规表达式转换： - 提到如果一个语言L是某个确定有限自动机DFA的语言，那么可以构造一个正规表达式R，使得L(R) = L(D)。这里有两种构造方法：路径叠代法（Kleene构造法）和状态消去法，通过这些方法将DFA的状态和转换映射为正规表达式的规则。 4. 举例： - 通过具体例子展示如何使用Thompson构造法将正规表达式转化为等价的ε-NFA，例如 `(0+1)*` 和 `1*0(0+1)*` 的构造过程。 总结来说，本资源深入剖析了有限状态自动机与正规表达式之间的转换原理和构造方法，这对于理解语言理论和设计计算机算法具有重要意义。学习者可以通过这个讲义了解如何将一种形式化表示转换为另一种，并利用它们在实际编程和系统设计中处理字符串匹配问题。