二叉树遍历算法详解：先序、中序、后序

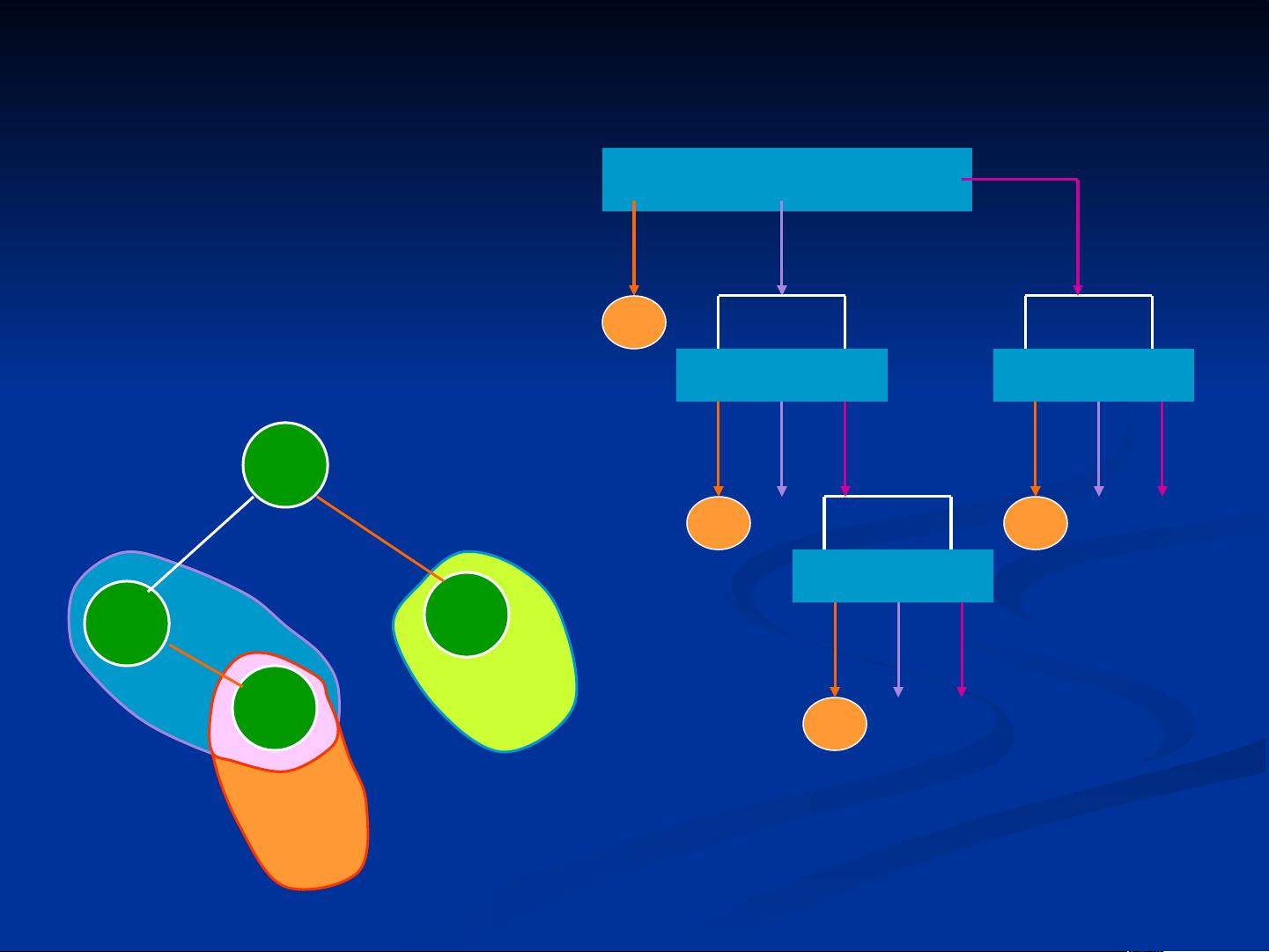
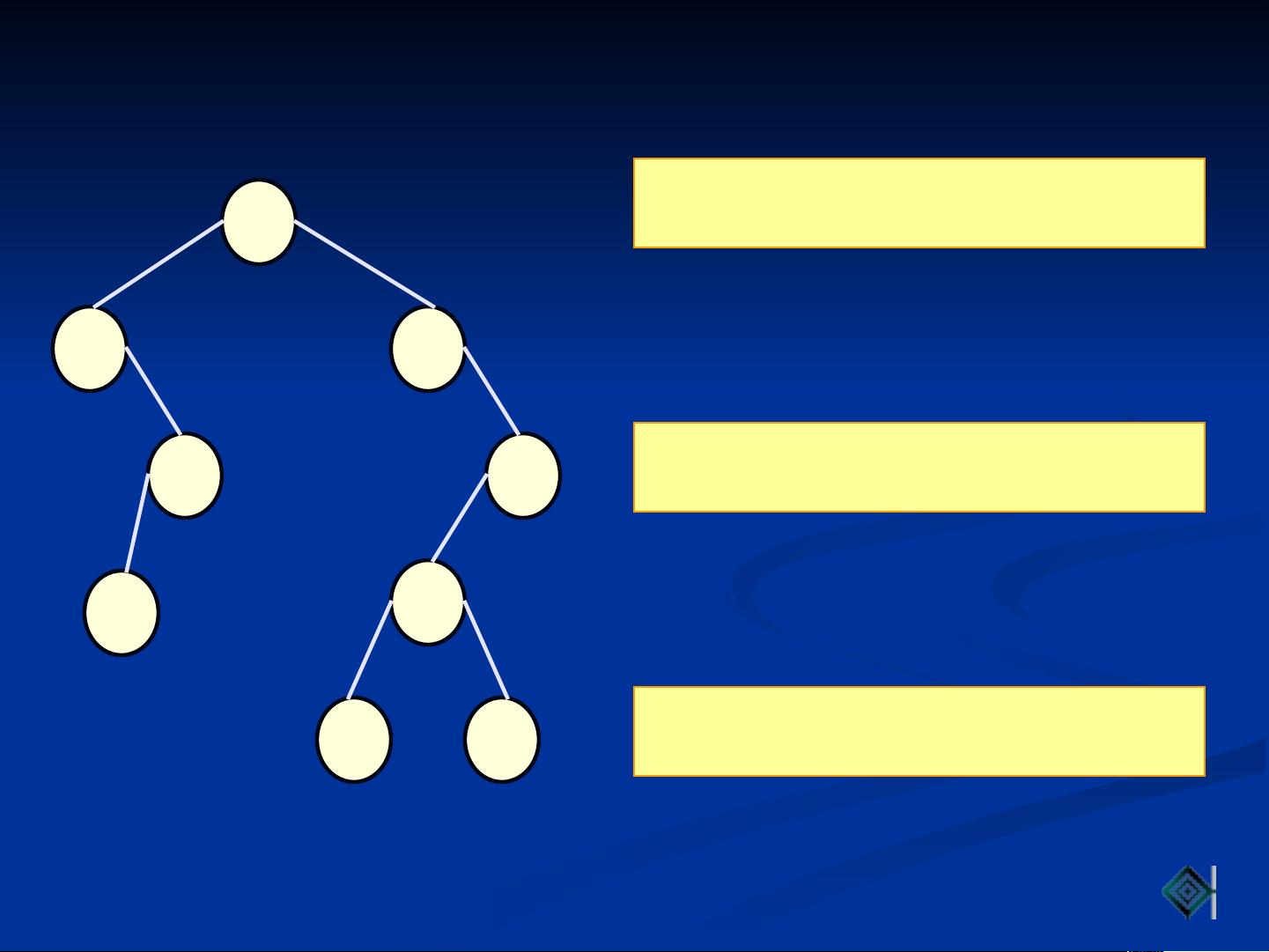
"本资源主要讲述了树和二叉树在算法中的应用，特别是关于树的生成和遍历。内容涵盖了二叉树的三种遍历方法：先序遍历、中序遍历和后序遍历，并提供了非递归和递归算法的实现。" 树和二叉树是数据结构中的基本概念，它们在计算机科学中有着广泛的应用，例如文件系统、编译器设计、图形算法等。二叉树是一种特殊的树形结构，每个节点最多有两个子节点，分为左子节点和右子节点。这种结构使得二叉树的操作效率较高，尤其是对于查找、插入和删除等操作。 **遍历二叉树**是理解其结构和数据的关键步骤。遍历是指按照特定顺序访问二叉树的所有节点，确保每个节点被访问且仅被访问一次。常见的遍历方法有以下三种： 1. **先序遍历（Preorder Traversal）**：首先访问根节点，然后遍历左子树，最后遍历右子树。用符号表示为：DLR（根-左-右）。 2. **中序遍历（Inorder Traversal）**：首先遍历左子树，然后访问根节点，最后遍历右子树。用符号表示为：LDR（左-根-右）。 3. **后序遍历（Postorder Traversal）**：首先遍历左子树，然后遍历右子树，最后访问根节点。用符号表示为：LRD（左-右-根）。 非递归算法通常使用栈来实现，通过对节点的压入和弹出控制遍历顺序。递归算法则直接利用函数调用自身，根据遍历顺序调用左右子树的遍历函数。 **先序遍历的递归算法**如下： ```c void Preorder(BiTree T) { if (T) { printf(T->data); // 访问结点 Preorder(T->lchild, visit); // 遍历左子树 Preorder(T->rchild, visit); // 遍历右子树 } } ``` **中序遍历的递归算法**如下： ```c void Inorder(BiTree T) { if (T) { Inorder(T->lchild, visit); // 遍历左子树 printf(T->data); // 访问结点 Inorder(T->rchild, visit); // 遍历右子树 } } ``` **后序遍历的递归算法**如下： ```c void Postorder(BiTree T) { if (T) { Postorder(T->lchild, visit); // 遍历左子树 Postorder(T->rchild, visit); // 遍历右子树 printf(T->data); // 访问结点 } } ``` 遍历二叉树的应用非常广泛，例如在构建表达式树、求解前缀、中缀和后缀表达式、构建哈夫曼树（用于数据压缩）以及计算树的深度和宽度等。通过遍历，我们可以将二叉树转换为不同的序列，这些序列可用于序列化和反序列化二叉树，或者用于算法的分析和设计。 总结来说，理解和掌握树和二叉树的遍历是学习数据结构和算法的重要部分，它为解决实际问题提供了基础工具。无论是非递归还是递归方式，遍历二叉树都是理解和操作这些数据结构的关键技能。