挖掘高价值模式：理论、算法与应用指南

需积分: 18 17 浏览量更新于2024-07-17 收藏 12.31MB PDF 举报

《高效实用模式挖掘：理论、算法与应用》是一本专著，收录在"Studies in Big Data"系列第51卷中，由Philippe Fournier-Viger、Jerry Chun-Wei Lin、Roger Nkambou、Bay Vo和Vincent S. Tseng共同编辑。本书于2019年1月19日首次出版，是针对大数据背景下高重要性模式（即高效实用模式）发现的深入研究。高效实用模式挖掘关注的是具有高价值或频繁度的项集和序列模式，对于商业智能、市场分析等领域具有重要意义。该书共分为十二章，其中七章是对高效率模式挖掘主要子领域的概述，包括： 1. 项集挖掘：研究数据集中频繁出现的项目组合。 2. 序列模式挖掘：处理时间序列数据中的模式发现。 3. 大数据模式挖掘：针对大规模数据集的高效算法和方法。 4. 元启发式方法：利用启发式策略优化模式挖掘过程。 5. 隐私保护模式挖掘：兼顾数据隐私和模式分析之间的平衡。 6. 模式可视化：通过图表展示复杂模式，便于理解和解释。另外五章则聚焦于关键技术和应用，如： - 发现简洁表示法：用更精炼的形式表达模式。 - 规则和结构化模式：揭示数据中的潜在规律和结构。《高效实用模式挖掘》不仅涵盖了理论基础，还介绍了核心算法以及实际应用案例，包括客户交易数据分析和序列数据挖掘。书中提到的软件和研究机会反映了当前领域的发展趋势。作为"Studies in Big Data"系列的一部分，这本书旨在快速传播大数据领域的新进展，并促进工程、计算机科学、物理学、经济学和生命科学等领域的交叉融合。对于那些对数据挖掘、业务分析和大数据技术感兴趣的读者，这是一本不可或缺的参考书籍，可以帮助他们理解如何从海量数据中提取有价值的信息，以支持决策制定和优化业务流程。价格方面，该书标价为$159.99，体现了其专业深度和实用性。

A Survey of High Utility Itemset Mining 7

Table 5 The high utility itemsets for mi nut il = 25

Itemset Utility Itemset Utility Itemset Utility

{a, c} 28 {b, c, d} 34 {b, d, e} 36

{a, c, e} 31 {b, c, d, e} 40 {b, e} 31

{a, b, c, d, e} 25 {b, c, e} 37 {c, e} 27

{b, c} 28 {b, d} 30

Table 6 The quantitative

transaction database

corresponding to the database

of Table1

TID Transaction

(a, 1), (b, 1), (c, 1), (d, 1), (e, 1)

(b, 1), (c, 1), (d, 1), (e, 1)

(a, 1), (c, 1), (d, 1)

(a, 1), (c, 1), (e, 1)

(b, 1), (c, 1), (e, 1)

Table 7 External utility

values for the database of

Table 6

Item External utility

a 1

b 1

c 1

d 1

e 1

discovering high utility itemsets can also be used to discover frequent itemsets in a

transaction database. To do that, the following steps can be applied:

1. The transaction database is converted to a quantitative transaction database. For

each item i ∈ I , the external utility value of i issetto1,thatis p(i) = 1 (to indicate

that all items are equally important). Moreover, for each item i and transaction

,ifi ∈ T

,setq(i, T

) = 1. Otherwise, set q(i, T

) = 0.

2. Then a high utility mining algorithm is applied on the resulting quantitative trans-

action database with mi nut il set to mi nsup, to obtain the frequent itemsets.

For example, the database of Table 1 can be transformed in a quantitative database.

The result is the transaction database of Tables 6 and 7. Then, frequent itemsets can

be mined from this database using a high utility itemset mining algorithm. How-

ever, although a high utility itemset mining algorithm can be used to mine frequent

itemsets, it may be preferable to use frequent itemset mining algorithms when per-

formance is important as these latter are optimized for this task.

8 P. Fournier-Viger et al.

2.3 Key Properties of the Problem of High Utility Itemset

Mining

For a given quantitative database and minimum utility threshold, the problem of high

utility itemset mining always has a single solution. It is to enumerate all patterns that

have a utility greater than or equal to the user-speciﬁed minimum utility threshold.

The problem of high utility itemset mining is difﬁcult for two main reasons. The

ﬁrst reason is that the number of itemsets to be considered can be very large to ﬁnd

those that have a high utility. Generally, if a database contains m distinct items there

are 2

− 1 possible itemsets (excluding the empty set). For example, if I ={a, b, c},

the possible itemsets are {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, and {a, b, c }. Thus, t here

are 2

− 1 = 7 itemsets, which can be formed with I ={a, b, c}. A naive approach

to solve the problem of high utility itemset mining is to count the utilities of all

possible itemsets by scanning the database, to then keep the high utility itemsets.

Although this approach produces the correct result, it is inefﬁcient. The reason is

that the number of possible itemsets can be very large. For example, if a retail store

has 10,000 items on its shelves (m = 10, 000), the utilities of 2

10,000

− 1 possible

itemsets should be calculated, which is unmanageable using the naive approach. It is

to be noted that the problem of high utility itemset mining can be very difﬁcult even

for small databases. For example, a database containing a single transaction of 100

items can produce 2

100

− 1 possible itemsets. Thus, the size of the search space (the

number of possible itemsets) can be very large even if there are few transactions in

a database. In fact, the size of the search space does not only depend on the size of

the database, but also on how similar the transactions are in the database, how large

the utility values are, and also on how low the mi nut il threshold is set by the user.

A second reason why the problem of high utility itemset mining is difﬁcult is

that high utility itemsets are often scattered in the search space. Thus, many itemsets

must be considered by an algorithm before it can ﬁnd the actual high utility itemsets.

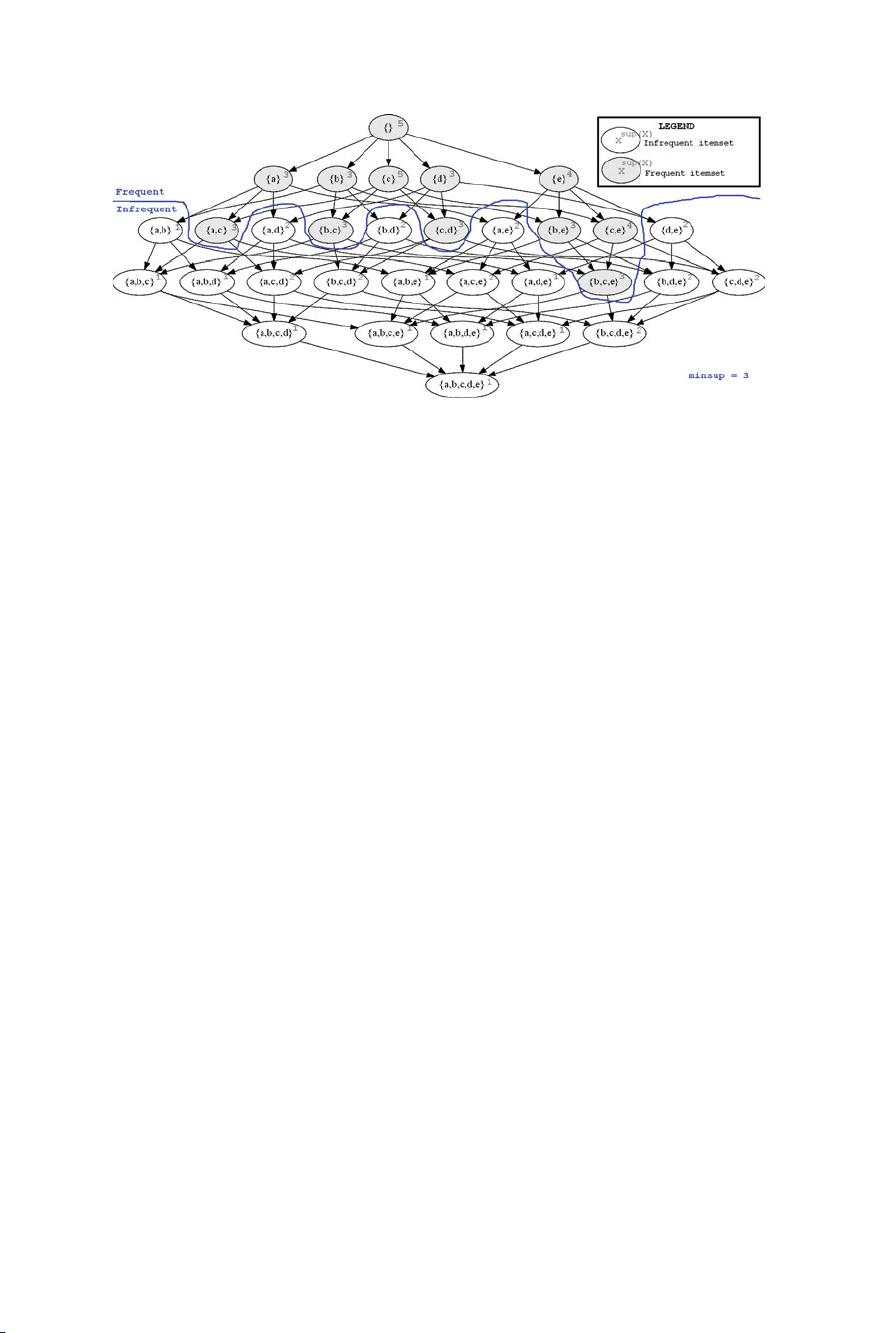
To illustrate this, Fig. 1 provides a visual representation of the search space for the

running example, as a Hasse diagram. A Hasse diagram is a graph where each

possible itemset is represented as a node, and an arrow is drawn from an itemset

X to another itemset Y if and only if X ⊆ Y and |X|+1 =|Y |.InFig.1,high

utility itemsets are depicted using light gray nodes, while low utility itemsets are

represented using white nodes. The utility value of each itemset is also indicated.

An important observation that can be made from that ﬁgure is t hat the utility of an

itemset can be greater, higher or equal, to the utility of any of its supersets/subsets.

For example, the utility of the itemset {b, c} is 28, while the utility of its supersets

{b, c, d} and {a, b, c, d, e} are 34 and 25, respectively. Formally, it is thus said that

the utility measure is neither monotone nor anti-monotone.

Property 1 (The utility measure is neither monotone nor anti-monotone) Let there

be two itemsets X and Y such that X ⊂ Y . The relationship between the utilities of

X and Y is either u(X)<u(Y ),u(X)>u(Y ),oru(X) = u(Y ) [83].

A Survey of High Utility Itemset Mining 9

Fig. 1 The search space of high utility itemset mining for the running example and mi nut il = 25

Because of this property, the high utility itemsets appear scattered in the search

space, as it can be observed in Fig. 1. This is the main reason why the problem of

high utility itemset mining is more difﬁcult than the problem of frequent itemset

mining [2]. In frequent itemset mining, the support measure has the nice property of

being monotone [2], that is, the support of an itemset is always greater than or equal

to the frequency of any of its supsersets.

Property 2 (The support measure is monotone) Let there be two itemsets X and Y

such that X ⊂ Y . It follows that sup(X ) ≥ su p(Y ) [2].

For example, in the database of Table 1, the support of {b, c} is 3, while the

support of its supersets {b, c, d} and {a, b, c, d, e} are 2 and 1, respectively. The

monotonicity of the support measure makes it easy to ﬁnd frequent patterns as it

guarantees that all supersets of an infrequent itemset are also infrequent [2]. Thus, a

frequent itemset mining algorithm can discard all supersets of an infrequent itemset

from the search space. For example, if an algorithm ﬁnds that the itemset {a, d} is

infrequent, it can directly eliminate all supersets of {a, d} from further exploration,

thus greatly reducing the search space. The search space for the example database

of Table 1 is illustrated in Fig. 2. The anti-monotonicity of the support can be clearly

observed in this picture as a line is drawn that clearly separates frequent itemsets

from infrequent itemsets. Property 2 is also called the downward-closure property,

anti-monotonicity-property or Apriori-property [2]. Although it holds for the support

measure, it does not hold for the utility measure used in high utility itemset mining.

As a result, in Fig. 1, it is not possible to draw a clear line to separate low utility

itemsets from high utility itemsets.

Due to the large search space in high utility itemset mining, it is thus important to

design fast algorithms that can avoid considering all possible itemsets in the search

space and that process each itemset in the search space as efﬁciently as possible,

while still ﬁnding all high utility itemsets. Moreover, because the utility measure is

not monotone nor anti-monotone, efﬁcient strategies for reducing the search space

used in frequent itemset mining cannot be directly used to solve the problem of high

10 P. Fournier-Viger et al.

Fig. 2 The search space of frequent itemset mining for the database of Table 1 and mi nsu p = 3

utility itemset mining. The next section explains the key ideas used by the state-of-

the-art high utility itemset mining algorithms to solve the problem efﬁciently.

3 Algorithms

Several high utility itemset mining algorithms have been proposed such as UMin-

ing [82], Two-Phase [59], IHUP [5], UP-Growth [79], HUP-Growth [52], MU-

Growth [87], HUI-Miner [58], FHM [31], ULB-Miner [17], HUI-Miner* [71] and

EFIM [94]. All of these algorithms have the same input and the same output. The

differences between these algorithms lies in t he data structures and strategies that are

employed for searching high utility itemsets. More speciﬁcally, algorithms differ in

(1) whether they use a depth-ﬁrst or breadth-ﬁrst search, (2) the type of database rep-

resentation that they use internally or externally, (3) how they generate or determine

the next itemsets to be explored in the search space, and (4) how they compute the

utility of itemsets to determine if they satisfy the minimum utility constraint. These

design choices inﬂuence the performance of these algorithms in terms of execution

time, memory usage and scalability, and also how easily these algorithms can be

implemented and extended for other data mining tasks. Generally, all high utility

itemset mining algorithms are inspired by classical frequent itemset mining algo-

rithms, although they also introduce novel ideas to cope with the fact that the utility

measure is neither monotone nor anti-monotone.

Early algorithms for the problem of high utility itemset mining were incomplete

algorithms that could not ﬁnd he complete set of high utility itemsets due to the use

of heuristic strategies to reduce the search space. For example, this is the case of

the UMining and UMining_H algorithms [82]. In the rest of this section, complete

algorithms are reviewed, which guarantees to ﬁnd all high utility itemsets. It is also

interesting to note that the term high utility itemset mining has been ﬁrst used in

2003 [11], although the problem deﬁnition used by most researchers nowadays, and

used in this chapter, has been proposed in 2005 [83].

A Survey of High Utility Itemset Mining 11

3.1 Two Phase Algorithms

The ﬁrst complete algorithms to ﬁnd high utility itemsets perform two phases, and

are thus said to be two phase algorithms. This includes algorithms such as Two-

Phase [59], IHUP [5], UP-Growth [79], HUP-Growth [52], and MU-Growth [87].

The breakthrough idea that has inspired all these algorithms was introduced in Two-

Phase [59]. It is that it is possible to deﬁne a monotone measure that is an upper-bound

on the utility measure, and to use that measure to safely reduce the search space

without missing any high utility itemsets. The measure proposed in the Two-Phase

algorithm i s the TWU (Transaction Weighted Utilization) measure, which is deﬁned

as follows:

Deﬁnition 7 (The TWU measure)Thetransaction utility (TU) of a transaction T

is the sum of the utilities of all the items in T

. i.e. TU(T

) =



x∈T

u(x, T

).The

transaction-weighted utilization (TWU) of an itemset X is deﬁned as the sum of the

transaction utilities of transactions containing X , i.e. TWU(X ) =



∈g(X)

TU(T

For instance, the transaction utilities of T

, T

and T

are respectively 25,

20, 8, 22 and 9. The TWU of single items a, b, c, d, e are respectively 55, 54, 84,

53 and 76. The TWU of the itemset {c, d} is TWU({c, d}) = TU(T

) + TU(T

) +

TU(T

) = 25 + 20 + 8 = 53. The TWU measure is said to be an upper-bound on

the utility measure that is monotone. This idea is formalized as the next property.

Property 3 (The TWU is a monotone upper-bound on the utility measure) Let

there be an itemset X . The TWU of X is no less than its utility (T W U (X) ≥ u(X)).

Moreover, the TWU of X is no less than the utility of its supersets (T W U(X) ≥

u(Y )∀Y ⊃ X). The proof is provided in [59]. Intuitively, since the TWU of X is the

sum of the utility of transactions where X appears, its TWU must be greater or equal

to the utility of X and any of its supersets.

The TWU measure is interesting because it can be used to reduce the search space.

For this purpose, the following property was proposed.

Property 4 (Pruning the search space using the TWU) For any itemset X , if

TWU(X)<minutil, then X is a low-utility itemset as well as all its supersets.

This directly follows from Property3.

For example, the utility of the itemset {a, b, c, d} is 20, and TWU({a, b, c, d}) =

25. Thus, by t he Property 4, it is known that any supersets of {a, b, c, d} cannot have

a TWU and a utility greater than 25. As a result, if the user sets the mi nuti l threshold

to a value greater than 25, all supsersets of {a, b, c,

d} can be eliminated from the

search space as it is known by Property 4 that their utilities cannot be greater than

25.

Algorithms such as IHUP [5], PB [47], Two-Phase [59], UP-Growth [79], HUP-

Growth [52] and MU-Growth [87] utilize Property 4 as main property to prune the

search space. They operate in two phases:

剩余342页未读，继续阅读

THESUMMERE

粉丝: 23
资源: 328

挖掘高价值模式：理论、算法与应用指南

pyannote.algorithms-0.7-py3-none-any.whl：Python库的官方压缩包

Javascript-Algorithms示例教程：掌握Shellsort算法

"ISO/IEC-13818-7-2006: AAC音频编码标准详解

high-performance-data-mining-scaling-algorithms-applications-and-systems

Two-dimensional Phase Unwrapping: Theory, Algorithms, and Software的源代码

Two-dimensional phase unwrapping: theory, algorithms, and software 书籍中的代码

（part3）Two-dimensional phase unwrapping: theory, algorithms, and software3

Fast algorithms for hiding sensitive high-utility itemsets in privacy-preserving utility mining

leetcode答案-MIT-6.006-Introduction-to-Algorithms:https://ocw.mit.edu/cou

javascript-data-structures-and-algorithms：练习，算法

最新资源