四元数与三维旋转的理解与应用

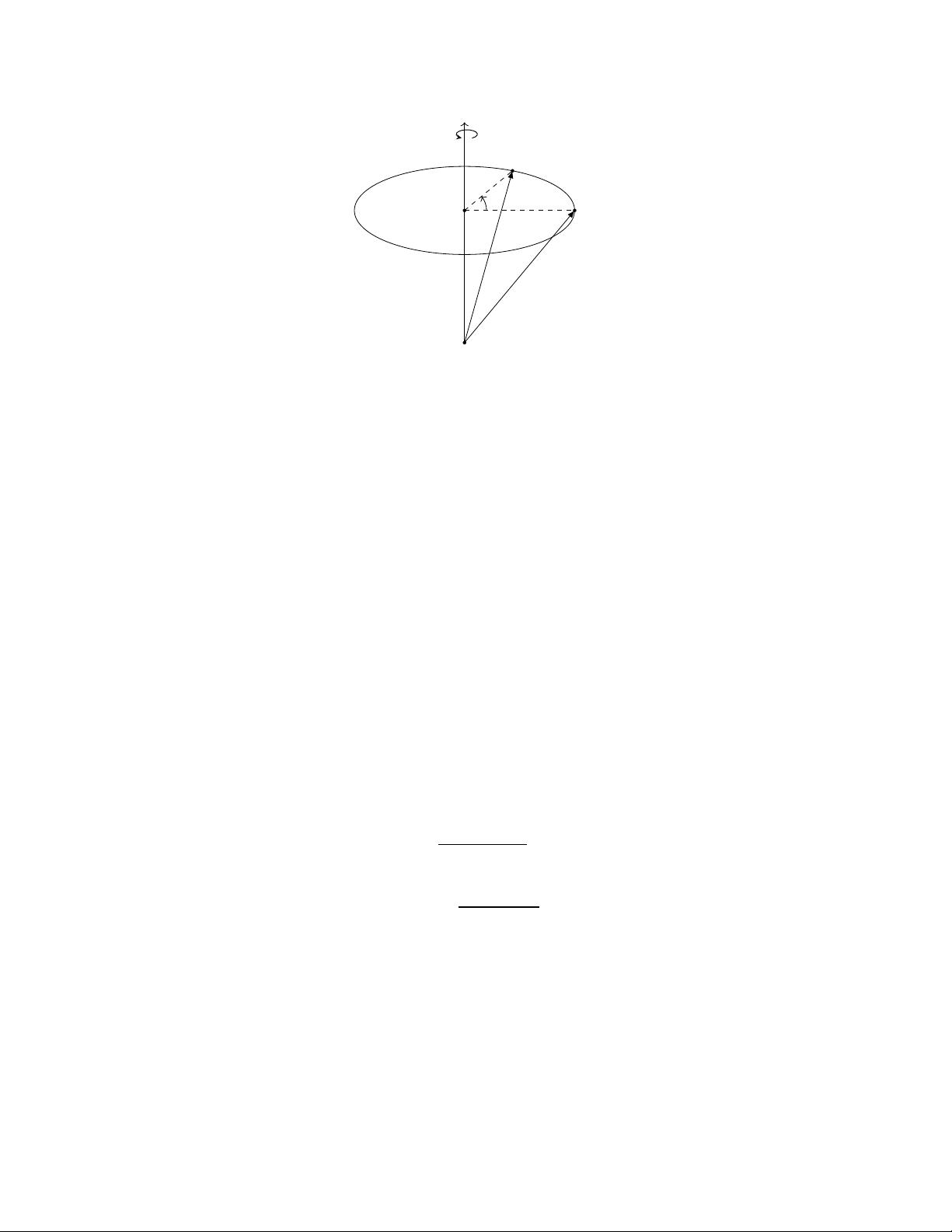
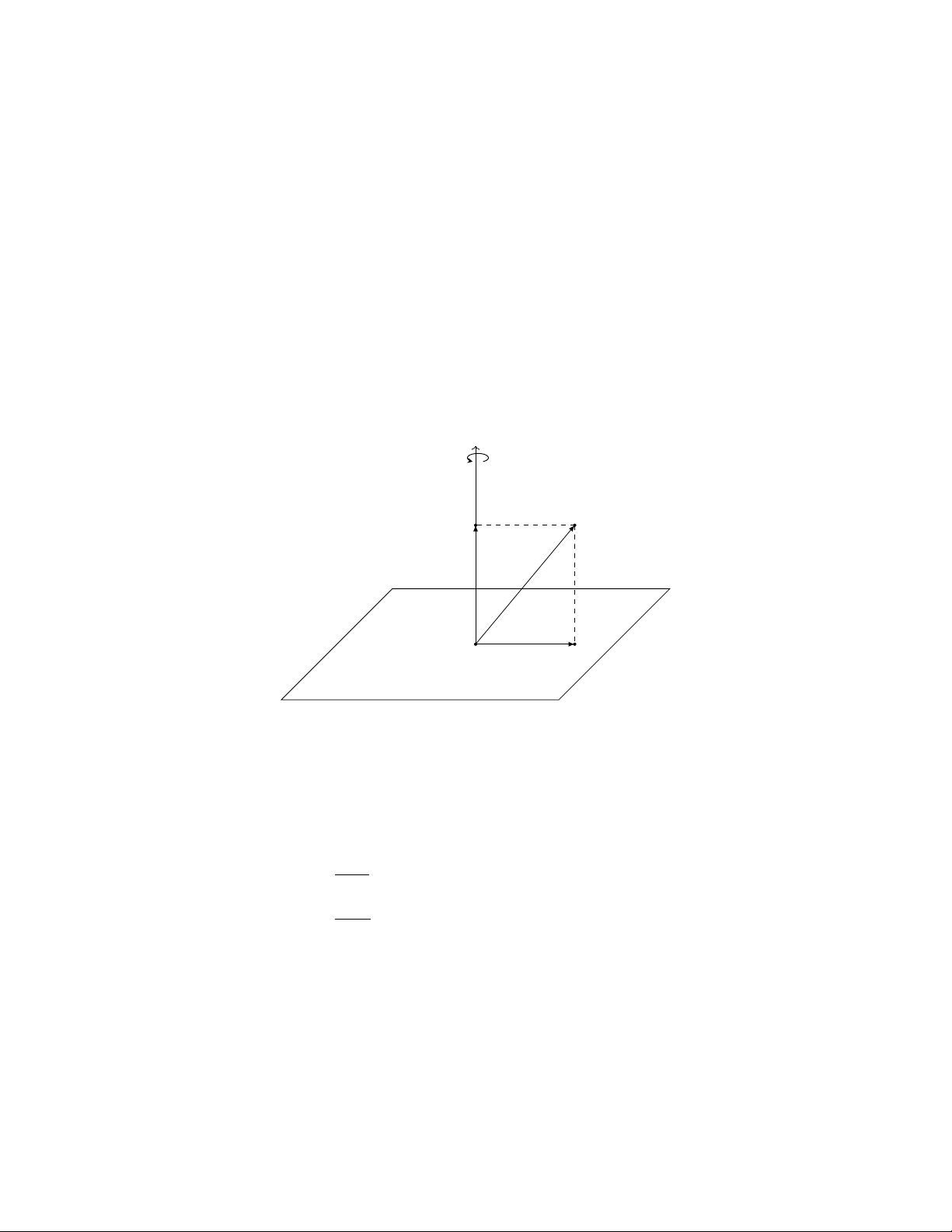
"该资源是一篇关于四元数及其在三维旋转中应用的文章，作者通过简单易懂的方式探讨四元数与3D旋转的关系，使用几何学和线性代数的知识进行推导。文章适合对3D图形学感兴趣的人群，同时也提供了一些MATLAB/Octave的代码示例和相关动画。文章遵循'CCBY-NC-SA4.0'协议发布。" 文章首先介绍了复数的概念，作为理解四元数的基础。复数由实部和虚部组成，可以视为二维空间中的向量。复数的乘法运算结合了欧几里得几何中的旋转，其中i² = -1，这使得复数能够表示2D平面上的旋转。 接下来，文章引出了四元数，它是复数的扩展，用于处理三维空间中的旋转。四元数由一个实部和三个虚部构成，可以表示为q = w + xi + yj + zk，其中w, x, y, z ∈ R，i, j, k是四元数的基，满足i² = j² = k² = ijk = -1。这种表示允许四元数描述三维空间中的旋转而不引入旋转向量的问题，如万向节死锁。 四元数的乘法规则使得它们能够自然地表示角度和轴的旋转。一个单位四元数（模长为1的四元数）可以表示一个旋转，其实部w对应于旋转角的余弦值，虚部(x, y, z)对应于旋转轴上的单位向量。通过四元数乘法，可以轻松地组合多个旋转，这是3D图形学和游戏开发中常用的方法。 文章还指出，相比于矩阵旋转，四元数更加紧凑且计算效率更高，特别是在处理大量旋转时。它们还可以避免使用旋转矩阵可能导致的奇异性和不稳定性。 在实际应用中，四元数常用于3D图形渲染、模拟和姿态控制等领域。作者提供了MATLAB/Octave的代码和动画，帮助读者直观地理解四元数如何表示和执行三维旋转。 最后，文章提到了一些更抽象的内容，包括四元数的代数结构和与群论的联系，但这些不是文章的重点。作者建议对物理学或抽象代数感兴趣的人可以参考扩展阅读材料。 这篇文章是学习四元数及其在三维旋转应用的一个良好起点，尤其适合具有基本线性代数知识的读者。通过深入理解四元数，读者能够更好地掌握3D空间中的旋转表示和计算。