"深入理解计算机图形学中的光栅化算法与反走样技术"

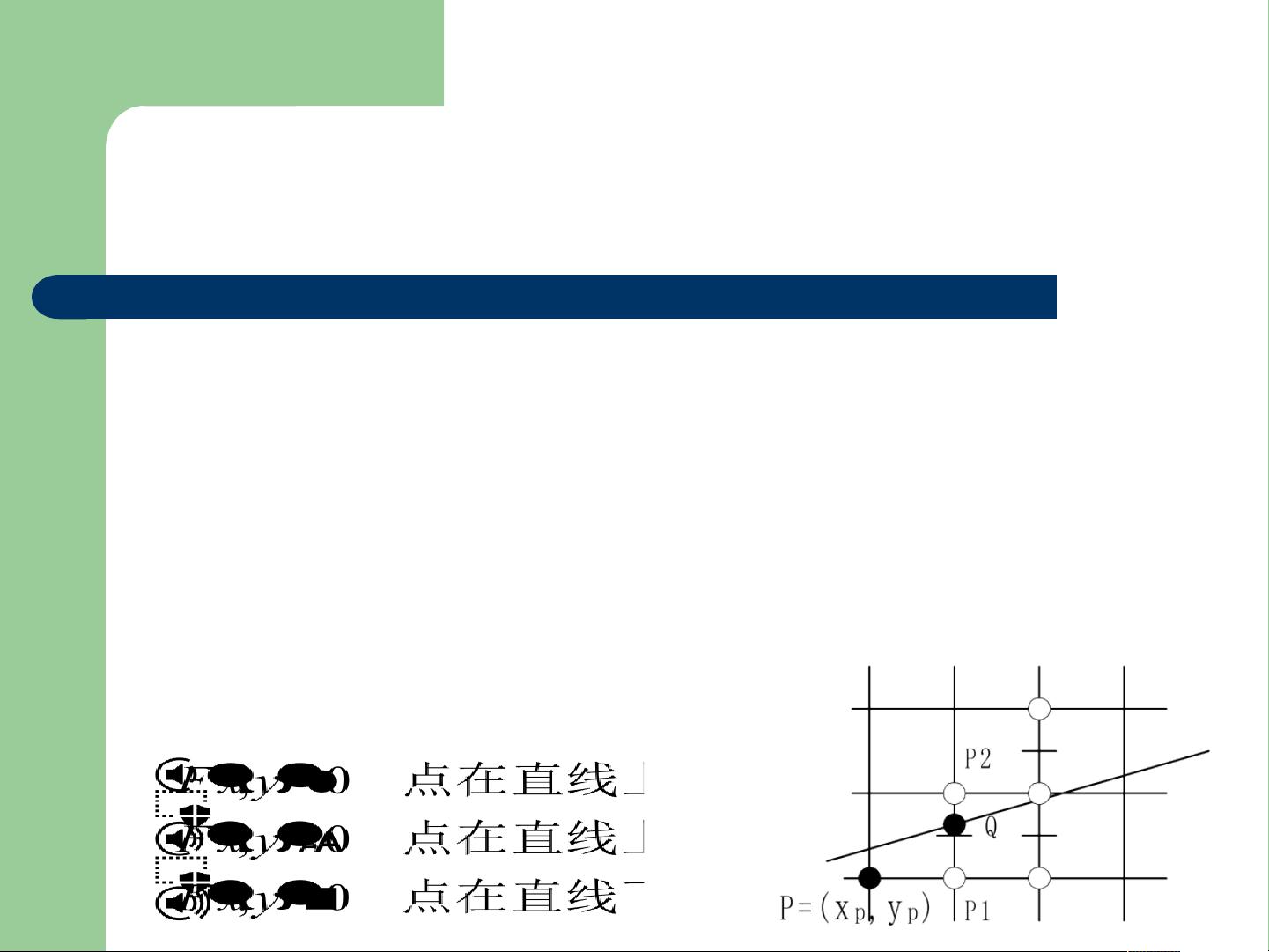
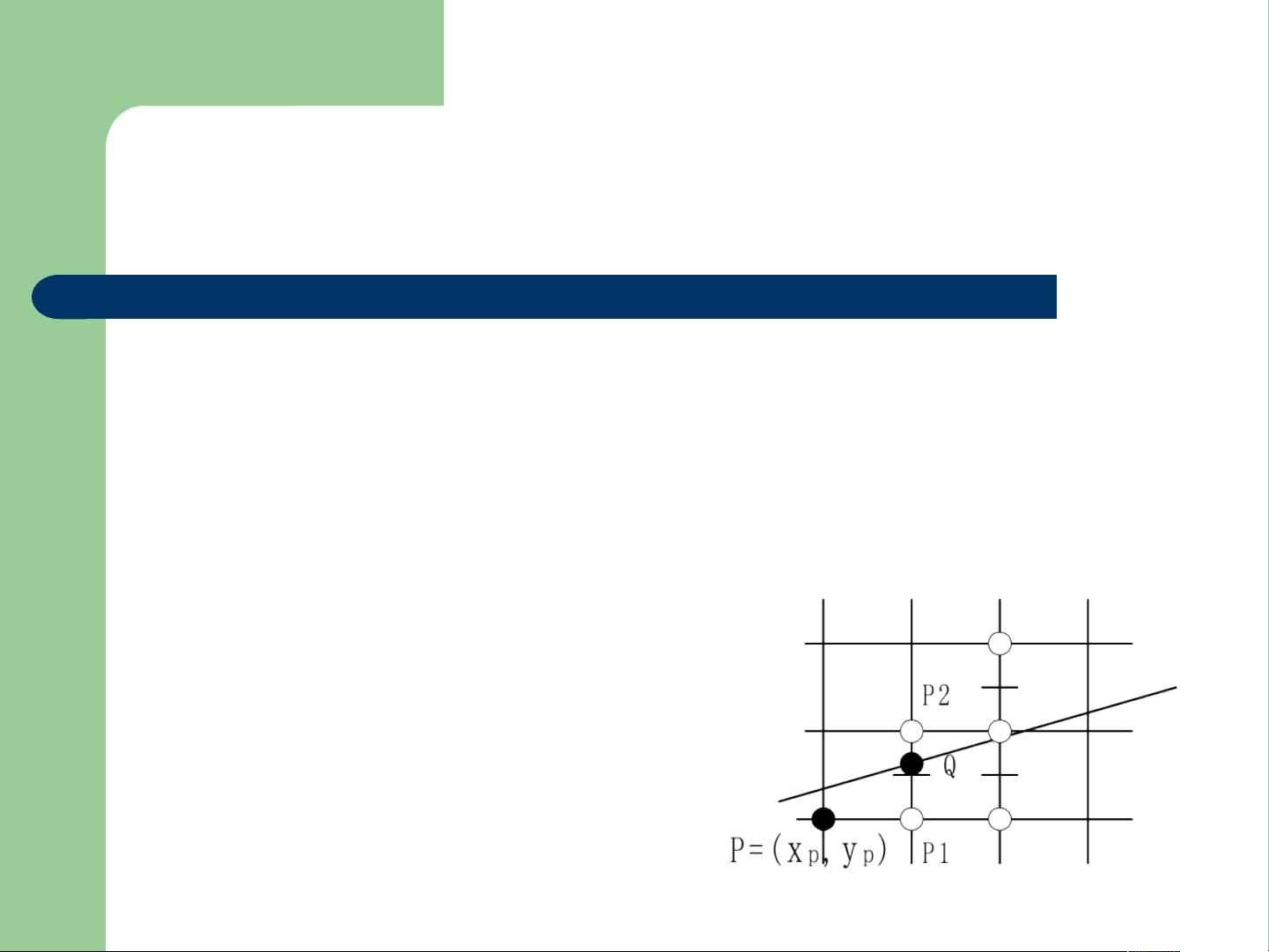
计算机图形学是研究如何利用计算机生成、处理和显示图形的学科。在计算机图形学的学习过程中，光栅图形学是一个重要的章节。光栅图形学涉及到直线段的扫描转换算法、圆弧的扫描转换算法、多边形的扫描转换与区域填充、字符、裁剪、反走样以及消隐等内容。 在直线段的扫描转换算法中，有三种常用的算法：数值微分法（DDA算法）、中点画线法和Bresenham画线算法。数值微分法的基本思想是通过给定直线的起点和终点的坐标，计算出直线上各点的坐标。算法通过计算出每个x方向上的增量，根据直线的斜率计算出相应的y坐标。中点画线法是一种更高效的算法，通过利用直线的斜率和中点的位置来确定下一个像素的位置。Bresenham画线算法是一种更为精确和高效的算法，通过利用整数运算来实现直线的绘制。 圆弧的扫描转换算法包括了对圆弧的绘制以及圆弧的填充。对于圆弧的绘制，常用的算法有三种：中点圆弧生成算法、中点椭圆生成算法和Bresenham圆生成算法。这些算法通过计算出圆弧上各个点的坐标，实现了圆弧的绘制。对于圆弧的填充，通常使用扫描线填充算法，该算法通过扫描线的方式将圆弧的内部区域进行填充。 多边形的扫描转换与区域填充是计算机图形学中常用的算法之一。多边形的扫描转换算法主要是通过划分成多个三角形来进行绘制。区域填充算法则是通过填充多边形内部的像素来实现填充效果。常见的算法有扫描线填充算法、种子填充算法等。 字符的绘制是计算机图形学中的一个重要应用场景。在计算机图形学中，通常通过预先设计好的字库来实现字符的绘制。绘制字符的算法主要涉及到字符的坐标定位和像素值的计算。 裁剪是计算机图形学中实现图形显示的一项必要技术。常用的裁剪算法有线段裁剪算法和多边形裁剪算法。线段裁剪算法主要包括Cohen-Sutherland算法和Liang-Barsky算法。多边形裁剪算法主要包括CSG算法和Weiler-Atherton算法。 反走样是图形学中常用的一种技术，用于解决图形在显示过程中产生的锯齿和像素化问题。常用的算法有超级采样和多级采样等。 消隐是计算机图形学中实现真实感觉的一项重要技术。消隐算法主要包括深度缓冲消隐算法、扫描线Z缓冲算法和后向面消隐算法等。 在学习计算机图形学的过程中，需要掌握光栅图形学中的各种扫描转换算法，并能够理解和实现这些算法的原理。光栅图形学是计算机图形学的基础，对于理解和掌握其他高级图形学技术也具有重要作用。