小波分解与重构：理论与MATLAB实现

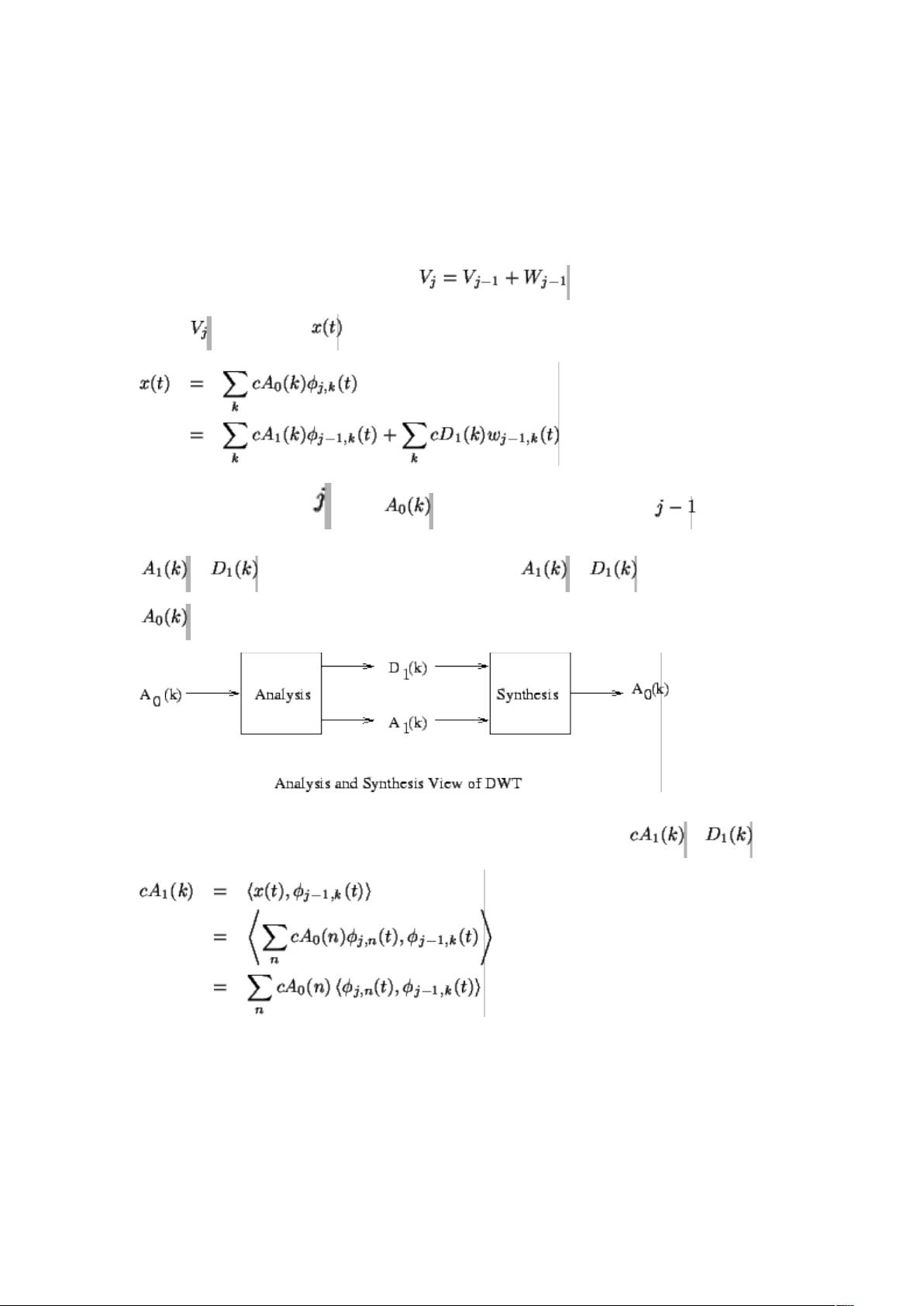
"该资源主要介绍了信号的小波分解与重构原理，并提供了MATLAB程序作为参考。文档涉及到离散小波变换(DWT)的理论，以及如何通过滤波器组实现小波分解和重构。同时，通过一个组合正弦信号的例子展示了小波分解的过程。" 小波分解与重构是数字信号处理中的重要技术，它利用小波函数的多分辨率分析特性对信号进行分析和重构。在离散小波变换中，信号可以被表示为不同尺度和位置的小波基函数的线性组合，这使得我们能够分别在不同时间-频率局部化区域内研究信号的特征。 1. **小波分解原理**： - 在离散小波变换中，信号[pic]可以在尺度度量空间[pic]上通过一组基函数进行表示，这些基函数通常由小波母函数生成的不同尺度和位置的版本组成。 - 分解过程涉及两个关键步骤：低通滤波（对应于低频或细节信息）和高通滤波（对应于高频或边缘信息）。这可以通过一对滤波器（通常是小波滤波器组）来实现，即分析滤波器（h0, h1）和重构滤波器（g0, g1）。 - 系数[pic]和[pic]分别代表了在不同尺度下的信号信息，通过内积公式可以计算得到。 2. **小波重构原理**： - 重构过程是分解的逆操作，通过已知的系数[pic]和[pic]，结合重构滤波器恢复原始信号。 - 这个过程通常涉及多次卷积操作，将低频部分和高频部分的系数分别通过相应的重构滤波器，然后合并得到重构信号。 3. **具体实现**： - 示例中，使用了一个组合正弦信号，包含了三个不同频率的正弦波。通过MATLAB程序展示了如何使用滤波器组进行小波分解。 - 分解过程包括使用h0和h1滤波器对原始信号进行卷积，提取出低频成分（a0, a1）和高频成分（w0, w1）。 - 分解结果通过傅里叶变换展示其频域特性，进一步验证了分解的有效性。 4. **应用意义**： - 小波分解和重构在图像处理、声音分析、故障诊断、数据压缩等领域有广泛应用，因为它能够提供信号在不同时间和频率尺度上的详细信息。 小波分解与重构是信号处理中的一种强大工具，它能够捕捉到信号的局部特征，特别是在非平稳信号分析中，小波变换的优势尤为突出。通过理解这一原理并结合MATLAB程序，可以深入学习和应用小波理论解决实际问题。