线性规划与优化：从基础到网络流和二分图匹配

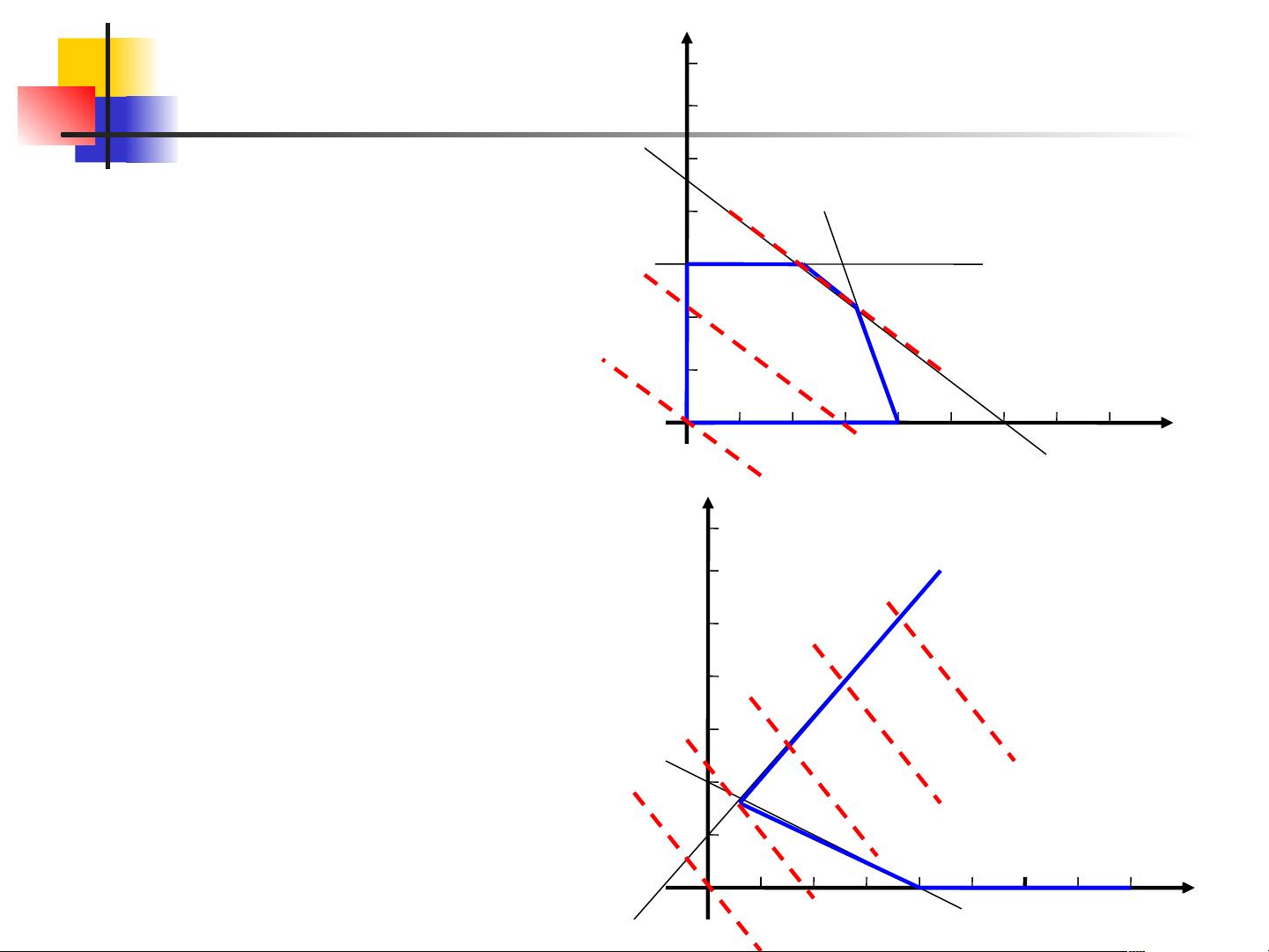
"该资源详细介绍了线性规划、网络流和二分图匹配这三个重要的算法概念，并通过实例进行解析。" 线性规划是一种优化技术，用于在满足一系列线性约束条件下最大化或最小化一个线性目标函数。在给定的例子中，目标是最大化利润（Z），而利润由产品X1和X2的产量决定。约束条件限制了产量的可能性，比如生产能力的限制。线性规划的问题可以表示为以下形式： max Z = c1x1 + c2x2 + ... + cnxn s.t. a11x1 + a12x2 + ... + a1nxn ≤ b1 a21x1 + a22x2 + ... + a2nxn ≤ b2 ... am1x1 + am2x2 + ... + amnxn ≤ bm 其中，x1, x2, ..., xn 是决策变量，c1, c2, ..., cn 是对应变量的目标函数系数（表示每个变量对目标函数的影响），aij 和 bi 是约束条件的系数和右边的常数。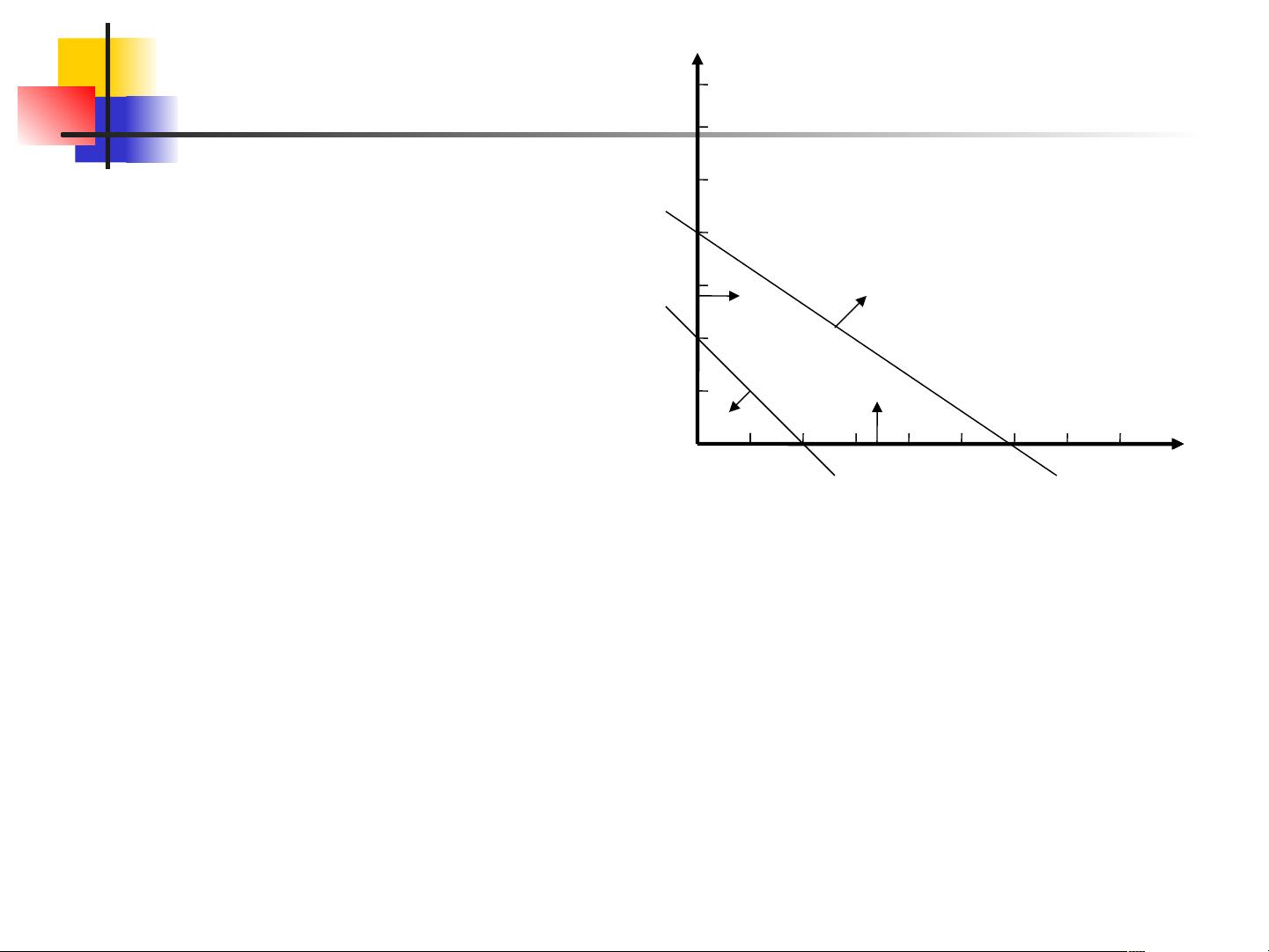 线性规划的解可以分为四种情况：唯一解、无穷多解、无界解和无可行解。当可行域是有界的凸多边形时，最优解总是出现在凸集的一个顶点，可以通过比较不同顶点的目标函数值来找到这个最优解。如果可行域是无界的，可能存在无穷多最优解或无界解。如果没有任何解满足约束条件，那么问题就无可行解，也就没有最优解。 在解决线性规划问题时，常用的方法有图解法和单纯形法。图解法适用于只有两个变量的情况，可以通过绘制二维图形来寻找解。而单纯形法则适用于任意数量的变量，它是一种迭代方法，通过不断调整变量的值，逐步接近最优解。 网络流问题是在网络结构中，研究如何从源点向汇点有效地分配资源，使得总流量达到最大或者满足某些特定条件。常见的网络流问题有最大流问题和最小割问题，它们在物流、通信网络等领域有广泛应用。 二分图匹配则是图论中的一个概念，涉及到在一个图中找到尽可能多的相互独立的边，这些边的端点分别来自图的两部分。二分图匹配在配对问题、任务分配等实际场景中有重要应用，如稳定婚姻问题和霍夫曼编码等。 线性规划、网络流和二分图匹配都是运筹学和图论中的基础工具，它们在优化问题的解决中扮演着核心角色，广泛应用于工程、经济、计算机科学等多个领域。理解并掌握这些理论知识，对于解决实际问题具有很高的价值。