动态规划解决旅行路线问题 - 无后效性原则解析

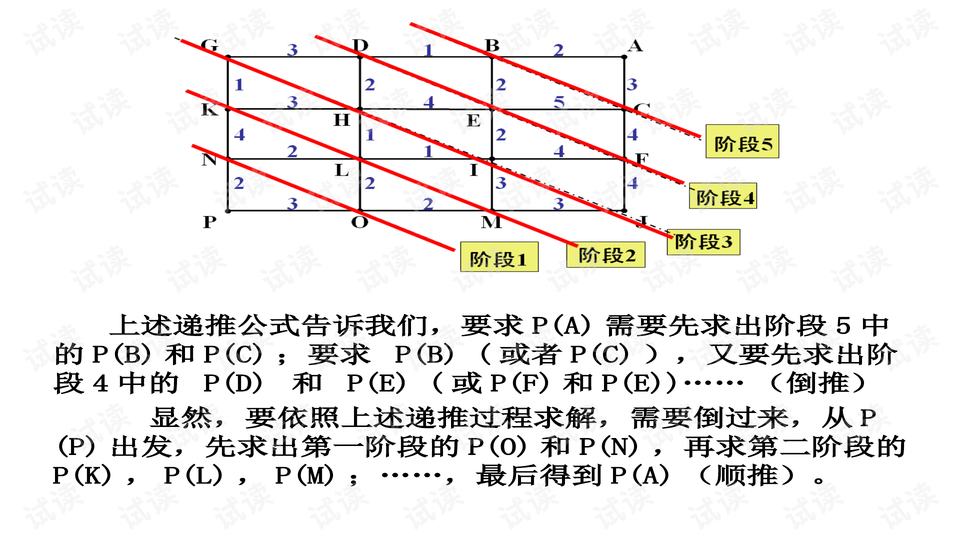
"旅行路线问题满足“无后效性原则”的动态规划讲解，涉及NOIP竞赛相关知识，包括动态规划的基本概念、基础题型和综合题型。" 在这篇讲稿中，主要讨论的是如何利用动态规划解决旅行路线问题，这个问题符合"无后效性原则"，即一旦做出某个阶段的决策，对之前阶段的决策就不再产生影响。这种特性使得动态规划成为解决问题的理想工具。 首先，我们来看动态规划的基本概念。动态规划是一种用于解决多阶段决策问题的优化方法，其核心在于通过分阶段进行决策，并确保每一阶段的决策最优，从而达到整体最优。在这个过程中，状态的变化是由每个阶段的决策引起的，且每个阶段的决策会影响到后续阶段的状态。 具体到旅行路线问题，我们可以将其分为两条航线，分别是从东到西的路径。定义阶段为[P1, P2]，表示第一条航线到达城市P1，第二条航线到达城市P2。如果阶段[P1, P2]可以到达阶段[Q1, Q2]，则必须满足P1<Q1或P2<Q2，确保旅行路线始终由左向右推进。例如，阶段[3, 4]可以通过增加边(4, 5)转换为阶段[3, 5]，但不能从[3, 5]返回到[3, 4]，因为这违反了旅行的顺序要求。 动态规划的求解通常采用自底向上的方式，即从最基础的阶段开始逐步构建到目标阶段。在这个例子中，要计算阶段[i, j]经过的城市数，我们需要知道阶段[i, k]（或[k, j]）经过的城市数。通过递推关系，我们可以逐步解决这个问题。 讲稿中提到的二维数组h[4][3]存储了东西方向的道路长度，这表明问题的规模可能是4个城市横向排列，每个城市有3条东西向的出路。类似地，如果存在南北方向的道路，它们的长度可能存储在另一个数组中。使用这些数组，我们可以计算出任意两个城市之间的最短路径，从而找出满足条件的旅行路线。 总结来说，这篇讲稿深入浅出地介绍了动态规划的概念，并通过旅行路线问题实例阐述了如何应用动态规划解决实际问题。它涵盖了基础题型和综合题型，对于参加NOIP（全国青少年信息学奥林匹克联赛）的学生来说，是一个很好的学习资料，有助于理解和掌握动态规划的精髓。