《信号处理基础》Sophocles J. Orfanidis-数字信号处理概论

4星 · 超过85%的资源需积分: 37 18 浏览量更新于2024-07-26 收藏 6.8MB PDF 举报

"这是一本关于数字信号处理的英文原版书籍，由Sophocles J. Orfanidis撰写，适用于学习用途，包含13个章节的内容。作者授权于2010年，之前由Pearson Education, Inc.出版，首次出版时的ISBN号为0-13-209172-0。书中使用了MATLAB商标，并在Rutgers University的作者网页上可以找到更多相关信息。" 《Introduction to Signal Processing》由Sophocles J. Orfanidis教授撰写，是一部深入浅出介绍数字信号处理的经典教材。该书主要面向对信号处理感兴趣的读者，无论是初学者还是有一定基础的学者，都能从中受益。书中涵盖了一系列关键概念和技术，旨在帮助读者理解和应用信号处理的基本原理。第一章“Sampling and Reconstruction”是整个信号处理领域的基础，它探讨了将连续时间信号转换为离散时间信号（采样）以及如何从这些离散样本中恢复原始信号（重构）的过程。以下是本章的关键知识点： 1.1 引言：这部分介绍了信号处理的基本概念，阐述了为什么需要进行信号的采样和重构，以及在实际应用中的重要性。 1.2 模拟信号回顾：回顾了模拟信号的基本特性，包括频率、幅度和波形，为后续的采样理论铺垫基础。 1.3 采样定理：这是信号处理的核心理论，说明了为了无失真地重构一个模拟信号，采样频率至少应为信号最高频率的两倍，即奈奎斯特采样率。这部分还解释了过采样和欠采样的后果。 1.3.1 采样定理：详细阐述了采样定理的数学表述和物理意义，强调了避免混叠的重要性。 1.3.2 防混叠预滤波器：在采样前应用预滤波器来去除高于奈奎斯特频率的成分，防止信号混叠。 1.3.3 硬件限制：讨论了实际硬件设备在采样和重构过程中可能遇到的限制，如带宽、噪声和非理想滤波器的影响。 1.4 采样正弦波：通过具体例子展示如何对不同频率的正弦波进行采样，分析了采样过程中的行为。 1.4.1 模拟重构与混叠：解释了采样后重构模拟信号时可能出现的混叠现象，以及如何通过适当的处理避免它。 1.4.2 旋转运动：将信号采样与旋转运动类比，帮助读者直观理解采样过程中频率的变化。 1.4.3 数字信号处理频率单位：介绍了在数字信号处理中使用的频率单位，如数字频率和角频率，以及它们与模拟频率的关系。整个章节旨在通过理论讲解和实例分析，使读者掌握采样和重构的基本概念，为后续章节的学习打下坚实的基础。书中可能还涉及了滤波器设计、数字信号处理算法以及信号分析工具，如MATLAB的使用等。通过学习这本书，读者能够对数字信号处理有全面而深入的理解，从而在通信、图像处理、音频处理等领域应用这些知识。

1.4. SAMPLING OF SINUSOIDS 19

When we develop DFT algorithms, we will see that the aliased Fourier series coef-

ﬁcients for the above type of problem can be obtained by performing a DFT, provided

that the periodic analog signal remains a periodic discrete-time signal after sampling.

This requires that the sampling frequency

be an integral multiple of the fundamen-

tal harmonic of the given signal, that is,

= Nf

. In such a case, the aliased coefﬁcients

can be obtained by an

N-point DFT of the ﬁrst N time samples x(nT), n = 0, 1,...,N−1

of the analog signal. See Section 9.7.

Example 1.4.7:

A sound wave has the form:

x(t) = 2A cos(10πt)+2B cos(30πt)

2C cos(50πt)+2D cos(60πt)+2E cos(90πt)+2F cos(125πt)

where t is in milliseconds. What is the frequency content of this signal? Which parts of it

are audible and why?

This signal is preﬁltered by an analog preﬁlter

H(f). Then, the output y(t) of the pre-

ﬁlter is sampled at a rate of 40 kHz and immediately reconstructed by an ideal analog

reconstructor, resulting into the ﬁnal analog output

(t), as shown below:

prefilter

H(f)

40 kHz

sampler

analog

reconstructor

x(t)

y(t) y

(t)y(nT)

digitalanalog analog analog

Determine the output signals y(t) and y

(t) in the following cases:

(a) When there is no preﬁlter, that is,

H(f)= 1 for all f .

(b) When

H(f) is the ideal preﬁlter with cutoff f

/2 = 20 kHz.

H(f) is a practical preﬁlter with speciﬁcations as shown below:

20 40 60

60 dB/octave

(-60 dB)

(0 dB)

Analog Prefilter

80 kHz

H(f)

That is, it has a ﬂat passband over the 20 kHz audio range and drops monotonically

at a rate of 60 dB per octave beyond 20 kHz. Thus, at 40 kHz, which is an octave

away, the ﬁlter’s response will be down by 60 dB.

For the purposes of this problem, the ﬁlter’s phase response may be ignored in deter-

mining the output

y(t). Does this ﬁlter help in removing the aliased components?

What happens if the ﬁlter’s attenuation rate is reduced to 30 dB/octave?

Solution: The six terms of x(t) have frequencies:

20 1. SAMPLING AND RECONSTRUCTION

= 5 kHz

= 15 kHz

= 25 kHz

= 30 kHz

= 45 kHz

= 62.5 kHz

Only

and f

are audible; the rest are inaudible. Our ears ﬁlter out all frequencies beyond

20 kHz, and we hear

x(t) as though it were the signal:

(t)= 2A cos(10πt)+2B cos(30πt)

Each term of x(t) is represented in the frequency domain by two peaks at positive and

negative frequencies, for example, the

A-term has spectrum:

A cos(2πf

t)= Ae

2πjf

+ Ae

−2πjf

−→ A δ(f − f

)+A δ(f + f

)

Therefore, the spectrum of the input x(t) will be as shown below:

20-20 305070-30 10-10 40-40 60-60-70 -50 kHz

Nyquist

interval

ideal prefilter

AACCEFEFBBDD

The sampling process will replicate each of these peaks at multiples of f

= 40 kHz. The

four terms

C, D, E, F lie outside the [−20, 20] kHz Nyquist interval and therefore will be

aliased with the following frequencies inside the interval:

= 25 ⇒ f

C, a

= f

mod (f

)= f

− f

= 25 − 40 =−15

= 30 ⇒ f

D, a

= f

mod (f

)= f

− f

= 30 − 40 =−10

= 45 ⇒ f

E, a

= f

mod (f

)= f

− f

= 45 − 40 = 5

= 62.5 ⇒ f

F, a

= f

mod (f

)= f

− 2f

= 62.5 − 2 × 40 =−17.5

In case (a), if we do not use any preﬁlter at all, we will have

y(t)= x(t) and the recon-

structed signal will be:

(t) = 2A cos(10πt)+2B cos(30πt)

2C cos(−2π15t)+2D cos(−2π10t)

2E cos(2π5t)+2F cos(−2π17.5t)

2(A + E)cos(10πt)+2(B + C)cos(30πt)

2D cos

(20πt)+2F cos(35πt)

1.4. SAMPLING OF SINUSOIDS 21

where we replaced each out-of-band frequency with its aliased self, for example,

C cos(2πf

t)→ 2C cos(2πf

C,a

The relative amplitudes of the 5 and 15 kHz audible components have changed and, in

addition, two new audible components at 10 and 17

.5 kHz have been introduced. Thus,

(t) will sound very different from x(t).

In case (b), if an ideal preﬁlter with cutoff

/2 = 20 kHz is used, then its output will be

the same as the audible part of

x(t), that is, y(t)= x

(t). The ﬁlter’s effect on the input

spectrum is to remove completely all components beyond the 20 kHz Nyquist frequency,

as shown below:

20-20 305070-30 10-10 40-40 60-60-70 -50 kHz

Nyquist

interval

ideal prefilter

CCEFEF

Because the preﬁlter’s output contains no frequencies beyond the Nyquist frequency, there

will be no aliasing and after reconstruction the output would sound the same as the input,

(t)= y(t)= x

(t).

In case (c), if the practical preﬁlter

H(f) is used, then its output y(t) will be:

y(t) = 2A|H(f

)|cos(10πt)+2B|H(f

)|cos(30πt)

2C|H(f

)|cos(50πt)+2D|H(f

)|cos(60πt)

2E|H(f

)|cos(90πt)+2F|H(f

)|cos(125πt)

(1.4.7)

This follows from the steady-state sinusoidal response of a ﬁlter applied to the individual

sinusoidal terms of

x(t), for example, the effect of H(f) on A is:

A cos(2πf

−→

2A|H(f

)|cos



2πf

t + θ(f

)



where in Eq. (1.4.7) we ignored the phase response θ(f

)= arg H(f

). The basic conclu-

sions of this example are not affected by this simpliﬁcation.

Note that Eq. (1.4.7) applies also to cases (a) and (b). In case (a), we can replace:

|H(f

)|=|H(f

)|=1

and in case (b):

|H(f

)|=|H(f

)|=1, |H(f

)|=|H(f

)|=0

22 1. SAMPLING AND RECONSTRUCTION

In case (c), because f

and f

are in the ﬁlter’s passband, we still have

|H(f

)|=|H(f

)|=1

To determine

|H(f

)|, |H(f

)|, we must ﬁnd how many octaves

†

away

the frequencies

are from the f

/2 = 20 kHz edge of the passband. These are

given by:

log





log





0.322

log





log





0.585

log





log





1.170

log





log



62.5



1.644

and therefore, the corresponding ﬁlter attenuations will be:

: 60 dB/octave

× 0.322 octaves = 19.3dB

: 60 dB/octave × 0.585 octaves

= 35.1dB

: 60 dB/octave × 1.170 octaves

= 70.1dB

: 60 dB/octave

× 1.644 octaves = 98.6dB

By deﬁnition, an amount of

A dB attenuation corresponds to reducing |H(f)| by a factor

−A/20

. For example, the relative drop of |H(f)| with respect to the edge of the passband

|H(f

/2)| is A dB if:

|H(f)|

|H(f

/2)|

= 10

−A/20

Assuming that the passband has 0 dB normalization, |H(f

/2)|=1, we ﬁnd the following

values for the ﬁlter responses:

|H(f

)|=10

−19.3/20

|H(f

)|=10

−35.1/20

|H(f

)|=10

−70.1/20

3234

|H(f

)|=10

−98.6/20

85114

It follows from Eq. (1.4.7) that the output

y(t) of the preﬁlter will be:

†

The number of octaves is the number of powers of two, that is, if f

= 2

⇒ ν = log

1.4. SAMPLING OF SINUSOIDS 23

y(t) = 2A cos(10πt)+2B cos(30πt)

cos

(50πt)+

cos

(60πt)

3234

cos

(90πt)+

85114

cos

(125πt)

(1.4.8)

Its spectrum is shown below:

20-20 305070-30 10-10 40-40 60-60-70 -50 kHz

Nyquist

interval

(-19 dB)

(-35 dB)

(-70 dB)

(-98 dB)

Notice how the inaudible out-of-band components have been attenuated by the preﬁlter,

so that when they get aliased back into the Nyquist interval because of sampling, their

distorting effect will be much less. The wrapping of frequencies into the Nyquist interval

is the same as in case (a). Therefore, after sampling and reconstruction we will get:

(t) = 2



A +

3234



cos(10πt)+2



B +



cos(30πt)

cos

(20πt)+

85114

cos

(35πt)

Now, all aliased components have been reduced in magnitude. The component closest

to the Nyquist frequency, namely

, causes the most distortion because it does not get

attenuated much by the ﬁlter.

We will see in Section 1.5.3 that the preﬁlter’s rate of attenuation in dB/octave is related

to the ﬁlter’s order

N by α = 6N so that α = 60 dB/octave corresponds to 60 = 6N or

N = 10. Therefore, the given ﬁlter is already a fairly complex analog ﬁlter. Decreasing the

ﬁlter’s complexity to

α = 30 dB/octave, corresponding to ﬁlter order N = 5, would reduce

all the attenuations by half, that is,

: 30 dB/octave × 0.322 octaves = 9.7dB

: 30 dB/octave × 0.585 octaves = 17.6dB

: 30 dB/octave × 1.170 octaves = 35.1dB

: 30 dB/octave × 1.644 octaves = 49.3dB

and, in absolute units:

24 1. SAMPLING AND RECONSTRUCTION

|H(f

)|=10

−9.7/20

|H(f

)|=10

−17.6/20

7.5

|H(f

)|=10

−35.1/20

|H(f

)|=10

−49.3/20

292

Therefore, the resulting signal after reconstruction would be:

(t) = 2



A +



cos(10πt)+2



B +



cos(30πt)

7.5

cos

(20πt)+

292

cos

(35πt)

(1.4.9)

Now the

C and D terms are not as small and aliasing would still be signiﬁcant. The situation

can be remedied by oversampling, as discussed in the next example.



Example 1.4.8: Oversampling can be used to reduce the attenuation requirements of the pre-

ﬁlter, and thus its order. Oversampling increases the gap between spectral replicas reduc-

ing aliasing and allowing less sharp cutoffs for the preﬁlter.

For the previous example, if we oversample by a factor of 2,

= 2 × 40 = 80 kHz, the

new Nyquist interval will be

[−40, 40] kHz. Only the f

= 45 kHz and f

= 62.5 kHz

components lie outside this interval, and they will be aliased with

E,a

= f

− f

= 45 − 80 =−35 kHz

F,a

= f

− f

= 62.5 − 80 =−17.5 kHz

Only

F,a

lies in the audio band and will cause distortions, unless we attenuate f

using a

preﬁlter before it gets wrapped into the audio band. Without a preﬁlter, the reconstructed

signal will be:

(t) = 2A cos(10πt)+2B cos

(30πt)

2C cos(50πt)+2D cos

(60πt)

2E cos

(−2π35t)+2F cos(−2π17.5t)

2A cos(10πt)+2B cos(30πt)

2C cos(50πt)+2D cos(60πt)+2E cos(70πt)+2F cos(35πt)

The audible components in y

(t) are:

(t)= 2A cos(10πt)+2B cos(30πt)+2F cos(35πt)

Thus, oversampling eliminated almost all the aliasing from the desired audio band. Note

that two types of aliasing took place here, namely, the aliasing of the

E component which

1.4. SAMPLING OF SINUSOIDS 25

remained outside the relevant audio band, and the aliasing of the F component which does

represent distortion in the audio band.

Of course, one would not want to feed the signal

(t) into an ampliﬁer/speaker system

because the high frequencies beyond the audio band might damage the system or cause

nonlinearities. (But even if they were ﬁltered out, the

F component would still be there.)



Example 1.4.9: Oversampling and Decimation. Example 1.4.8 assumed that sampling at 80 kHz

could be maintained throughout the digital processing stages up to reconstruction. There

are applications however, where the sampling rate must eventually be dropped down to

its original value. This is the case, for example, in digital audio, where the rate must be

reduced eventually to the standardized value of 44.1 kHz (for CDs) or 48 kHz (for DATs).

When the sampling rate is dropped, one must make sure that aliasing will not be reintro-

duced. In our example, if the rate is reduced back to 40 kHz, the

C and D components,

which were inside the

[−40, 40] kHz Nyquist interval with respect to the 80 kHz rate,

would ﬁnd themselves outside the

[−20, 20] kHz Nyquist interval with respect to the 40

kHz rate, and therefore would be aliased inside that interval, as in Example 1.4.7.

To prevent

C and D, as well as E, from getting aliased into the audio band, one must

remove them by a lowpass digital ﬁlter before the sampling rate is dropped to 40 kHz.

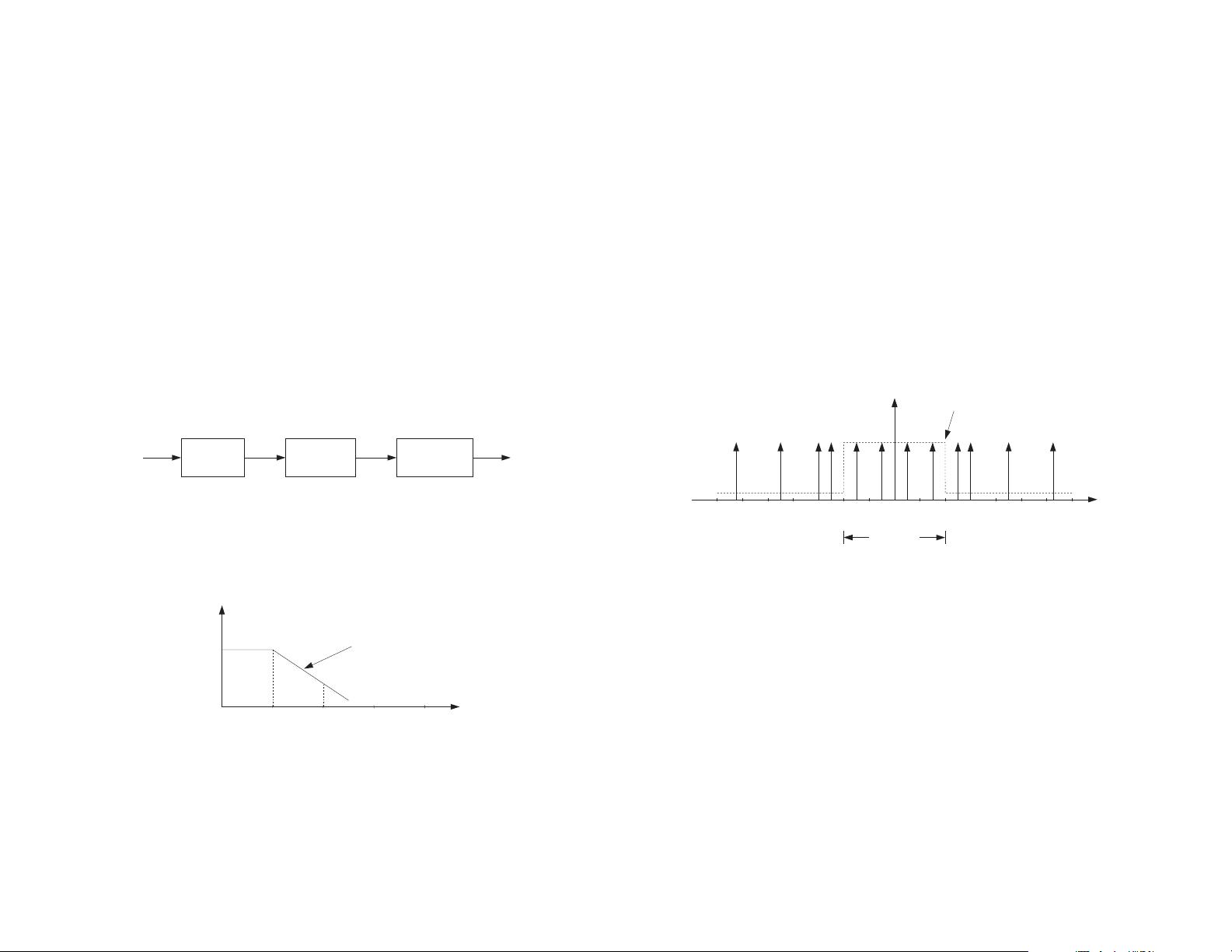
Such a ﬁlter is called a digital decimation ﬁlter. The overall system is shown below.

prefilter

H(f)

80 kHz

sampler

kHz

digital

filter

down-

sampler

recon-

structor

x(t)

y(t) y

(t)

analoganalog

The downsampler in this diagram reduces the sampling rate from 80 down to 40 kHz by

throwing away every other sample, thus, keeping only half the samples. This is equivalent

to sampling at a 40 kHz rate.

The input to the digital ﬁlter is the sampled spectrum of

y(t), which is replicated at mul-

tiples of 80 kHz as shown below.

20 30 50 70 9010 40 60 80 100 120 140 160 kHz

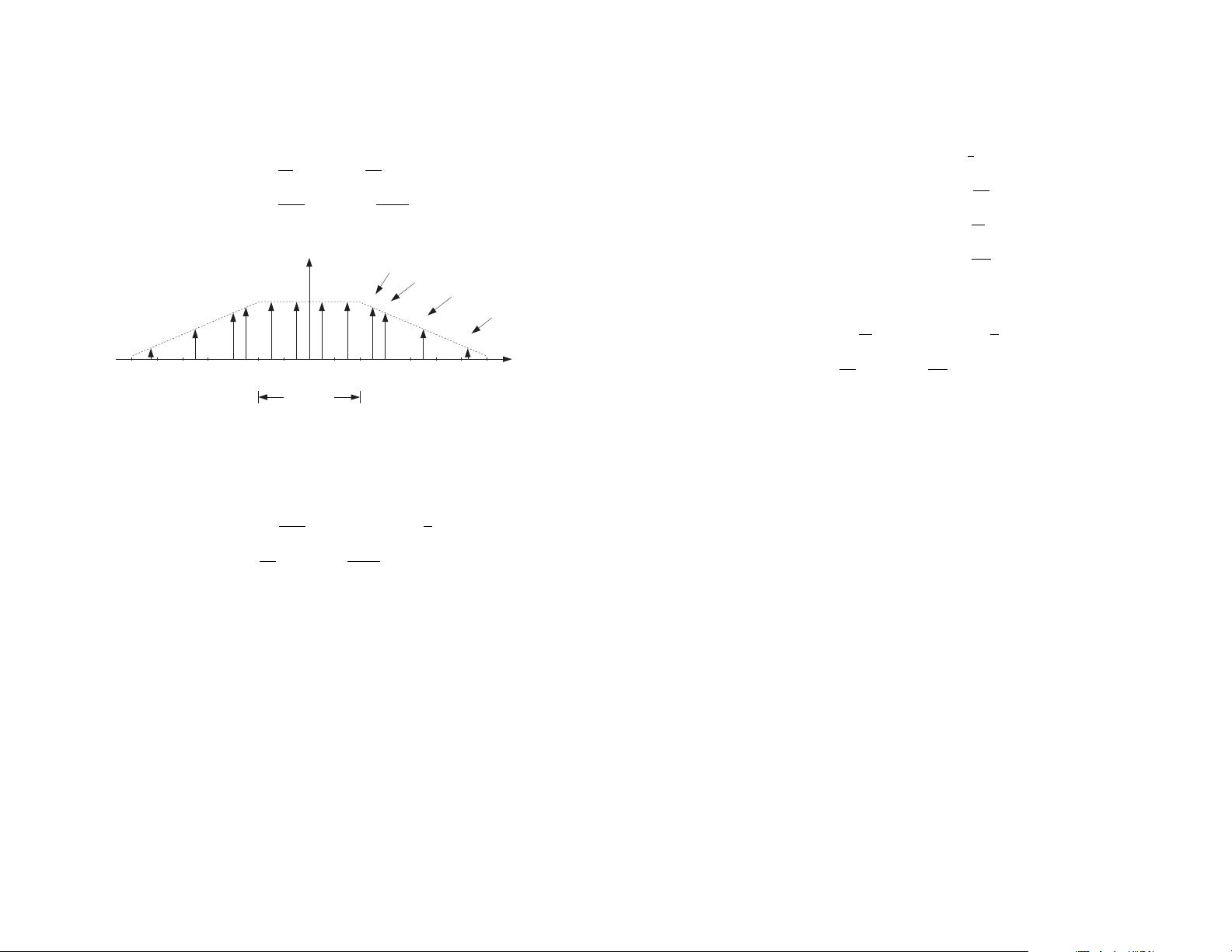
digital lowpass filter

prefilter

AAAA

CCCC

EEEE

FFFF

BBBB

DDDD

We have also assumed that the 30 dB/octave preﬁlter is present. The output of the digital

ﬁlter will have spectrum as shown below.

26 1. SAMPLING AND RECONSTRUCTION

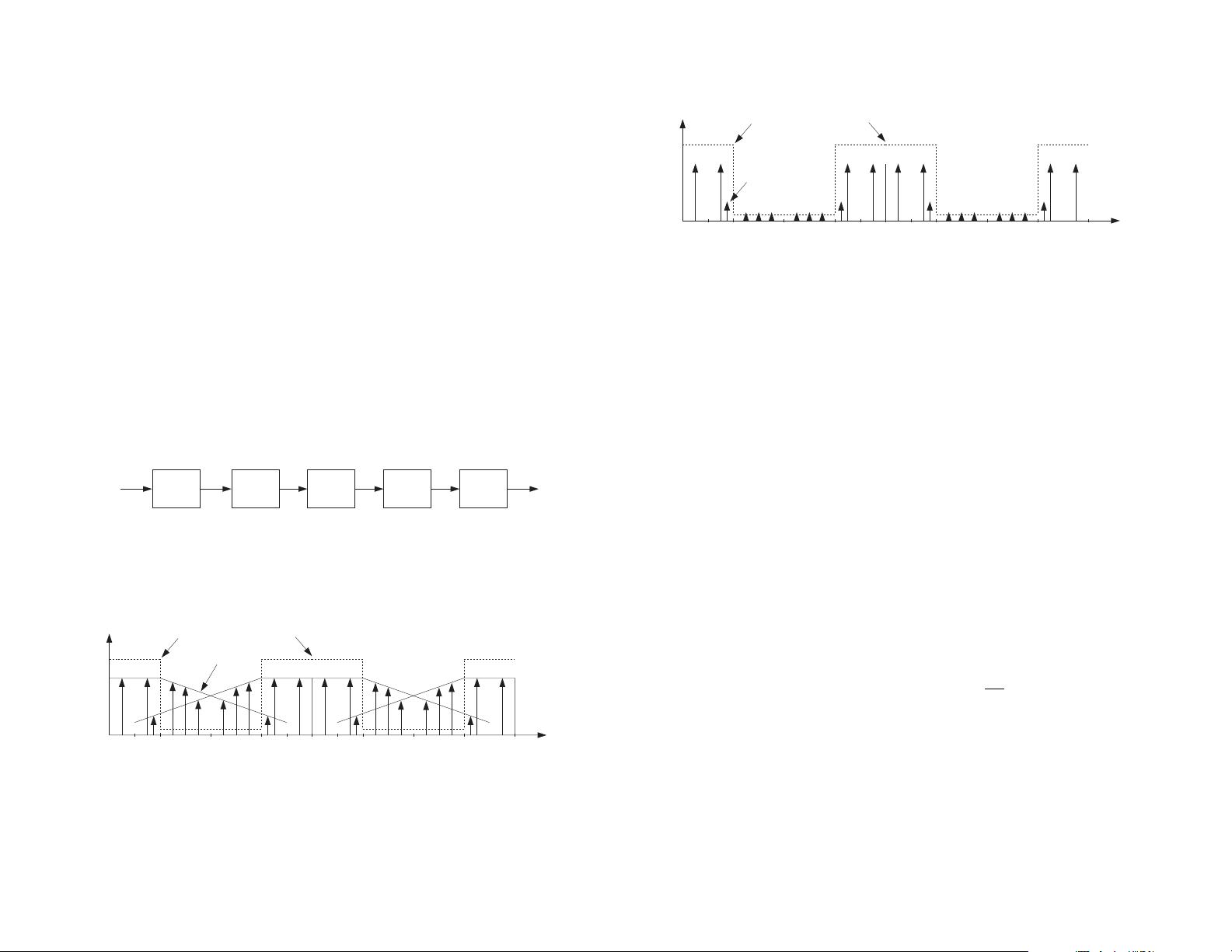
20 30 50 70 9010 40 60 80 100 120 140 160 kHz

digital lowpass filter

AAAA

FFFF

BBBB

CCEEDD C CEEDD

(-49 dB)

The digital ﬁlter operates at the oversampled rate of 80 kHz and acts as a lowpass ﬁlter

within the

[−40, 40] kHz Nyquist interval, with a cutoff of 20 kHz. Thus, it will remove the

C, D, and E components, as well as any other component that lies between 20 ≤|f|≤60

kHz.

However, because the digital ﬁlter is periodic in

f with period f

= 80 kHz, it cannot remove

any components from the interval 60

≤ f ≤ 100. Any components of the analog input y(t)

that lie in that interval would be aliased into the interval 60 −80 ≤ f −f

≤ 100−80, which

is the desired audio band

−20 ≤ f − f

≤ 20. This is what happened to the F component,

as can be seen in the above ﬁgure.

The frequency components of

y(t) in 60 ≤|f|≤100 can be removed only by a pre-

ﬁlter, prior to sampling and replicating the spectrum. For example, our low-complexity

30 dB/octave preﬁlter would provide 47.6 dB attenuation at 60 kHz. Indeed, the number

of octaves from 20 to 60 kHz is log

(60/20)= 1.585 and the attenuation there will be

30 dB/octave

× 1.584 octaves = 47.6 dB.

The preﬁlter, being monotonic beyond 60 kHz, would suppress all potential aliased compo-

nents beyond 60 kHz by more than 47.6 dB. At 100 kHz, it would provide 30

×log

(100/20)=

69.7 dB attenuation. At f

= 62.5 kHz, it provides 49.3 dB suppression, as was calculated

in Example 1.4.7, that is,

|H(f

)|=10

−49.3/20

= 1/292.

Therefore, assuming that the digital ﬁlter has already removed the

C, D, and E compo-

nents, and that the aliased

F component has been sufﬁciently attenuated by the preﬁlter,

we can now drop the sampling rate down to 40 kHz.

At the reduced 40 kHz rate, if we use an ideal reconstructor, it would extract only the

components within the

[−20, 20] kHz band and the resulting reconstructed output will

be:

(t)= 2A cos

(10πt)+2B cos(30πt)+

292

cos

(35πt)

which has a much attenuated aliased component F. This is to be compared with Eq. (1.4.9),

which used the same preﬁlter but no oversampling. Oversampling in conjunction with

digital decimation helped eliminate the most severe aliased components,

C and D.

In summary, with oversampling, the complexity of the analog preﬁlter can be reduced and

traded off for the complexity of a digital ﬁlter which is much easier to design and cheaper

to implement with programmable DSPs. As we will see in Chapter 2, another beneﬁt of

oversampling is to reduce the number of bits representing each quantized sample. The

connection between sampling rate and the savings in bits is discussed in Section 2.2. The

subject of oversampling, decimation, interpolation, and the design and implementation of

digital decimation and interpolation ﬁlters will be discussed in detail in Chapter 12.



1.4. SAMPLING OF SINUSOIDS 27

1.4.2 Rotational Motion

A more intuitive way to understand the sampling properties of sinusoids is to consider a

representation of the complex sinusoid

x(t)= e

2πjf t

as a wheel rotating with a frequency

f revolutions per second. The wheel is seen in a dark room by means of a strobe light

ﬂashing at a rate of

ﬂashes per second. The rotational frequency in [radians/sec] is

Ω = 2πf . During the time interval T between ﬂashes, the wheel turns by an angle:

ω = ΩT = 2πf T =

2πf

(1.4.10)

This quantity is called the digital frequency and is measured in units of [radians/sample].

It represents a convenient normalization of the physical frequency

f. In terms of ω, the

sampled sinusoid reads simply

x(nT)= e

2πjf Tn

= e

jωn

In units of ω, the Nyquist frequency f = f

/2 becomes ω = π and the Nyquist interval

becomes

[−π, π]. The replicated set f + mf

becomes

π(f +mf

)

2πf

+ 2πm = ω + 2πm

Because the frequency f = f

corresponds to ω = 2π, the aliased frequency given in

Eq. (1.4.3) becomes in units of

ω:

= ω mod(2π)

The quantity f/f

= fT is also called the digital frequency and is measured in units

of [cycles/sample]. It represents another convenient normalization of the physical fre-

quency axis, with the Nyquist interval corresponding to

[−0.5, 0.5].

In terms of the rotating wheel,

fT represents the number of revolutions turned dur-

ing the ﬂashing interval

T. If the wheel were actually turning at the higher frequency

f +mf

, then during time T it would turn by (f +mf

)T = fT+mf

T = fT+m revo-

lutions, that is, it would cover

m whole additional revolutions. An observer would miss

these extra

m revolutions completely. The perceived rotational speed for an observer is

always given by

= f mod(f

). The next two examples illustrate these remarks.

Example 1.4.10:

Consider two wheels turning clockwise, one at f

= 1 Hz and the other at

= 5 Hz, as shown below. Both are sampled with a strobe light ﬂashing at f

= 4 Hz.

Note that the second one is turning at

= f

+ f

n=0 n=0

n=1 n=1

n=2 n=2

n=3 n=3

f=1 f=5

ω=π/2

ω=5π/2

=π/2

28 1. SAMPLING AND RECONSTRUCTION

The ﬁrst wheel covers f

T = f

= 1/4 of a revolution during T = 1/4 second. Its angle

of rotation during that time interval is

= 2πf

= 2π/4 = π/2 radians. During the

sampled motion, an observer would observe the sequence of points

n = 0, 1, 2, 3,... and

would conclude that the wheel is turning at a speed of 1/4 of a revolution in 1/4 second,

or,

/4 cycles

1/4 sec

= 1Hz

Thus, the observer would perceive the correct speed and sense of rotation. The second

wheel, on the other hand, is actually turning by

T = f

= 5/4 revolutions in 1/4

second, with an angle of rotation

= 5π/2. Thus, it covers one whole extra revolution

compared to the ﬁrst one. However, the observer would still observe the same sequence

of points

n = 0, 1, 2, 3,..., and would conclude again that the wheel is turning at 1/4

revolution in 1/4 second, or, 1 Hz. This result can be obtained quickly using Eq. (1.4.3):

= f

mod(f

)= 5 mod(4)= 5 − 4 = 1

Thus, in this case the perceived speed is wrong, but the sense of rotation is still correct.

In the next ﬁgure, we see two more wheels, one turning clockwise at

= 9 Hz and the

other counterclockwise at

=−3 Hz.

n=0 n=0

n=1 n=1

n=2 n=2

n=3 n=3

f=9 f=−3

ω=9π/2

ω=−

π/2

=π/2

The negative sign signiﬁes here the sense of rotation. During T = 1/4 sec, the third wheel

covers

T = 9/4 revolutions, that is, two whole extra revolutions over the f

wheel. An

observer would again see the sequence of points

n = 0, 1, 2, 3,..., and would conclude

that

is turning at 1 Hz. Again, we can quickly compute, f

= f

mod(f

)= 9 mod(4)=

9 − 2 · 4 = 1 Hz.

The fourth wheel is more interesting. It covers

T =−3/4 of a revolution in the coun-

terclockwise direction. An observer captures the motion every 3/4 of a counterclockwise

revolution. Thus, she will see the sequence of points

n = 0, 1, 2, 3,..., arriving at the

conclusion that the wheel is turning at 1 Hz in the clockwise direction. In this case, both

the perceived speed and sense of rotation are wrong. Again, the same conclusion can be

reached quickly using

= f

mod(f

)= (−3) mod(4)=−3 + 4 = 1 Hz. Here, we added

one

in order to bring f

within the Nyquist interval [−2, 2]. 

Example 1.4.11:

The following ﬁgure shows four wheels rotating clockwise at f = 1.5, 2, 2.5, 4

Hz and sampled at

= 4 Hz by a strobe light.

剩余397页未读，继续阅读

halfac_y

粉丝: 0
资源: 1

《信号处理基础》Sophocles J. Orfanidis-数字信号处理概论

信号处理导论：Sophocles J. Orfanidis经典教程解析

信号处理基础：Orfanidis的导论

Optimum Signal Processing: An Introduction

Introduction To signal Processing--Sophocles J.Orfanidis信号处理导论

信号处理导论（Sophocles J. Orfanidis） 参考答案

Optimum Signal Processing An introduction

Optimum Signal Processing

3 波段参数均衡器：由用户友好的 GUI 控制的 3 波段参数均衡器的 Simulink 模型。-matlab开发

信号处理基础概论

基于 .NET 5 + Ant Design Vue 的 Admin Fx.zip

最新资源

信号处理导论（Sophocles J. Orfanidis）参考答案