单片机原理：第2章 数制转换与数据格式

"这篇文档是关于单片机原理及应用的第二章，主要讲解了单片机中常用的数制、编码及数据格式。内容涵盖了数制间的转换、二进制运算以及计算机中数字的表示方法。" 在计算机科学，尤其是单片机技术中，理解和掌握各种数制是非常基础且重要的。数制是表示数值的不同方式，常见的有十进制、二进制、八进制和十六进制。十进制是我们日常生活中最常用的数制，它有10个不同的数字字符：0到9。在电子电路设计中，由于二进制更容易实现，因此在计算机系统中广泛使用。 2.1.1 十进制数制 十进制是一种基于10的计数系统，其中每一位的数值是前一位的10倍。例如，数字345.56的每一位都对应着一个特定的权重，从左到右分别为300、40、5、0.5和0.06。在十进制中，每增加一位，位权就增加10倍。这意味着一个N位的十进制数能表示从0到10的N次方减1的所有整数。 2.1.2 十进制计数 在十进制计数中，每一位按照"逢十进一"的规则递增。例如，个位从0到9变化，每满10就进一位到十位，十位再从0开始，以此类推。这种计数方式在日常生活和计算中直观易懂。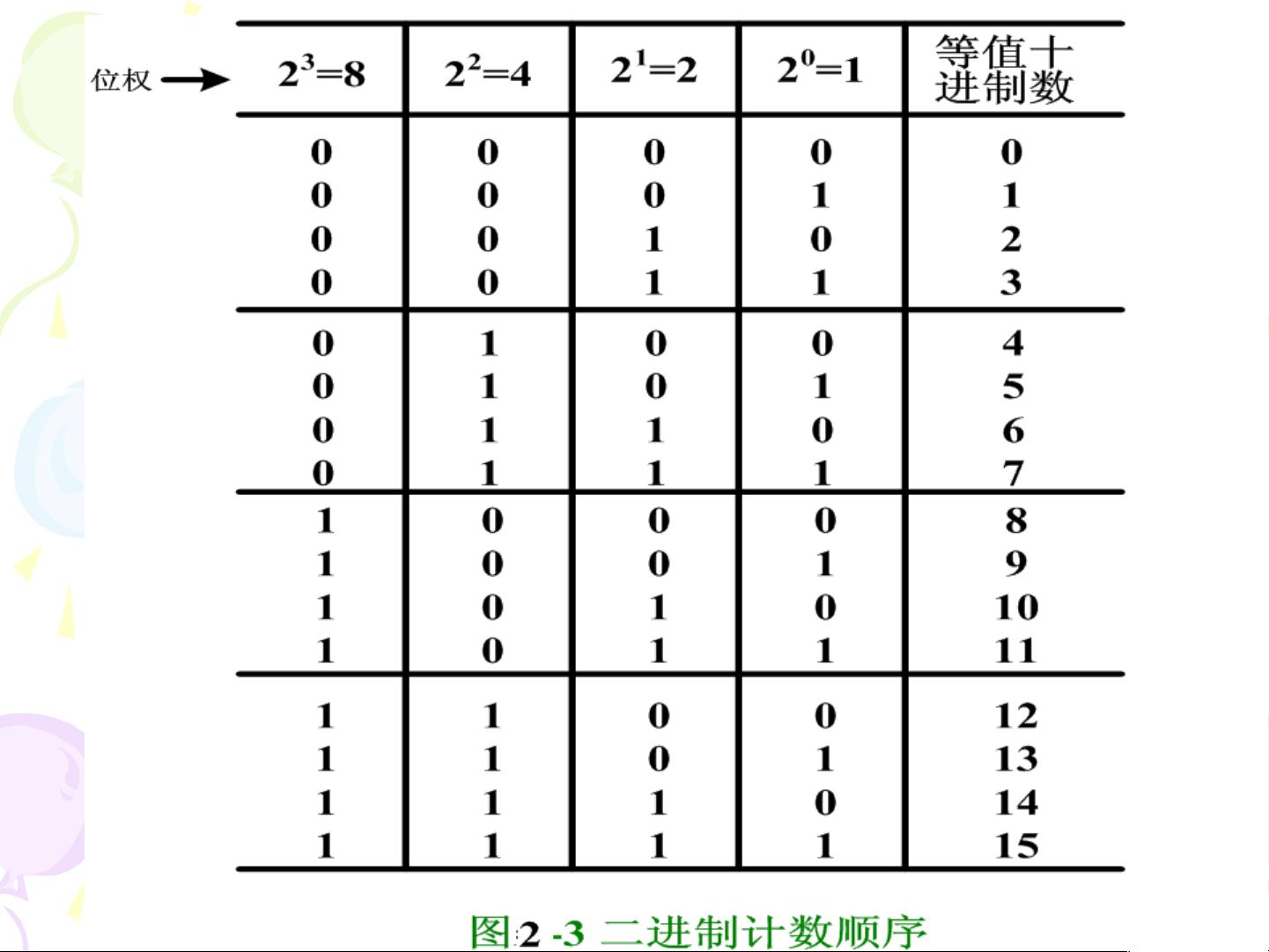 2.1.3 二进制数制 二进制数制仅有两个符号：0和1。虽然表示一个数所需的位数相对较多，但它的简单性使得在电子设备中容易实现。二进制的进位规则是"逢二进一"。比如，二进制数1011表示十进制中的11，因为1×2^3 + 0×2^2 + 1×2^1 + 1×2^0 = 8 + 0 + 2 + 1 = 11。 2.2 数制之间的转换 转换数制是编程和计算机处理数据时的常见操作。例如，将十进制数转换为二进制，通常采用除二取余法；而将二进制转换为十进制，可以使用按位权重累加的方法。 2.3 二进制数的运算 二进制数的运算包括加法、减法、乘法和除法，它们遵循与十进制类似的规则，只是在二进制下进行。例如，二进制加法遵循"0+0=0，0+1=1，1+0=1，1+1=10"的规则，"10"表示进位。 2.4 计算机中数的表示方法 在计算机内部，所有的数据都是以二进制形式存储和处理的。这包括正负数、浮点数以及各种编码形式，如原码、反码、补码用于表示有符号整数，IEEE 754标准用于表示浮点数。理解这些表示方法对于编写有效的单片机程序至关重要。 本章内容是学习单片机原理和程序设计的基础，对数制的理解有助于深入学习后续的指令集、内存管理、I/O接口等概念。