基于Canvas使用贝塞尔曲线平滑拟合折线段的方法详解

基于Canvas使用贝塞尔曲线平滑拟合折线段的方法 **贝塞尔曲线的概念** 贝塞尔曲线是一种数学曲线，用于描述平滑曲线的形状。它由法国工程师Pierre Bézier在1960年代提出，主要应用于计算机图形学和计算机辅助设计领域。贝塞尔曲线的特点是可以通过多个控制点来调整曲线的形状，使其变得更加平滑和自然。 **贝塞尔曲线在Canvas中的应用** 在Canvas中，我们可以使用贝塞尔曲线来平滑拟合折线段，实现更加自然和平滑的曲线效果。通过使用贝塞尔曲线，我们可以将折线段的棱角“磨平”，使其变得更加圆润和自然。 **为什么要平滑拟合折线段** 在数据可视化领域，折线图是最常见的一种图表类型。然而，折线图的棱角部分往往会使图表看起来不够平滑和自然。这时，我们可以使用贝塞尔曲线来平滑拟合折线段，实现更加平滑和自然的曲线效果。贝塞尔曲线可以帮助我们实现更加高质量的数据可视化效果。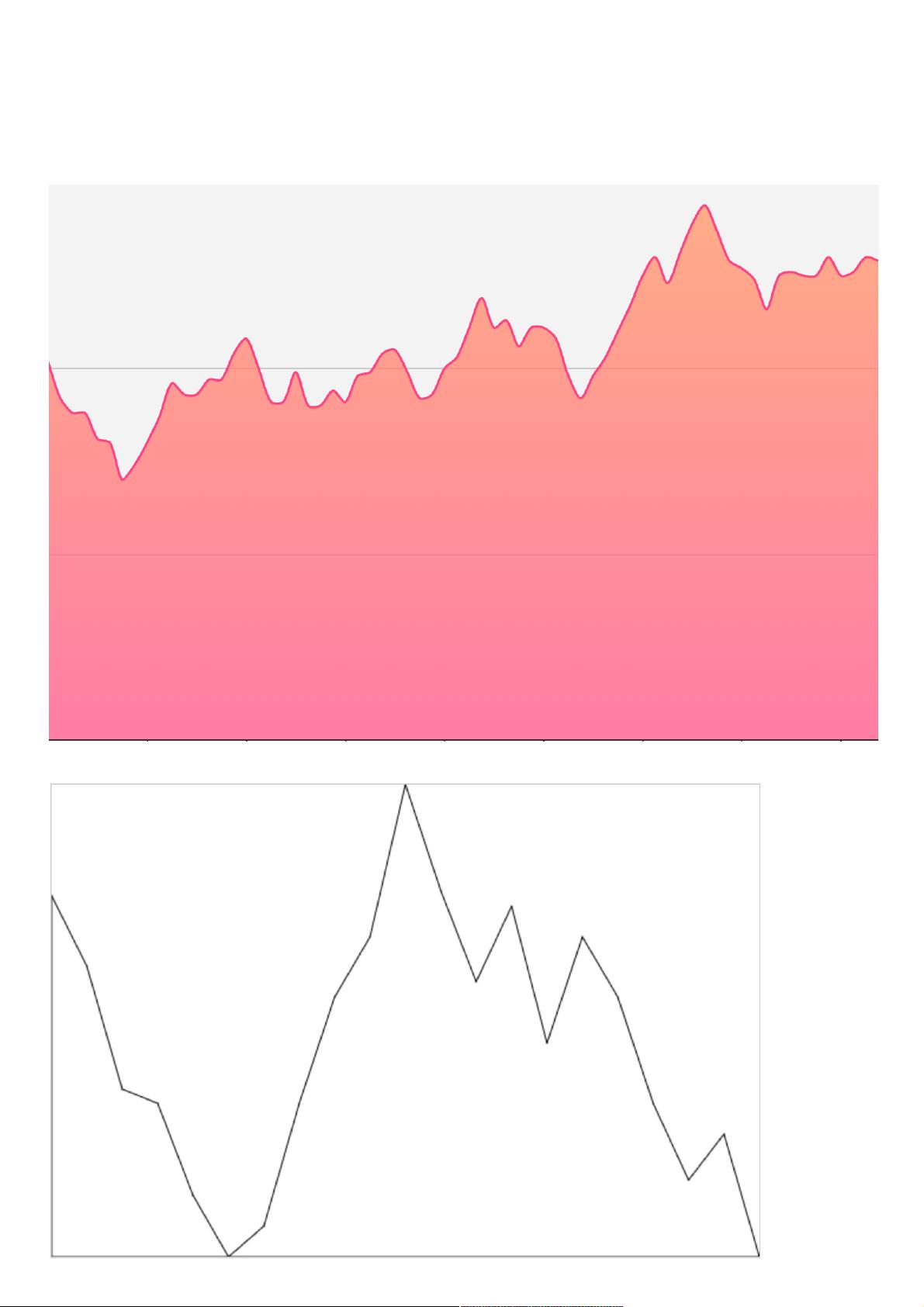 **实现贝塞尔曲线平滑拟合折线段的步骤** 要实现贝塞尔曲线平滑拟合折线段，我们需要按照以下步骤进行： 1. 绘制折线图：首先，我们需要绘制一个基本的折线图，包括折线段的所有描点。 2. 贝塞尔曲线平滑拟合：然后，我们可以使用贝塞尔曲线来平滑拟合折线段，实现更加平滑和自然的曲线效果。 **模拟数据** 在本例中，我们使用了模拟数据来生成折线图。模拟数据是通过随机数生成的，模拟了真实数据的变化趋势。 **实现贝塞尔曲线平滑拟合的代码** 在实现贝塞尔曲线平滑拟合时，我们可以使用JavaScript语言来编写代码。首先，我们需要初始化一个构造函数来放置需要用到的数据，然后我们可以使用贝塞尔曲线来平滑拟合折线段。下面是一个简单的示例代码： ``` function LinearGradient(option) { this.canvas = document.getElementById(option.canvas.id); this.ctx = this.canvas.getContext('2d'); this.width = this.canvas.width; this.height = this.canvas.height; this.tooltip = option.tooltip; this.title = option.text; this.series = [...]; } ``` **总结** 贝塞尔曲线平滑拟合折线段是数据可视化领域中的一种重要技术。通过使用贝塞尔曲线，我们可以实现更加平滑和自然的曲线效果，提高数据可视化的质量。在本文中，我们介绍了贝塞尔曲线的概念、贝塞尔曲线在Canvas中的应用、为什么要平滑拟合折线段、实现贝塞尔曲线平滑拟合折线段的步骤、模拟数据和实现贝塞尔曲线平滑拟合的代码。