RMQ与LCA算法详解:从基础到优化
需积分: 22 154 浏览量
更新于2024-07-19
收藏 680KB PDF 举报
"本文主要介绍了RMQ(Range Minimum/Maximum Query)问题和LCA(Lowest Common Ancestor)问题,并探讨了如何解决这两个问题的算法,包括ST算法和Tarjan离线算法。同时,提到了RMQ和LCA在字符串处理、生物学计算以及信息学竞赛中的应用。"
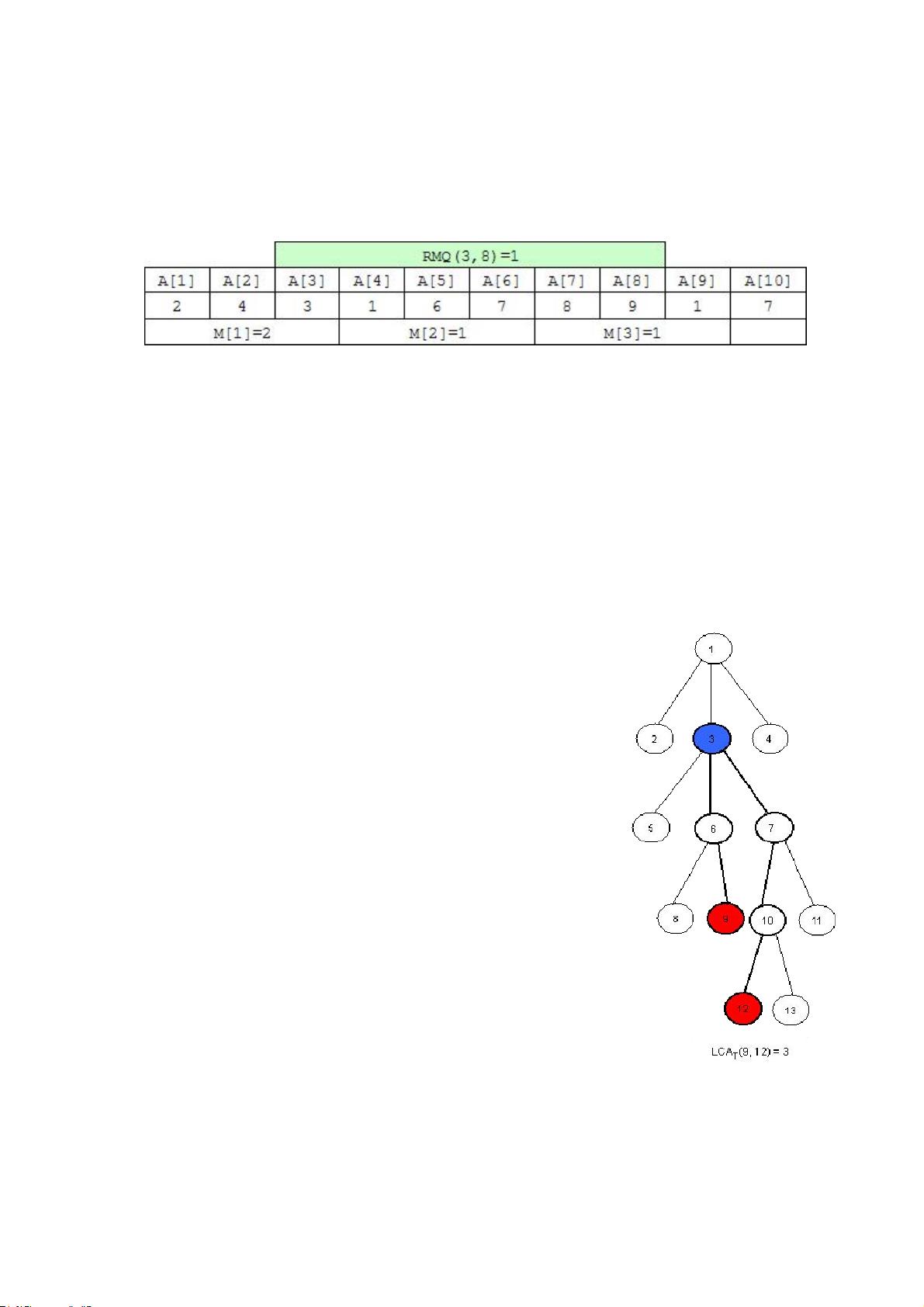
在计算机科学和算法设计中,RMQ和LCA是两个非常重要的概念。RMQ问题通常涉及在一个数组或序列中,给定两个索引,快速找到它们之间(包含这两个索引)的最小值或最大值。最直观的方法是线性扫描,但这种方法在大量查询的情况下效率低下。线段树是一种常用的解决RMQ的结构,它的预处理时间为O(n),查询时间为O(log n)。然而,Sparse Table(ST)算法提供了更优的解决方案,预处理时间同样为O(n log n),但在查询时能达到O(1)的效率。
ST算法的预处理阶段是通过动态规划实现的。定义f(i, j)表示从第i个元素开始,连续2^j个元素中的最小值。利用这个定义,可以自底向上计算出所有f(i, j)的值。状态转移方程是基于f(i, j)可以由f(i, j-1)和f(i+2^(j-1), j-1)推导出来,初始状态f(i, 0)等于数组中的第i个元素。
LCA问题则是关于树的数据结构,寻找给定两个节点在树中的最近公共祖先。这个问题在图论和数据结构中有着广泛的应用,尤其是在生物学计算中,例如在分析基因进化树。Tarjan离线LCA算法是一种高效的解决方案,它允许一次性处理多个查询,从而降低了时间复杂度。
RMQ和LCA问题在信息学奥赛中常常出现,因此理解和掌握这两种问题的高效解法对于参赛者来说至关重要。它们还可以通过某些方式相互转换,例如通过构建特定的数据结构如笛卡尔树或使用欧拉序列,来结合解决RMQ和LCA问题。
此外,文章还提到了±1RMQ,这是一种扩展的RMQ问题,需要处理在区间内元素加减1的情况。并查集则是一种用于处理集合操作的数据结构,可能在解决某些与RMQ和LCA相关的复杂问题时发挥作用。
RMQ和LCA问题在实际应用中具有很高的价值,学习并熟练掌握相关算法不仅可以提高编程能力,也有助于解决实际工程中的效率问题。通过ST算法、Tarjan算法等工具,我们可以有效地处理这些问题,提高程序运行效率。
点击了解资源详情
167 浏览量
点击了解资源详情
258 浏览量
274 浏览量
150 浏览量
Simon_Bariona
- 粉丝: 317
最新资源
- 小学水墨风学校网站模板设计
- 深入理解线程池的实现原理与应用
- MSP430编程代码集锦:实用例程源码分享
- 绿色大图幻灯商务响应式企业网站开发源码包
- 深入理解CSS与Web标准的专业解决方案
- Qt/C++集成Google拼音输入法演示Demo
- Apache Hive 0.13.1 版本安装包详解
- 百度地图范围标注技术及应用
- 打造个性化的Windows 8锁屏体验
- Atlantis移动应用开发深度解析
- ASP.NET实验教程:源代码详细解析与实践
- 2012年工业观察杂志完整版
- 全国综合缴费营业厅系统11.5:一站式缴费与运营管理解决方案
- JAVA原生实现HTTP请求的简易指南
- 便携PDF浏览器:随时随地快速查看文档
- VTF格式图片编辑工具:深入起源引擎贴图修改