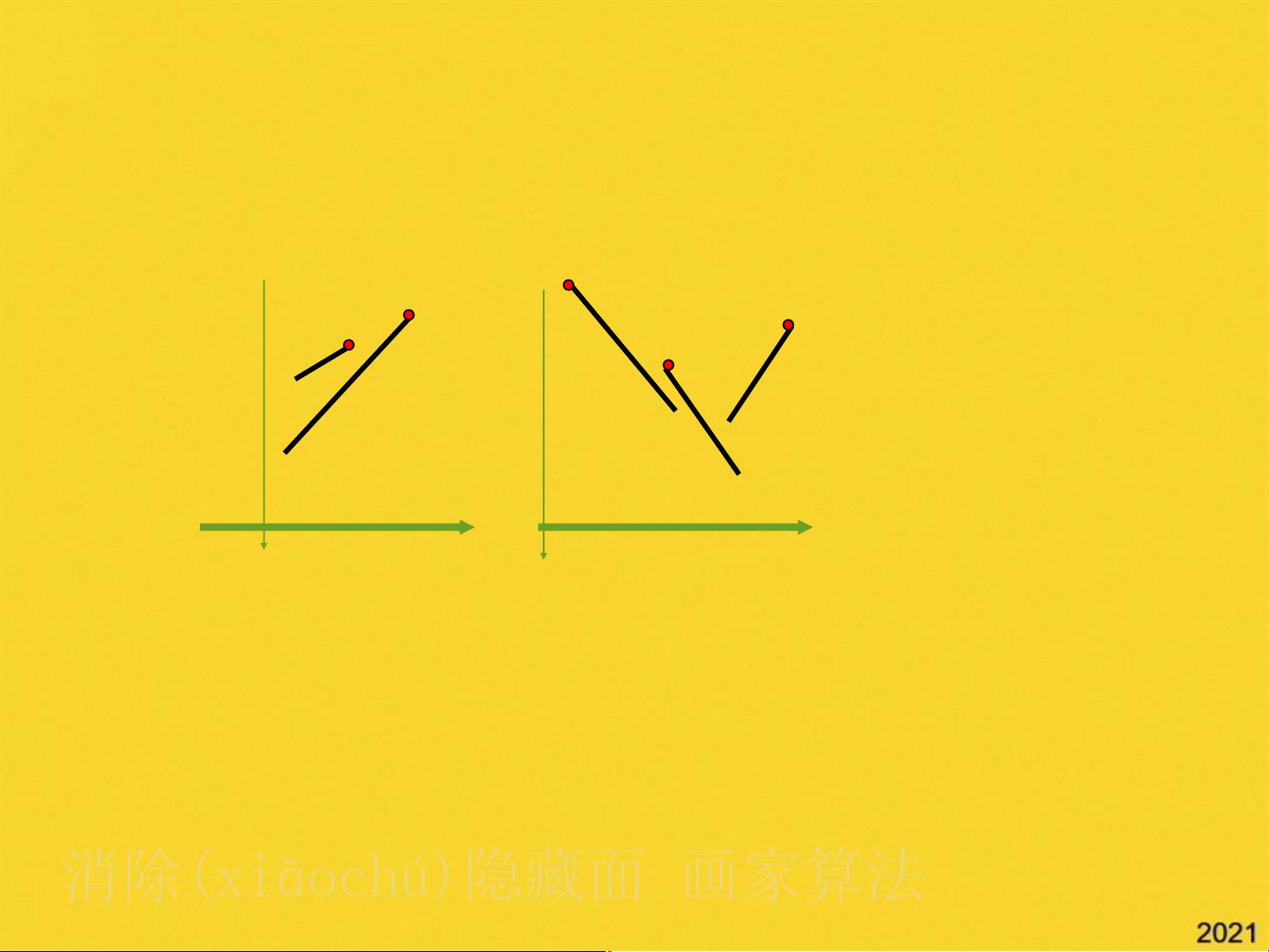深度优先:计算机图形学隐面算法详解及应用
29 浏览量
更新于2024-06-29
收藏 544KB PPT 举报
计算机图形学隐面算法是计算机图形学中的一个重要概念,主要用于在三维空间中消除物体上不可见的表面,确保最终在屏幕上显示的图像只包含可见部分。这些算法通常在绘制三维场景时被应用,目标是精确地决定每个像素的颜色和透明度。
1. 点取样算法:这是一种基本的隐面算法,它通过在投影面上选取一系列离散点,分析每个点对应物体表面的可见性,以此来决定像素的颜色和光照效果。
2. 画家算法:也称为深度优先渲染或深度排序算法,其核心思想是按照物体与观察者距离的远近顺序绘制。首先,将所有物体的面根据距离排序,从远处的背景开始绘制,逐渐接近物体,这样可以自然地体现出遮挡关系。这种算法依赖于深度优先级表,其中物体的优先级由其距离决定,远离观察点的物体先被处理。
- 深度优先级表的建立:构建深度优先级表时要考虑多边形的相对位置和投影重叠情况。对于简单的场景,可以确定优先级;复杂场景中,可能需要更复杂的判断规则,例如比较包围盒在不同坐标轴上的投影是否相交,或者考虑物体的前后顺序。
3. Z缓冲区算法:这是一种基于硬件加速的方法,利用一个单独的缓冲区存储每个像素的Z值,避免重复计算。当绘制新表面时,仅更新那些Z值更大的像素,从而减少计算量,提高渲染效率。
4. 扫描线算法:这种方法沿着屏幕的垂直线从左到右逐行处理,通过比较物体的边界与当前扫描线的关系,确定哪些部分是可见的。这种算法适合处理复杂形状和透明效果。
5. 区域采样算法:它是一种混合策略,通过划分场景区域并分别处理,结合了点取样和扫描线算法的优点,提高了处理大规模场景的效率。
计算机图形学的隐面算法是实现真实感三维渲染的关键技术,它们在游戏开发、动画制作、建筑设计等领域发挥着重要作用,确保了用户能够看到预期的、符合逻辑的三维视觉效果。理解这些算法的工作原理和优化策略对于深入学习计算机图形学至关重要。
2023-05-28 上传
2022-11-15 上传
2022-11-18 上传
2022-11-15 上传
2022-11-24 上传
2021-10-09 上传
2022-11-17 上传