"支持向量机II：非可分情况下的支持向量总结"

In the second part of the Support Vector Machine, the concept of support vectors in the non-separable case is discussed. Support vectors are defined as the training examples (x(i), y(i)) for which the corresponding α∗i is greater than 0. The KKT dual complementarity condition is also revisited, where α∗i gi(ω∗) = 0 and η∗i ξi = 0 are the key equations. This condition implies that if α∗i = 0, then y(i)(w∗Tx(i) - b) - 1 ξi = 0 and η∗i ξi = 0. 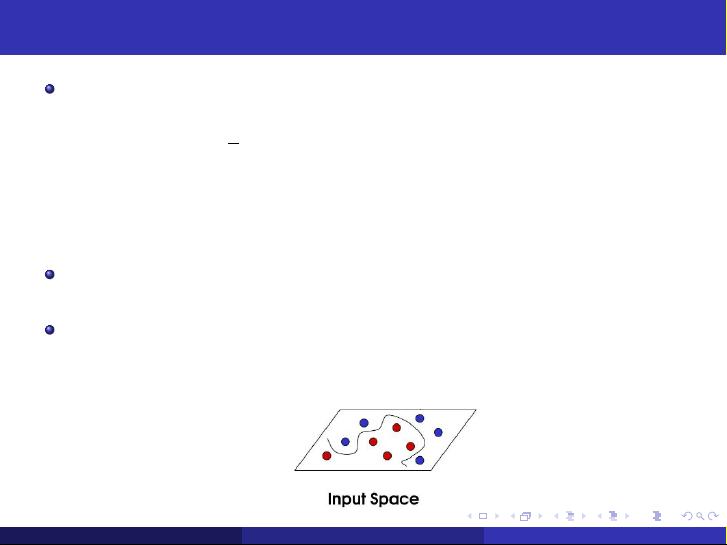Support vectors play a critical role in the SVM algorithm, especially in cases where the data is not linearly separable. These support vectors are the data points that lie closest to the decision boundary and have a non-zero α∗i value. By focusing on the support vectors, the SVM algorithm is able to effectively find the optimal hyperplane that maximizes the margin between classes. Overall, the understanding and identification of support vectors are essential in the successful implementation of Support Vector Machine in both separable and non-separable cases. By leveraging the support vectors and the KKT dual complementarity condition, the SVM algorithm is able to accurately classify data points and make predictions with high accuracy.